Drobiazgi
O tym, czego nie ma
Największa liczba pierwsza
Jeśli liczba naturalna
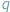 jest największą liczbą pierwszą, to...
jest największą liczbą pierwszą, to...
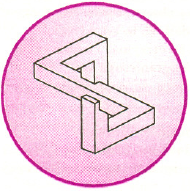
...istnieje liczb pierwszych tylko skończenie wiele – na pewno nie więcej
niż
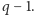 Można je więc wszystkie ponumerować, powiedzmy
Można je więc wszystkie ponumerować, powiedzmy
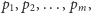 gdzie, oczywiście,
gdzie, oczywiście,
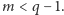
Liczba

ma paradoksalne własności. Jako większa od
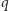 nie jest liczbą pierwszą,
jako liczba nie dzieląca się przez żadną z liczb
nie jest liczbą pierwszą,
jako liczba nie dzieląca się przez żadną z liczb
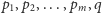 nie ma
dzielników naturalnych różnych od 1 i niej samej – jest więc pierwsza.
Dlatego też w jej definicji musiał zostać popełniony błąd. Ale jedynym
miejscem niepewnym jest założenie, że istnieje największa liczba pierwsza
– ono więc musi być fałszywe.
nie ma
dzielników naturalnych różnych od 1 i niej samej – jest więc pierwsza.
Dlatego też w jej definicji musiał zostać popełniony błąd. Ale jedynym
miejscem niepewnym jest założenie, że istnieje największa liczba pierwsza
– ono więc musi być fałszywe.
Jest to pierwsze historycznie spośród twierdzeń matematyki, które postulują, że czegoś jest nieskończenie wiele. Zostało udowodnione 2300 lat temu, najprawdopodobniej przez Euklidesa.
Mimo to, od czasu do czasu, prasa mniej lub bardziej naukowa donosi,
że największą liczbą pierwszą jest – żeby podać konkretny przykład
ze stycznia 1994 – liczba
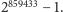 Rzecz jasna, chodzi tu o największą
liczbę pierwszą, jaką w danej chwili umielibyśmy konkretnie napisać
np. w układzie dziesiętnym. Poszukiwanie takich liczb to dobre zajęcie, bo – jak
widać – nigdy się nie skończy.
Rzecz jasna, chodzi tu o największą
liczbę pierwszą, jaką w danej chwili umielibyśmy konkretnie napisać
np. w układzie dziesiętnym. Poszukiwanie takich liczb to dobre zajęcie, bo – jak
widać – nigdy się nie skończy.