Anomalie kul i kostek
Kwadrat i koło mają swoje naturalne odpowiedniki trójwymiarowe (sześcian i kula), czterowymiarowe, pięciowymiarowe i dowolnie wymiarowe. Pisząc "dowolny wymiar", mamy na myśli więcej osi układu, czyli też współrzędnych opisujących obiekt. Wyobraźmy sobie mianowicie przestrzeń trójwymiarową (co nie jest specjalnie trudne). Każdy punkt takiej przestrzeni można opisać za pomocą zestawu trzech współrzędnych 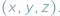 Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych
Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych 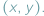 Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej
Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej 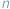 -wymiarową, używamy zestawu
-wymiarową, używamy zestawu 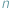 liczb
liczb 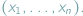
Potrzeba używania więcej niż trzech współrzędnych nie jest specjalnie wydumana. Wyobraźmy sobie, że chcemy opisać temperaturę w pomieszczeniu. Chcąc być absolutnie precyzyjnym, powinniśmy wskazać, jaka temperatura panuje w każdym jego punkcie (inna będzie nad kaloryferem, a inna w rogu pokoju). Czyli mamy 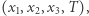 gdzie pierwsze trzy liczby to współrzędne punktu, a czwarta to temperatura. Chcąc opisać temperaturę w pomieszczeniu w ciągu np. tygodnia, posłużymy się pięcioma współrzędnymi
gdzie pierwsze trzy liczby to współrzędne punktu, a czwarta to temperatura. Chcąc opisać temperaturę w pomieszczeniu w ciągu np. tygodnia, posłużymy się pięcioma współrzędnymi 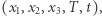 gdzie ostatnia wskazuje czas dokonywania pomiaru temperatury.
gdzie ostatnia wskazuje czas dokonywania pomiaru temperatury.
I choć opis takich wielowymiarowych przestrzeni nie sprawia żadnej trudności od strony formalnej, to nie można "zobaczyć" przestrzeni czterowymiarowej (i żadnej wyżej wymiarowej), gdyż nie mają one naturalnego odpowiednika.
Wróćmy na chwilę do niższych wymiarów - drugiego i trzeciego. Wspomniane na początku koło i kula są właściwie tym samym, tylko w różnych przestrzeniach: są to zbiory wszystkich punktów przestrzeni, których odległość od ustalonego środka jest nie większa od promienia 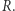 Takie pojęcie możemy przenieść na dowolny wymiar.
Takie pojęcie możemy przenieść na dowolny wymiar.
Definicja. Kulą 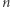 -wymiarową o środku w punkcie
-wymiarową o środku w punkcie 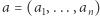 i promieniu
i promieniu 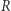 nazywamy zbiór
nazywamy zbiór

gdzie 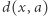 to odległość od
to odległość od 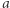 do
do  Z kulą wiążemy w sposób naturalny sferę, która jest zbiorem punktów odległych od danego punktu dokładnie o
Z kulą wiążemy w sposób naturalny sferę, która jest zbiorem punktów odległych od danego punktu dokładnie o 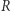

Zwróćmy uwagę na wskaźnik 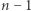 ; mimo iż sfera jest opisana w przestrzeni
; mimo iż sfera jest opisana w przestrzeni 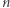 -wymiarowej, jest obiektem
-wymiarowej, jest obiektem 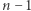 wymiarowym - jedna ze współrzędnych zawsze daje się wyrazić jako funkcja promienia i pozostałych
wymiarowym - jedna ze współrzędnych zawsze daje się wyrazić jako funkcja promienia i pozostałych 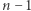 współrzędnych.
współrzędnych.
Można zastanowić się przez chwilę, ilu współrzędnych używamy do opisania położenia na Ziemi - oczywiście, wystarczą dwie: długość i szerokość geograficzna. I to mimo że powierzchnia naszej planety jest umieszczona w przestrzeni trójwymiarowej, więc naturalne jest myślenie o niej jak o obiekcie trójwymiarowym.
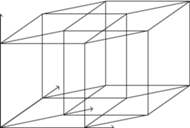
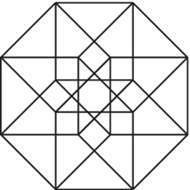
Tesserakt inaczej nazywany jest hipersześcianem. Na rysunku powyżej przedstawiony tak, aby zobrazować jego idealną symetrię.
Poniżej przedstawiamy jedną z wielu możliwości zdefiniowania kwadratu czy kostki w dowolnym wymiarze.
Definicja. Kostką  -wymiarową o boku długości 1 nazywamy zbiór
-wymiarową o boku długości 1 nazywamy zbiór

Powyższe opisuje kostkę, która ma wszystkie "ściany" równoległe do osi układu współrzędnych i której jeden z "rogów" znajduje się w jego środku. Chcąc opisać przesunięcie takiej kostki o ustalony wektor, trzeba by, oczywiście, lekko zmodyfikować wzór. Trochę trudniej jest opisać kostkę obróconą, ale tego na szczęście nie będziemy w dalszej części potrzebowali.
Oczywiście, 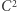 to klasyczny kwadrat, a
to klasyczny kwadrat, a 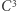 to sześcian. Kostkę
to sześcian. Kostkę 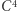 nazywamy tesseraktem - jest to czterowymiarowy odpowiednik sześcianu (więcej o nim w Małej Delcie).
nazywamy tesseraktem - jest to czterowymiarowy odpowiednik sześcianu (więcej o nim w Małej Delcie).
Zastanówmy się teraz, jak interpretować pole i objętość w dowolnym wymiarze. Posłużymy się w tym celu analogią do kostek, które dobrze znamy. Objętością obiektu jednowymiarowego jest jego długość. Dwuwymiarowego - pole, a trójwymiarowego - klasyczna objętość. Tym samym objętość kostki 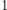 -wymiarowej o boku długości
-wymiarowej o boku długości 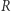 jest równa
jest równa 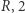 -wymiarowej to
-wymiarowej to 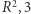 -wymiarowej to
-wymiarowej to 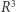 i przez analogię
i przez analogię 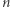 -wymiarowej
-wymiarowej 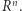
Powierzchni boczna 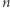 -wymiarowej bryły daje się przedstawić w przestrzeni o wymiar niższej niż sama bryła. W końcu siatkę
-wymiarowej bryły daje się przedstawić w przestrzeni o wymiar niższej niż sama bryła. W końcu siatkę 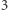 -wymiarowej kostki możemy przedstawić na płaszczyźnie, a "siatkę"
-wymiarowej kostki możemy przedstawić na płaszczyźnie, a "siatkę" 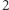 -wymiarowej kostki na prostej (będą to cztery odcinki). Ponownie przez analogię pole powierzchni bocznej
-wymiarowej kostki na prostej (będą to cztery odcinki). Ponownie przez analogię pole powierzchni bocznej  -wymiarowej bryły można interpretować jako objętość jej brzegu (
-wymiarowej bryły można interpretować jako objętość jej brzegu ( 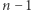 -wymiarowego).
-wymiarowego).
Przyjrzyjmy się teraz wielkości pola i objętości kostek i kul jednostkowych (o boku lub promieniu 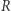 )
)

gdzie wzory dla kuli są zdefiniowane rekurencyjnie (wszystko przez analogię do kul jedno-, dwu- i trójwymiarowych),

Korzystając z powyższych wzorów, można podać wzory jawne dla pól i objętości kuli 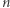 -wymiarowej. Poniżej podajemy te dla
-wymiarowej. Poniżej podajemy te dla 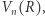 Czytelnikowi pozostawiając wyprowadzenie odpowiednich wzorów dla sfer
Czytelnikowi pozostawiając wyprowadzenie odpowiednich wzorów dla sfer

Anomalie
1. W kostkę 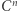 o boku długości
o boku długości 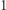 wpisujemy kulę
wpisujemy kulę 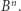 Jak będzie się zmieniał stosunek objętości kuli do kostki, gdy wymiar
Jak będzie się zmieniał stosunek objętości kuli do kostki, gdy wymiar 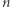 będzie rosnąć? Otóż odpowiednia proporcja dąży do… zera! Podobne zjawisko ma miejsce, gdy w kulę wpiszemy kostkę (patrz punkt 4). W obu przypadkach można to rozumieć w ten sposób, że wpisywane bryły coraz "gorzej" wypełniają to, w co są wpisywane.
będzie rosnąć? Otóż odpowiednia proporcja dąży do… zera! Podobne zjawisko ma miejsce, gdy w kulę wpiszemy kostkę (patrz punkt 4). W obu przypadkach można to rozumieć w ten sposób, że wpisywane bryły coraz "gorzej" wypełniają to, w co są wpisywane.

2. Obliczmy długość przekątnej 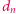
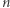 -wymiarowej kostki
-wymiarowej kostki 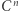 o boku długości
o boku długości 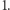 Znamy dobrze przypadek
Znamy dobrze przypadek 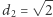 oraz
oraz 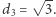 Nietrudno przekonać się, że
Nietrudno przekonać się, że 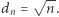 Tym samym przekątna kostki o boku 1 może przyjmować dowolnie dużą wartość (!) - tj. rośnie nieograniczenie wraz ze wzrostem wymiaru. Ponadto, promień kuli opisanej na tej kostce, równy połowie długości przekątnej, również rośnie bez ograniczenia. I wreszcie - maksymalna luka między powierzchnią kuli opisanej na kostce i tą kostką, wynosi
Tym samym przekątna kostki o boku 1 może przyjmować dowolnie dużą wartość (!) - tj. rośnie nieograniczenie wraz ze wzrostem wymiaru. Ponadto, promień kuli opisanej na tej kostce, równy połowie długości przekątnej, również rośnie bez ograniczenia. I wreszcie - maksymalna luka między powierzchnią kuli opisanej na kostce i tą kostką, wynosi 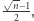 i również może przyjąć dowolnie dużą wartość. Tym samym można w lukę między kostką i powierzchnią kuli wpisać kulę o średnicy
i również może przyjąć dowolnie dużą wartość. Tym samym można w lukę między kostką i powierzchnią kuli wpisać kulę o średnicy 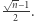 W wymiarze
W wymiarze 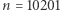 odpowiednia kula będzie miała średnicę 50 razy większą od długości boku kostki.
odpowiednia kula będzie miała średnicę 50 razy większą od długości boku kostki.
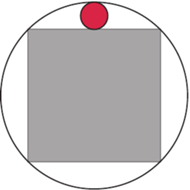
3. Punkty 1. oraz 2. wskazują, że wraz ze wzrostem wymiaru rośnie ilość przestrzeni między bryłami. Rozważmy tym razem sytuację analogiczną do przedstawionej na rysunku obok, tyle że 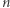 -wymiarową. Niech
-wymiarową. Niech  będzie szukanym promieniem małej kuli. Wtedy
będzie szukanym promieniem małej kuli. Wtedy

Granicą powyższego wyrażenia jest 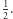 Oznacza to, że średnica opisanej przed chwilą kuli będzie coraz lepiej wypełniała przestrzeń w jednej z
Oznacza to, że średnica opisanej przed chwilą kuli będzie coraz lepiej wypełniała przestrzeń w jednej z 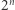 identycznych kostek, na jakie wyjściową kostkę daje się podzielić (średnica będzie coraz bliższa długości boku takiej kostki).
identycznych kostek, na jakie wyjściową kostkę daje się podzielić (średnica będzie coraz bliższa długości boku takiej kostki).
4. Coś prostszego: z punktu 2. wynika, że kostka jest coraz mniejsza w stosunku do kuli, w którą jest wpisana. Istotnie, jeżeli kula 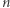 -wymiarowa o promieniu
-wymiarowa o promieniu 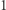 jest opisana na kostce, to bok takiej kostki ma długość
jest opisana na kostce, to bok takiej kostki ma długość 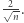 Tym samym objętość takiej kostki maleje wraz ze wzrostem wymiaru i może być dowolnie bliska zeru.
Tym samym objętość takiej kostki maleje wraz ze wzrostem wymiaru i może być dowolnie bliska zeru.

5. Jeśli w  -wymiarową kostkę o boku 1 wpiszemy
-wymiarową kostkę o boku 1 wpiszemy 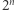 kul o średnicach
kul o średnicach 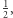 to kula styczna do wszystkich kul będzie miała promień równy
to kula styczna do wszystkich kul będzie miała promień równy 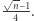 I tak, na przykład, w wymiarze
I tak, na przykład, w wymiarze 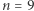 kula będzie jednocześnie kulą wpisaną w kostkę i styczną do
kula będzie jednocześnie kulą wpisaną w kostkę i styczną do 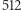 narożnych kul (!), a w wymiarach od
narożnych kul (!), a w wymiarach od 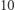 wzwyż taka kula będzie "wystawała" poza kostkę (wszystkie rogi kostki są zawsze na zewnątrz kuli)! Ponadto, jej promień może być dowolnie duży (wystarczy dobrać odpowiednie
wzwyż taka kula będzie "wystawała" poza kostkę (wszystkie rogi kostki są zawsze na zewnątrz kuli)! Ponadto, jej promień może być dowolnie duży (wystarczy dobrać odpowiednie  ), ale jest jednocześnie od góry ograniczona przez połowę długości przekątnej kostki
), ale jest jednocześnie od góry ograniczona przez połowę długości przekątnej kostki 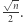 Tym samym powierzchnia takiej kuli nigdy nie "wyjdzie" całkowicie poza kostkę! A w takim razie to ta część "wystająca" poza kostkę ma objętość rosnącą do
Tym samym powierzchnia takiej kuli nigdy nie "wyjdzie" całkowicie poza kostkę! A w takim razie to ta część "wystająca" poza kostkę ma objętość rosnącą do 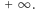 Czy ktoś potrafi to sobie wyobrazić?
Czy ktoś potrafi to sobie wyobrazić?
Anomalia dla bardziej zaawansowanych
6. Na koniec rzecz niezwykła. Gdy spojrzymy na pole koła i potraktujemy to wyrażenie jako funkcję zmiennej 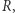 to
to

a więc pochodną pola koła jest obwód okręgu (długość brzegu koła). Podobne zjawisko ma miejsce dla objętości kuli i pola sfery (pola brzegu kuli)

Czy to przypadek, czy reguła? Otóż jest to zależność prawdziwa w dowolnym wymiarze! Liczby 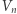 oraz
oraz 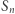 łączy następujący związek
łączy następujący związek

Nie jesteśmy w stanie wyobrazić sobie większości (lub wszystkich) z powyższych punktów. Intuicja wielowymiarowa całkowicie nas zawodzi i nie jest możliwe racjonalne przekonanie kogoś, że kula opisana w punkcie 5. może "wystawać" poza sześcian. Przeczy to całkowicie zdrowemu rozsądkowi, ale... Pamiętajmy, że w matematyce nie wszystko jest intuicyjne i zgodne z oczekiwaniami. Powyższe przykłady pokazują, jak ostrożnym należy być. Czytelników wiernych zasadzie "nie uwierzę, póki nie zobaczę" prosimy o wybaczenie. I o więcej ufności w rozumowania czysto analityczne.
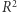 (klasyczne pole), lecz objętość brzegu tego kwadratu, a więc w tym przypadku długość czterech odcinków brzegowych (klasyczny obwód).
(klasyczne pole), lecz objętość brzegu tego kwadratu, a więc w tym przypadku długość czterech odcinków brzegowych (klasyczny obwód).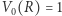 oraz
oraz 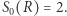 Pierwszy zbiór składa się z jednego punktu, drugi zaś z dwóch. Objętość w przestrzeni "zerowymiarowej" zlicza punkty należące do danego zbioru.
Pierwszy zbiór składa się z jednego punktu, drugi zaś z dwóch. Objętość w przestrzeni "zerowymiarowej" zlicza punkty należące do danego zbioru.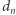 można obliczyć tak:
można obliczyć tak: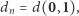
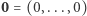 oraz
oraz 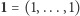 mają po
mają po 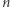 identycznych współrzędnych.
identycznych współrzędnych.