Drobiazgi
Małe Wszechświaty
Astrofizycy ostatnio twierdzą, że "Wszechświat jest płaski", co w ich żargonie oznacza, iż średnia krzywizna Wszechświata jest równa zeru (i tylko lokalnie jest zakłócana przez grawitację). Jeśli mają rację, to matematyka dowodzi, że Wszechświat przyjmuje jeden z 18 możliwych kształtów.
Wynika to z twierdzenia Felixa Kleina
Twierdzenie. Wszystkie lokalnie euklidesowe rozmaitości powstają z przestrzeni euklidesowej przez podzielenie jej przez jednostajnie nieciągłe podgrupy izometrii.
Wyjaśnijmy te terminy (rzecz jasna od końca).
Izometrie to przekształcenia zachowujące odległości. Grupa przekształceń to taki ich zbiór, w którym jest identyczność, wraz z każdym przekształceniem jest odwrotne do niego, a wraz z każdymi dwoma - ich złożenie. Podgrupa izometrii jest jednostajnie nieciągła, gdy każde z jej przekształceń odrzuca każdy niestały punkt co najmniej na z góry ustaloną odległość.
Podzielenie przez grupę polega na utożsamieniu (sklejeniu) tych wszystkich punktów, które dadzą się nałożyć przez któreś z przekształceń grupy.
Jeśli chcemy, by nasz model Wszechświata był ograniczony (czyli, by odległości w nim nie przekraczały jakiejś wielkości, np. 5 mld lat razy prędkość światła) i był orientowalny (patrz np. Co zobaczyła Alicja..., Delta 5/2017), to liczba możliwości maleje do sześciu. Te właśnie modele nazywa się Małymi Wszechświatami - chwilowo nie potrafimy stwierdzić, czy Wszechświat "wybrał" któryś z nich. Natomiast grupy astrofizyków wybierają dla siebie któryś z Małych Wszechświatów i piszą prace o tym, co by było, gdyby tak było; np. Wszechświat w łazience, Delta 1/2013.
Grupy określające te rozmaitości są wyznaczone, odpowiednio, przez przekształcenia
( 
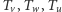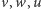nie leżą w jednej płaszczyźnie);
; 
;
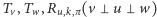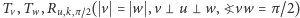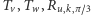(jak poprzednio, tylko 
);
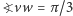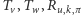(jak poprzednio, tylko 
);
( 
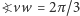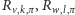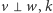i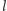 
skośne).
Ten pierwszy Mały Wszechświat powstaje z równoległościanu, w którym zlepiła się przednia ściana z tylną, lewa z prawą i górna z dolną. Wyobrażenie pozostałych pozostawiam Czytelnikom.