Jak krzywizna zżera przestrzeń
Cytat z General Relativity Johna Archibalda Wheelera, który został umieszczony u góry marginesu artykułu Michała Bejgera, można przejrzyście zilustrować geometrycznie, gdy zajmiemy się przestrzenią dwuwymiarową.
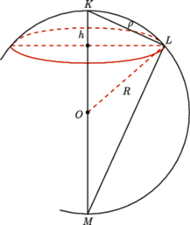
Rys. 1
Jak wiadomo, pole czaszy sferycznej to 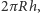 gdzie
gdzie 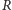 to promień sfery, a
to promień sfery, a 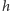 to wysokość czaszy. Skorzystanie ze "szkolnego" twierdzenia, że przyprostokątna w trójkącie prostokątnym jest średnią geometryczną przeciwprostokątnej i swojego rzutu na nią, pozwala na spostrzeżenie, że również na sferze pole koła dane jest wzorem
to wysokość czaszy. Skorzystanie ze "szkolnego" twierdzenia, że przyprostokątna w trójkącie prostokątnym jest średnią geometryczną przeciwprostokątnej i swojego rzutu na nią, pozwala na spostrzeżenie, że również na sferze pole koła dane jest wzorem 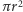 - trzeba tylko pamiętać, że owo
- trzeba tylko pamiętać, że owo  to przestrzenna odległość środka koła od brzegu, aby nie było nieporozumień, oznaczmy ją przez
to przestrzenna odległość środka koła od brzegu, aby nie było nieporozumień, oznaczmy ją przez 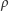 (Rys. 1). Faktycznie
(Rys. 1). Faktycznie 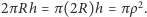
Dla mieszkańców sfery taki promień nie ma sensu. Dla nich promieniem koła na sferze jest łuk 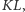 oznaczmy jego długość przez
oznaczmy jego długość przez 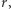 czyli jest to kąt
czyli jest to kąt 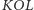 pomnożony przez
pomnożony przez 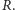 Ponieważ
Ponieważ 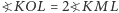 i
i 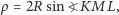 więc
więc

zatem pole koła na sferze to 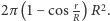
W szczególności pole koła o promieniu  na sferze jednostkowej to
na sferze jednostkowej to 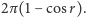
Rys. 2
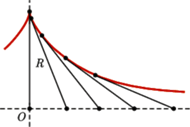
Rys. 3
Wracając do Wheelera, musimy rozważać nie tylko powierzchnie mające stałą krzywiznę dodatnią (jak sfera - jej krzywizna to 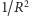 ), ale i te, które mają krzywiznę ujemną. Przyzwoitych "sfer" o stałej ujemnej krzywiźnie w przestrzeni trójwymiarowej nie ma. Ich najbliższą krewną jest pseudosfera (Rys. 2), powierzchnia powstała z obrotu traktrysy (Rys. 3). Długość wyznaczającego traktrysę odcinka (oznaczmy ją przez
), ale i te, które mają krzywiznę ujemną. Przyzwoitych "sfer" o stałej ujemnej krzywiźnie w przestrzeni trójwymiarowej nie ma. Ich najbliższą krewną jest pseudosfera (Rys. 2), powierzchnia powstała z obrotu traktrysy (Rys. 3). Długość wyznaczającego traktrysę odcinka (oznaczmy ją przez 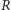 ) nazywamy promieniem pseudosfery. Jeśli pominąć jej "kant", to pseudosfera ma wszędzie krzywiznę równą
) nazywamy promieniem pseudosfery. Jeśli pominąć jej "kant", to pseudosfera ma wszędzie krzywiznę równą 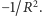
Rozumowanie analogiczne do przeprowadzonego dla sfery (choć już, niestety, bez "szkolnego" wsparcia) pozwala stwierdzić, że pole koła o promieniu  na pseudosferze jednostkowej to
na pseudosferze jednostkowej to 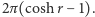
Zauważmy, że 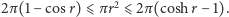 W tym celu należy tylko pamiętać,
W tym celu należy tylko pamiętać,

Mamy więc dla 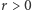

oraz

Zatem koła na powierzchni o krzywiźnie dodatniej mają mniejsze pole od kół o tym samym promieniu na płaszczyźnie, a koła na powierzchni o krzywiźnie ujemnej - pola większe. Można to interpretować tak, że krzywizna dodatnia zżera powierzchnię, przyciągając do siebie wszystko, a krzywizna ujemna rozpycha powierzchnię, wszystko od siebie odsuwając. Fizycy lubią te oddziaływania nazywać grawitacją.
I na koniec bardzo praktyczne spostrzeżenie krawieckie. Typowa spódnica, gdy jej "nosicielka" obraca się szybko w tańcu, przybiera kształt zbliżony do czaszy. Ale gdy jest uszyta z pełnego klosza, przy szybkich obrotach ułoży się płasko na poziomie talii. Gdy wreszcie wszyjemy w nią jeszcze więcej klinów (tak się często szyje spódnice dla zespołów folklorystycznych), przy obrotach będzie falowała, a jej brzeg będzie naśladował sinusoidę. Przykład, co to znaczy za mało - a co za dużo materiału, jest trafiony, ale chyba z tym przyciąganiem to - w przypadku spódnic - jest nie całkiem tak, jak chciałby Wheeler.