Mała Delta
Tam, gdzie matematyka, sztuka i magia łączą swoje siły, czyli słów kilka o origami

Mówi się, że origami powstało dwa tysiące lat temu wraz z wynalezieniem papieru. W tym kontekście wydaje się zaskakujące, że początek odkrywania matematyki stojącej za składaniem papieru przypada dopiero na lata osiemdziesiąte zeszłego stulecia. Dziś gałąź nauki zwana origami obliczeniowe (ang. computational origami) rozwija się bardzo prężnie.
Origamiści-teoretycy zadają sobie głównie dwa pytania: co da się złożyć ze z góry zadanego wzoru złożeń (tzw. foldability question) oraz jakie kształty można zaprojektować (tzw. design question). Bardzo często odpowiedzi udzielają - jeśli to tylko możliwe - komputery. Origami obliczeniowe w głównej mierze rozwija się dzięki algorytmom, z których niektóre zostały zaimplementowane w programach dostępnych bezpłatnie online.
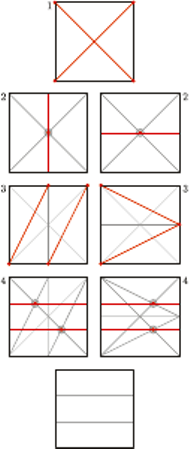
Podział kwadratu na trzy równe części. Istnieje wiele różnych sposobów ścisłego podzielenia kwadratowej kartki papieru na trzy identyczne prostokąty. Powyżej przedstawiamy dwa z nich
Niestety, rzadko mówi się o tym, że origami jest silniejsze niż konstrukcje przy użyciu cyrkla i linijki(!). Ale co to właściwie znaczy? Dwa sławne problemy starożytnej Grecji - trysekcja kąta i podwojenie objętości sześcianu - okazały się nierozwiązywalne za pomocą cyrkla i linijki. W czym tkwi istota sprawy? Oba zagadnienia sprowadzają się do rozwiązania równań stopnia trzeciego. Z kolei dzięki linijce i cyrklowi jesteśmy w stanie stworzyć tylko konstrukcje będące rozwiązaniami co najwyżej serii równań kwadratowych. I tu ukazuje nam się magia origami - dziecinnie proste składanie kartki papieru okazało się sposobem na rozwiązanie powyższych problemów, nad którymi głowili się starożytni. Poniżej przedstawiamy schematy trysekcji kąta i otrzymania odcinka długości 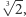 którego konstrukcja jest wystarczająca do rozwiązania problemu podwojenia sześcianu.
którego konstrukcja jest wystarczająca do rozwiązania problemu podwojenia sześcianu.
Konstrukcja odcinka długości 
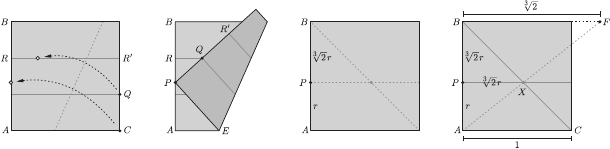
Chcąc podwoić sześcian o boku jeden, musimy po prostu skonstruować sześcian o krawędzi długości 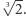 Wyznaczenie odcinka tej długości za pomocą składania papieru nie jest nadto skomplikowane. Wystarczy najpierw tak zgiąć kwadratową kartkę, aby powstałe dwa równoległe do boku zagięcia podzieliły go na trzy równe części (rysunek obok). Następnie (rysunek poniżej) zaginamy prawy dolny róg w ten sposób, aby punkt
Wyznaczenie odcinka tej długości za pomocą składania papieru nie jest nadto skomplikowane. Wystarczy najpierw tak zgiąć kwadratową kartkę, aby powstałe dwa równoległe do boku zagięcia podzieliły go na trzy równe części (rysunek obok). Następnie (rysunek poniżej) zaginamy prawy dolny róg w ten sposób, aby punkt  leżał na odcinku
leżał na odcinku 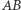 (oznaczmy to miejsce
(oznaczmy to miejsce 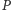 ) punkt
) punkt 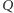 natomiast na odcinku
natomiast na odcinku 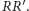 Okazuje się, że otrzymujemy następującą zależność:
Okazuje się, że otrzymujemy następującą zależność: 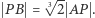 Dlaczego? Załóżmy, że odcinki
Dlaczego? Załóżmy, że odcinki 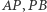 i
i 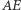 mają odpowiednio długości
mają odpowiednio długości 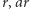 i
i 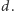 W tej sytuacji odcinki
W tej sytuacji odcinki 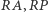 oraz
oraz 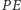 mierzą
mierzą 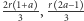 i
i 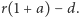 Stosując twierdzenie Pitagorasa do trójkąta
Stosując twierdzenie Pitagorasa do trójkąta 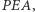 otrzymujemy, że
otrzymujemy, że 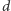 wynosi
wynosi 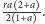 Ponieważ trójkąty
Ponieważ trójkąty 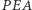 i
i 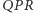 są podobne, dostajemy równość
są podobne, dostajemy równość 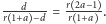 Po przekształceniach dochodzimy do interesującego nas wyniku
Po przekształceniach dochodzimy do interesującego nas wyniku 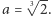 Korzystając z podobieństwa trójkątów
Korzystając z podobieństwa trójkątów 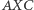 i
i 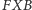 oraz trójkątów
oraz trójkątów 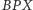 i
i 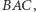 można łatwo wykazać, że odcinek
można łatwo wykazać, że odcinek  ma długość
ma długość 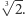
Trysekcja kąta
Kąt 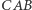 może zostać podzielony na trzy równe części w następujący sposób. Robimy zagięcia
może zostać podzielony na trzy równe części w następujący sposób. Robimy zagięcia 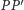 oraz
oraz 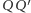 równoległe do podstawy
równoległe do podstawy 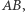 gdzie
gdzie 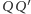 leży pośrodku pomiędzy pozostałymi dwoma (nie oznacza to jednak, że
leży pośrodku pomiędzy pozostałymi dwoma (nie oznacza to jednak, że 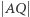 stanowi jedną trzecią boku kwadratu). Następnie wykonujemy takie złożenie, w wyniku którego punkt
stanowi jedną trzecią boku kwadratu). Następnie wykonujemy takie złożenie, w wyniku którego punkt 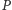 leży na odcinku
leży na odcinku 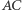 oraz punkt
oraz punkt 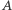 leży na odcinku
leży na odcinku 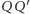 w pozycji
w pozycji 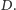 Kąt
Kąt 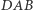 jest jedną trzecią wyjściowego kąta
jest jedną trzecią wyjściowego kąta 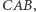 ponieważ trójkąty
ponieważ trójkąty 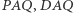 oraz
oraz 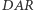 są przystające.
są przystające.
Co ciekawe, inaczej sformułowana aksjomatyka origami pozwala - w teorii - rozwiązać równania  -tego stopnia. Jest to jednak nieefektywne i niestosowane w praktyce.
-tego stopnia. Jest to jednak nieefektywne i niestosowane w praktyce.
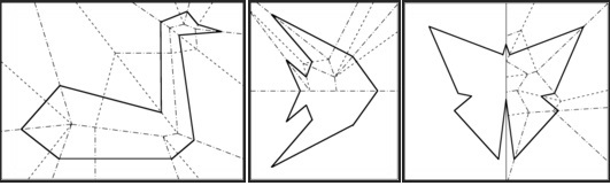
Jak wielu z nas zapewne słyszało, w klasycznym origami zabronione jest przecinanie papieru. Co się jednak stanie, jeśli dopuścimy cięcie? Jakie kształty jesteśmy w stanie otrzymać za pomocą złożenia papieru i - powiedzmy - jednego prostego cięcia? To tak zwany problem fold & one cut pochodzący z 1721 roku. Pojawił się on po raz pierwszy w japońskiej książce z zagadkami. Swego czasu zagadnienie to było nawet przedmiotem magicznych sztuczek. Problem został rozwiązany dopiero w 1998 roku przez Erika Demaine'a, Martina Demaine'a i Annę Lubiw. Udowodnili oni, że za pomocą jednego prostego przecięcia pojedynczej kartki papieru złożonej na płasko można otrzymać każdy kształt o prostych bokach. Możemy zatem wyciąć pojedynczy wielokąt, wiele rozłącznych wielokątów, zagnieżdżone wielokąty, przylegające wielokąty...
Spójrzmy na kilka przykładów. Wystarczy wykonać wyznaczone zagięcia i jedno proste cięcie wzdłuż powstałej linii, aby otrzymać łabędzia, rybę czy motyla.
Niektórzy mogą spytać, czy to już wszystko, co może nam zaoferować składanie papieru. Otóż nie! Techniki origami są również szeroko wykorzystywane w technologii i medycynie (m.in. przy składaniu teleskopów kosmicznych, paneli słonecznych, poduszek powietrznych, stentów). Warto wspomnieć, że w ostatnich latach niektórzy z origamistów pracują nad matematycznym modelem "zwijania białka" (ang. protein folding) - procesu fizycznego obecnego we wszystkich żywych organizmach i wirusach, co może mieć zastosowania w medycynie. Jak widzimy, origami to nie tylko rodzaj sztuki i rozrywki. To także potężne narzędzie matematyczne o szerokim wachlarzu zastosowań.