Co to jest?

Iloczyn skalarny

Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: 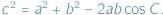$2 2 2 c = a + b − 2ab cosC:$ Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 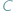$C$ jest prosty, czyli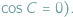 $cosC = 0):$

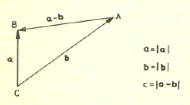
Dla bliższego zbadania geometrycznego i algebraicznego sensu twierdzenia kosinusów użyteczny jest zapis wektorowy, w którym boki trójkąta będą reprezentowane przez wektory 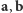$a,b$ i $a −b.$

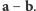
Oznacząjąc jak zwykle przez |aj długość wektora a otrzymamy wzór:

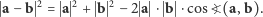
a− b 2 = a 2 + b 2− 2 a ⋅ b ⋅cos?(a, b).

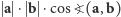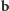Nazwijmy wyrażenie $a ⋅ b ⋅cos?(a, b)$ iloczynem skalarnym wektorów $|a$ i $b$ , oznaczmy je w skrócie symbolem 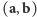$(a,b)$ i zbadajmy pewne szczególne własności tej funkcji.

Cały artykuł dostępny jest w wersji do druku [application/pdf]: (351 KB)