I.

Od dowolnego punktu do dowolnego innego można poprowadzić prostą.

II.

Ograniczoną prostą można dowolnie przedłużyć.

III.

Z dowolnego środka dowolnym promieniem można opisać okrąg.

IV.

Wszystkie kąty proste są równe.

V.

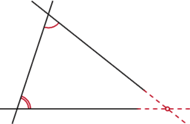
Jeśli dwie proste na płaszczyźnie tworzą z trzecią kąty jednostronne wewnętrzne o sumie mniejszej od dwóch kątów prostych (rysunek powyżej ), to proste te, po przedłużeniu, przetną się i to z tej właśnie strony.

Dzieło to było przez tysiąclecia uznawane za wzór ścisłości rozumowania dla wszystkich dyscyplin naukowych. Aż przyszły czasy, gdy matematycy tak dokładnie zaczęli przyglądać się swojej dyscyplinie i tak ostre kryteria narzucili rozumowaniom, że trzeba było uznać, iż postulaty Euklidesa można jedynie traktować jako wzorowy zapis intuicji tego, co być powinno. Ale tylko intuicji.

Jako pierwszy nowoczesną aksjomatykę geometrii euklidesowej, spełniającą wszelkie wymogi logiki matematycznej, podał w 1882 roku Moritz Pasch,

ale za naprawdę dobrą uznano dopiero aksjomatykę, którą zawarł David Hilbert w dziele Podstawy geometrii, którego tytuł stał się nazwą dyscypliny matematycznej badającej aksjomatyczne ujęcia geometrii.

Dobra to ta aksjomatyka była, ale, niestety, nie okazała się prosta i w żadnym razie nie nadawała się do tego, by np. uczyć według niej w szkole. Jej pojęciami pierwotnymi (czyli pojęciami, o których traktowały aksjomaty) były trzy rodzaje zmiennych (punkty, proste i płaszczyzny) oraz cztery relacje (leżenie na, leżenie między, przystawanie odcinków i przystawanie kątów). A aksjomatów było 20, z czego co najmniej jedna trzecia o stopniu komplikacji większym niż V postulat Euklidesa.

Powstało pytanie, czy dla geometrii euklidesowej istnieje aksjomatyka prosta i zrozumiała nie tylko dla profesjonalistów. Przede wszystkim zastanowiono się nad doborem pojęć pierwotnych.