Istnienie
Gdy chcemy coś badać, rozsądnie jest upewnić się, że to coś istnieje...
Euklides w III wieku p.n.e. pokazał, jak tworzyć matematyczną rzeczywistość na drodze aksjomatycznej. Istnieją, oczywiście, inne sposoby pomnażania matematycznych bytów i uzasadniania ich poprawności.
Problemy istnienia stanowią nieodłączną część matematyki i czasem wpływają
na jej rozwój. Wystarczy przypomnieć historię poszukiwania odpowiedzi na
pytania starożytnych Greków o istnienie konstrukcji platońskiej podwojenia
sześcianu, kwadratury koła, trysekcji kąta. W podstawach matematyki niezłego
zamieszania narobiły pytania o to, czy istnieje zbiór wszystkich zbiorów, czy
istnieje zbiór złożony ze wszystkich zbiorów, które nie są swoimi
elementami. Otwarte pytania w rodzaju – czy istnieje nieskończenie wiele
par liczb pierwszych postaci
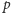 i
i
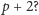 – nadal inspirują
matematyków.
– nadal inspirują
matematyków.
Na początku XX wieku rozliczne zastosowania równań (różniczkowych, całkowych) skupiły uwagę na następujących problemach:
- (1)
- Czy równanie ma rozwiązanie? Ile jest rozwiązań?
- (2)
- Gdzie rozwiązania są zlokalizowane? Jaka jest ich struktura?
- (3)
- Jak te rozwiązania wyznaczyć?
Odpowiedzią matematyków były dwa spektakularne twierdzenia o punktach
stałych (punkt stały przekształcenia
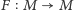 to taki punkt
to taki punkt
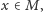 że
że
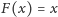 ). Sformułujemy je dla przestrzeni euklidesowych
). Sformułujemy je dla przestrzeni euklidesowych
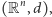 gdzie
gdzie
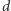 jest metryką. Należy podkreślić, że ten
rezultat nie przenosi się do przestrzeni o nieskończonym wymiarze.
jest metryką. Należy podkreślić, że ten
rezultat nie przenosi się do przestrzeni o nieskończonym wymiarze.
Twierdzenie 1 (Luitzen Brouwer, 1911 r.). Niech
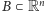 będzie domkniętą kulą jednostkową. Każde przekształcenie
ciągłe
będzie domkniętą kulą jednostkową. Każde przekształcenie
ciągłe
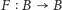 ma punkt stały.
ma punkt stały.

Rys. 1
Rys. 2
Twierdzenie 2 (Stefan Banach, 1922 r.). Przekształcenie
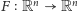 nazywamy
zwężającym, gdy istnieje taka stała
nazywamy
zwężającym, gdy istnieje taka stała
 że dla wszystkich
że dla wszystkich
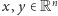 zachodzi
zachodzi
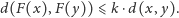 |
Każde przekształcenie zwężające
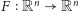 ma dokładnie jeden punkt
stały
ma dokładnie jeden punkt
stały
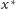 i granicą iteracji funkcji
i granicą iteracji funkcji
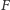 dla każdego
dla każdego
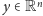 jest
właśnie ten punkt.
jest
właśnie ten punkt.
Sformułowania tych twierdzeń są optymalne. Antypodyczne
przekształcenie pierścienia
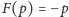 (Rys. 1), przekształcenie
koła bez brzegu
(Rys. 1), przekształcenie
koła bez brzegu
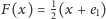 (Rys. 2), izometria
(Rys. 2), izometria
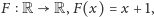 przekształcenie
przekształcenie
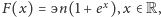 które
spełnia warunek
które
spełnia warunek
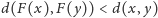 dla
dla
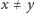 (ale nie istnieje
taka uniwersalna stała
(ale nie istnieje
taka uniwersalna stała
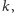 dla której byłby spełniony warunek
z twierdzenia Banacha), nie mają punktów stałych.
dla której byłby spełniony warunek
z twierdzenia Banacha), nie mają punktów stałych.
Działanie tych twierdzeń pokażemy na szkolnych zadaniach.
Rozważany ciąg zapisujemy rekurencyjnie:
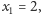
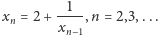
Z oszacowań
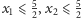 oraz z warunku
oraz z warunku
 |
wynika, że
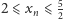 dla każdego
dla każdego
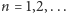
Ponieważ przekształcenie
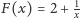 odwzorowuje przedział
odwzorowuje przedział
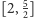 w siebie i jest zwężające,
w siebie i jest zwężające,
 |
więc na podstawie twierdzenia Banacha
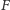 ma dokładnie jeden punkt stały
ma dokładnie jeden punkt stały
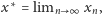 gdzie
gdzie
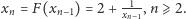 Rozwiązując
równanie
Rozwiązując
równanie
 otrzymujemy
otrzymujemy
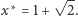
Uwaga. Każda liczba niewymierna ma dokładnie jedno rozwinięcie na
ułamek łańcuchowy arytmetyczny (wszystkie liczniki są równe
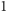 )
nieskończony:
)
nieskończony:
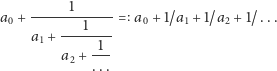 |
Leonhard Euler wykazał, że
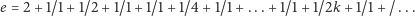 |
Dla liczby
 takie rozwinięcie nie jest znane! Wiadomo jedynie, jaka
jest wartość
takie rozwinięcie nie jest znane! Wiadomo jedynie, jaka
jest wartość
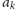 dla
dla
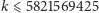 (Eric Weisstein, 2011
r.):
(Eric Weisstein, 2011
r.):
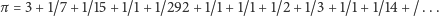 |
Od wiedzy, że „coś” istnieje, do wiedzy, jak to „coś” wygląda, droga czasem jest bardzo długa (jeśli w ogóle można ją przebyć).
Rys. 3
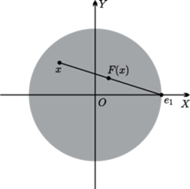
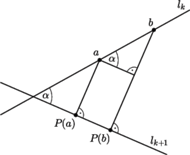
Zadanie 2. Na płaszczyźnie euklidesowej danych jest
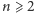 prostych
prostych
 Niech
Niech
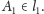 Rzut prostopadły
punktu
Rzut prostopadły
punktu
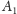 na prostą
na prostą
 wyznacza punkt
wyznacza punkt
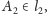 rzut
prostopadły
punktu
rzut
prostopadły
punktu
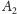 na prostą
na prostą
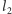 wyznacza punkt
wyznacza punkt
 itd.
Rzut prostopadły punktu
itd.
Rzut prostopadły punktu
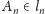 na prostą
na prostą
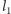 wyznacza punkt
wyznacza punkt
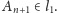 Czy istnieje taki punkt
Czy istnieje taki punkt
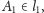 że
że
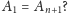
Jeśli proste
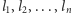 są równoległe, to każdy punkt
są równoległe, to każdy punkt
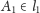 spełnia warunki zadania. Gdy istnieje para kolejnych prostych
spełnia warunki zadania. Gdy istnieje para kolejnych prostych
 i
i
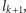 które nie są równoległe, to rzutowanie prostopadłe
które nie są równoległe, to rzutowanie prostopadłe
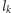 na
na
 jest przekształceniem zwężającym (Rys. 3)
jest przekształceniem zwężającym (Rys. 3)
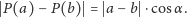 |
W tym przypadku przekształcenie
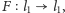 opisane w zadaniu, jest
zwężające ze stałą
opisane w zadaniu, jest
zwężające ze stałą
 gdzie
gdzie
 jest miarą jednego
z kątów między dwiema kolejnymi nierównoległymi prostymi. Zatem na
podstawie twierdzenia Banacha istnieje taki punkt
jest miarą jednego
z kątów między dwiema kolejnymi nierównoległymi prostymi. Zatem na
podstawie twierdzenia Banacha istnieje taki punkt
 że
że

Kolejne zadanie jest (chyba?) trudniejsze. Skoro łatwo wskazać przekształcenie
ciągłe koła z dziurą (pierścienia) na siebie bez punktu stałego, to dla koła
z większą liczbą dziur

Rys. 4
Zadanie 3. Niech
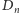 oznacza figurę domkniętą otrzymaną z koła,
w którym zrobiono
oznacza figurę domkniętą otrzymaną z koła,
w którym zrobiono
 dziur (Rys. 4). Wskazać przekształcenie
ciągłe zbioru
dziur (Rys. 4). Wskazać przekształcenie
ciągłe zbioru
 na siebie bez punktu stałego.
na siebie bez punktu stałego.
Rozwiązanie jest tutaj, ale najpierw spróbuj rozwiązać je sam.
Zastosowania twierdzeń Brouwera i Banacha w zaawansowanych działach matematyki, m.in. w teorii równań różniczkowych, całkowych, przyczyniły się do pojawienia się kolejnych wyników Juliusza Schaudera, Solomona Lefschetza, Karola Borsuka i wielu innych. Doprowadziło to do powstania użytecznej teorii punktów stałych, na którą dzisiaj można patrzeć z topologicznego lub metrycznego punktu widzenia.
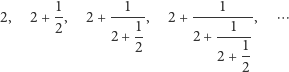
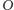 środek koła
środek koła
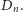 Jeżeli
Jeżeli
 to za
sprawą przekształcenia homeomorficznego możemy przyjąć, że dziury
są kołami tej samej wielkości, środek jednego z nich pokrywa się ze
środkiem koła
to za
sprawą przekształcenia homeomorficznego możemy przyjąć, że dziury
są kołami tej samej wielkości, środek jednego z nich pokrywa się ze
środkiem koła
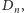 a środki pozostałych
a środki pozostałych
 kół
(
kół
(
 dziur) rozmieszczone są symetrycznie względem punktu
dziur) rozmieszczone są symetrycznie względem punktu
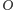 lub
są wierzchołkami
lub
są wierzchołkami
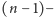 kąta foremnego (
kąta foremnego (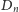 wokół punktu
wokół punktu
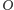 o kąt
o kąt
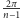 przekształca w sposób
ciągły figurę
przekształca w sposób
ciągły figurę
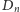 na siebie i przemieszcza każdy punkt figury
na siebie i przemieszcza każdy punkt figury
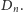

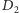 nadajemy
kształt sfery (
nadajemy
kształt sfery ( Złożenie symetrii względem płaszczyzny
Złożenie symetrii względem płaszczyzny
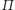 z obrotem sfery
o kąt
z obrotem sfery
o kąt
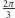 wokół osi
wokół osi
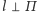 i przechodzącej przez środek
sfery przekształca figurę
i przechodzącej przez środek
sfery przekształca figurę
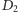 na siebie, przemieszczając jej każdy
punkt.
na siebie, przemieszczając jej każdy
punkt.
