Czy
 jest constans?
jest constans?
Jedną z najistotniejszych wielkości w matematyce jest
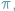 której
poświęcono wiele ścisłych prac i filozoficznych rozważań od starożytności
(jeszcze zanim została nazwana swoim obecnym imieniem) do czasów
współczesnych. Co pewien czas można znaleźć informacje o kolejnych
rekordach w wyznaczaniu coraz dłuższego jej rozwinięcia dziesiętnego.
Przeglądając literaturę, portale o tematyce matematycznej bądź podręczniki
szkolne, można także spotkać się z różnymi sposobami definiowania liczby
której
poświęcono wiele ścisłych prac i filozoficznych rozważań od starożytności
(jeszcze zanim została nazwana swoim obecnym imieniem) do czasów
współczesnych. Co pewien czas można znaleźć informacje o kolejnych
rekordach w wyznaczaniu coraz dłuższego jej rozwinięcia dziesiętnego.
Przeglądając literaturę, portale o tematyce matematycznej bądź podręczniki
szkolne, można także spotkać się z różnymi sposobami definiowania liczby
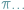

Według encyklopedii szkolnej „Matematyka”: liczba
 ludolfina,
stała matematyczna określona jako stosunek długości okręgu koła
do długości jego średnicy;
ludolfina,
stała matematyczna określona jako stosunek długości okręgu koła
do długości jego średnicy;
 Mając przed sobą
cytowaną definicję, spróbujmy zastanowić się, czy ów stosunek jest
ten sam dla każdego okręgu i odpowiadającej mu średnicy w ogólnym
przypadku.
Mając przed sobą
cytowaną definicję, spróbujmy zastanowić się, czy ów stosunek jest
ten sam dla każdego okręgu i odpowiadającej mu średnicy w ogólnym
przypadku.
Zaczniemy od geometrii sferycznej. Okręgiem na sferze nazywamy miejsce
geometryczne wszystkich jej punktów, których odległość od wybranego punktu
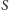 (na sferze) wynosi
(na sferze) wynosi
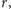 gdzie
gdzie
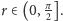 Odległości na
sferze można wyrażać w mierze kątowej lub łukowej. Nie powinno
więc budzić tu zdziwienia stwierdzenie, że, na przykład, długość
promienia okręgu wynosi
Odległości na
sferze można wyrażać w mierze kątowej lub łukowej. Nie powinno
więc budzić tu zdziwienia stwierdzenie, że, na przykład, długość
promienia okręgu wynosi
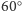 czy
czy
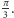 Dalej będziemy używać
miary łukowej. Punkt
Dalej będziemy używać
miary łukowej. Punkt
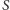 nazywamy środkiem (sferycznym), a
nazywamy środkiem (sferycznym), a
 – promieniem (sferycznym) okręgu. Okręgi sferyczne możemy
podzielić na małe i wielkie. Okręgi małe powstają wskutek przecięcia sfery
płaszczyzną nieprzechodzącą przez jej środek
– promieniem (sferycznym) okręgu. Okręgi sferyczne możemy
podzielić na małe i wielkie. Okręgi małe powstają wskutek przecięcia sfery
płaszczyzną nieprzechodzącą przez jej środek
 Okręgi wielkie to
zbiory punktów przecięcia sfery z pewną płaszczyzną przechodzącą przez
jej środek.
Okręgi wielkie to
zbiory punktów przecięcia sfery z pewną płaszczyzną przechodzącą przez
jej środek.
Taki okrąg, na przykład równik kuli ziemskiej, ma promień
 i dwa
środki będące punktami antypodycznymi (na Ziemi są to bieguny).
Najkrótszym połączeniem, czyli linią geodezyjną lub ortodromą, dwóch
punktów sfery jest właśnie krótszy łuk przechodzącego przez nie okręgu
wielkiego. Jeśli te łuki są równej długości, to oba są najkrótszymi
połączeniami. Okrąg wielki jest więc odpowiednikiem prostej euklidesowej. Ta
sferyczna prosta ma skończoną długość i jest zamknięta.
i dwa
środki będące punktami antypodycznymi (na Ziemi są to bieguny).
Najkrótszym połączeniem, czyli linią geodezyjną lub ortodromą, dwóch
punktów sfery jest właśnie krótszy łuk przechodzącego przez nie okręgu
wielkiego. Jeśli te łuki są równej długości, to oba są najkrótszymi
połączeniami. Okrąg wielki jest więc odpowiednikiem prostej euklidesowej. Ta
sferyczna prosta ma skończoną długość i jest zamknięta.
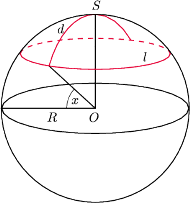
Rys. 1 Okrąg sferyczny i jego średnica. To, że ograniczone przez ten okrąg koło ma mniejsze pole niż płaskie koło o tym samym promieniu, wyraża fakt, iż to pole jest takie, jak pole płaskiego koła o promieniu będącym przestrzenną (!) odległością jego środka od brzegu.
Ustalmy promień sfery
 Długość równika wynosi
Długość równika wynosi
 a długość jego średnicy
a długość jego średnicy
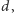 równa dwóm długościom
sferycznego promienia równika, jest połową długości równika, czyli
równa dwóm długościom
sferycznego promienia równika, jest połową długości równika, czyli
 Zatem stosunek długości okręgu wielkiego do długości
jego średnicy w tej sytuacji jest równy 2. Długość i średnicę
okręgu równoleżnikowego, leżącego na szerokości geograficznej
Zatem stosunek długości okręgu wielkiego do długości
jego średnicy w tej sytuacji jest równy 2. Długość i średnicę
okręgu równoleżnikowego, leżącego na szerokości geograficznej
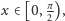 można wyrazić za pomocą wzorów
można wyrazić za pomocą wzorów

A każdy okrąg na sferze można przedstawić jako okrąg równoleżnikowy – trzeba zmienić położenie równika tak, żeby jego płaszczyzna była równoległa do płaszczyzny wyznaczonej przez wybrany okrąg. Względem nowego równika możemy obliczyć szerokość geograficzną wybranego okręgu.
Na przykład, dla szerokości geograficznej równej
 długość
odpowiadającego jej okręgu małego równa jest połowie długości równika,
czyli
długość
odpowiadającego jej okręgu małego równa jest połowie długości równika,
czyli
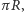 a średnica ma długość
a średnica ma długość
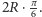 Zatem w tym
przypadku stosunek długości okręgu i jego średnicy jest równy 3.
Zatem w tym
przypadku stosunek długości okręgu i jego średnicy jest równy 3.
Zobaczyliśmy kilka przykładów, a teraz warto zadać ogólne pytanie
o zakres wartości stosunku długości dowolnego okręgu do jego średnicy na
sferze. Żeby łatwiej opisać dalsze obliczenia, wprowadźmy funkcję
 wyrażającą stosunek długości okręgu do długości odpowiadającej
mu średnicy. Ponieważ wszystkie okręgi na danej szerokości geograficznej są
takie same, parametrem funkcji będzie właśnie szerokość geograficzna.
Ogólny wzór, dla
wyrażającą stosunek długości okręgu do długości odpowiadającej
mu średnicy. Ponieważ wszystkie okręgi na danej szerokości geograficznej są
takie same, parametrem funkcji będzie właśnie szerokość geograficzna.
Ogólny wzór, dla
 to
to

a po podstawieniu otrzymujemy

Funkcja
 jest więc rosnąca w rozpatrywanej dziedzinie, a zbiór jej
wartości to odcinek
jest więc rosnąca w rozpatrywanej dziedzinie, a zbiór jej
wartości to odcinek
 Stosunek długości okręgu do długości jego
średnicy na sferze nie tylko nie jest wielkością stałą, ale opisuje go całkiem
nietrywialna funkcja.
Stosunek długości okręgu do długości jego
średnicy na sferze nie tylko nie jest wielkością stałą, ale opisuje go całkiem
nietrywialna funkcja.
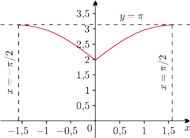
Rys. 2 Wykres funkcji
 dla okręgów sferycznych.
dla okręgów sferycznych.
Dziedzinę funkcji
 zawęziliśmy dotąd do przedziału
zawęziliśmy dotąd do przedziału
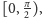 co
odpowiada półsferze bez bieguna o dodatniej (północnej) szerokości
geograficznej. Jednak w obliczeniach uwzględniliśmy wszystkie możliwe
długości okręgów na sferze, czyli właściwie znamy już wartości funkcji
co
odpowiada półsferze bez bieguna o dodatniej (północnej) szerokości
geograficznej. Jednak w obliczeniach uwzględniliśmy wszystkie możliwe
długości okręgów na sferze, czyli właściwie znamy już wartości funkcji
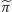 na przedziale
na przedziale
 Następujący wzór jest uogólnieniem
poprzedniego na ujemne szerokości geograficzne:
Następujący wzór jest uogólnieniem
poprzedniego na ujemne szerokości geograficzne:

Wykres parzystej funkcji
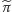 dla
dla
 przedstawia rysunek
2 .
przedstawia rysunek
2 .
W granicznym przypadku, gdy promień sferyczny
 małego okręgu
dąży do zera, okrąg sferyczny coraz bardziej „rozpłaszcza się” – wówczas
małego okręgu
dąży do zera, okrąg sferyczny coraz bardziej „rozpłaszcza się” – wówczas
 jest bliskie
jest bliskie
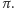 Jako model Ziemi najczęściej przyjmuje się
sferę lub elipsoidę obrotową, których powierzchnię lokalnie aproksymuje się
płaszczyzną euklidesową styczną w danym punkcie. Dla wielu zastosowań jest to
zabieg dopuszczalny, ponieważ wystarcza do otrzymania wymaganej
dokładności wyników. Ale nie zawsze – w geodezji, nawigacji, kartografii czy
astronomii znamy wiele przykładów, gdzie przybliżenie płaszczyzną
nie wystarcza, a na obserwowanym obszarze wartość funkcji
Jako model Ziemi najczęściej przyjmuje się
sferę lub elipsoidę obrotową, których powierzchnię lokalnie aproksymuje się
płaszczyzną euklidesową styczną w danym punkcie. Dla wielu zastosowań jest to
zabieg dopuszczalny, ponieważ wystarcza do otrzymania wymaganej
dokładności wyników. Ale nie zawsze – w geodezji, nawigacji, kartografii czy
astronomii znamy wiele przykładów, gdzie przybliżenie płaszczyzną
nie wystarcza, a na obserwowanym obszarze wartość funkcji
 istotnie
różni się od
istotnie
różni się od
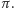 W takich przypadkach granice aproksymacyjnego
stosowania płaskiej geometrii euklidesowej należy wyraźnie określić.
W takich przypadkach granice aproksymacyjnego
stosowania płaskiej geometrii euklidesowej należy wyraźnie określić.
Na przykład, w pomiarach terenowych – wykorzystywanych lokalnie w geodezji
niższej – obszar powierzchni Ziemi można traktować jako płaski wtedy, gdy
znajduje się on w kole o promieniu około 15,5 km (wówczas jego powierzchnia
nie przekracza 760 km
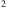 ). Odpowiada to w przybliżeniu polu koła
o średnicy równej
). Odpowiada to w przybliżeniu polu koła
o średnicy równej
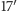 łuku okręgu wielkiego. Wyniki bezpośrednich
pomiarów, nieuwzględniających wpływu krzywizny powierzchni Ziemi,
wykonanych w takim obszarze, można przedstawić na płaszczyźnie
w odpowiedniej skali, pomijając odwzorowanie kartograficzne, i efekt będzie
satysfakcjonujący.
łuku okręgu wielkiego. Wyniki bezpośrednich
pomiarów, nieuwzględniających wpływu krzywizny powierzchni Ziemi,
wykonanych w takim obszarze, można przedstawić na płaszczyźnie
w odpowiedniej skali, pomijając odwzorowanie kartograficzne, i efekt będzie
satysfakcjonujący.
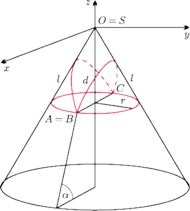
Rys. 3 Okrąg równoleżnikowy na stożku obrotowym i jego średnice.
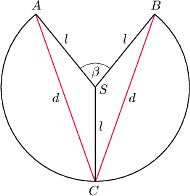
Rys. 4 Powierzchnia boczna stożka po rozwinięciu na płaszczyźnie. Kolorem zaznaczone są średnice narysowanego okręgu.
Zobaczmy teraz, jak zachowują się okręgi na stożku obrotowym. Stożek
obrotowy to powierzchnia powstała przez obrót prostej
 (
(
 ) nachylonej do osi
) nachylonej do osi
 pod kątem
pod kątem
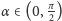 dokoła osi
dokoła osi
 w prostokątnym układzie współrzędnych
w prostokątnym układzie współrzędnych
 Przyjmijmy,
że
Przyjmijmy,
że
 czyli patrzmy tylko na jedną część stożka, tę pod
płaszczyzną
czyli patrzmy tylko na jedną część stożka, tę pod
płaszczyzną
 (Rys. 3). Spróbujmy powiedzieć coś o zbiorze
wartości funkcji
(Rys. 3). Spróbujmy powiedzieć coś o zbiorze
wartości funkcji
 określonej, jak poprzednio, jako stosunek długości
okręgu do długości jego średnicy.
określonej, jak poprzednio, jako stosunek długości
okręgu do długości jego średnicy.
Rozważmy rodzinę okręgów leżących na stożku, które powstają
w wyniku przecięcia go płaszczyznami równoległymi do płaszczyzny
 Okręgi te nazywamy, analogicznie jak na sferze, równoleżnikami.
Punkt
Okręgi te nazywamy, analogicznie jak na sferze, równoleżnikami.
Punkt
 wierzchołek stożka, jest zarazem środkiem wszystkich
okręgów równoleżnikowych. Intuicyjnie stwierdzamy, że powierzchnię
boczną stożka obrotowego można otrzymać, zwijając kawałek papieru, czego
z powierzchnią sfery zrobić się nie da. Spróbujmy więc spojrzeć na nasz
problem, rozkładając powierzchnię boczną stożka na płaszczyźnie.
Po tej operacji otrzymamy koło bez wycinka o kącie o mierze łukowej
wierzchołek stożka, jest zarazem środkiem wszystkich
okręgów równoleżnikowych. Intuicyjnie stwierdzamy, że powierzchnię
boczną stożka obrotowego można otrzymać, zwijając kawałek papieru, czego
z powierzchnią sfery zrobić się nie da. Spróbujmy więc spojrzeć na nasz
problem, rozkładając powierzchnię boczną stożka na płaszczyźnie.
Po tej operacji otrzymamy koło bez wycinka o kącie o mierze łukowej
 przedstawione na rysunku 4 . Na tym samym rysunku widać
okrąg na stożku, którego długość obliczymy. Niech
przedstawione na rysunku 4 . Na tym samym rysunku widać
okrąg na stożku, którego długość obliczymy. Niech
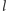 oznacza
długość odcinka
oznacza
długość odcinka
 Nasze obliczenia będą zależały od dwóch
parametrów – odległości
Nasze obliczenia będą zależały od dwóch
parametrów – odległości
 okręgu od wierzchołka stożka oraz kąta
okręgu od wierzchołka stożka oraz kąta
 charakteryzującego stożek.
charakteryzującego stożek.
Długość pełnego okręgu na płaszczyźnie to
 Od niej trzeba odjąć
długość łuku poza rozłożoną powierzchnią stożka, czyli
Od niej trzeba odjąć
długość łuku poza rozłożoną powierzchnią stożka, czyli
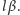 Wobec
tego długość równoleżnika leżącego w odległości
Wobec
tego długość równoleżnika leżącego w odległości
 od
wierzchołka
od
wierzchołka
 jest równa
jest równa

Trudniejsza sprawa jest ze średnicami. Mogłoby się wydawać, że
średnica takiego okręgu równoleżnikowego przechodzi przez punkt
 – otóż nie! Na rysunku 4 widać, jak wyglądają najkrótsze odcinki
(
– otóż nie! Na rysunku 4 widać, jak wyglądają najkrótsze odcinki
(
 i
i
 ) łączące przeciwległe punkty równoleżnika. Ich
długość
) łączące przeciwległe punkty równoleżnika. Ich
długość
 wyznaczymy, korzystając z twierdzenia cosinusów dla
trójkąta
wyznaczymy, korzystając z twierdzenia cosinusów dla
trójkąta
 :
:

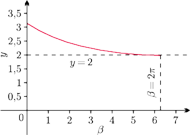
Rys. 5 Wykres funkcji
 dla okręgów równoleżnikowych stożka obrotowego.
dla okręgów równoleżnikowych stożka obrotowego.
Teraz możemy obliczyć
 :
:

Okazuje się, że wartość funkcji
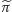 nie zależy od
nie zależy od
 czyli na
każdym stożku wszystkie równoleżniki mają ten sam stosunek długości
okręgu do średnicy. Ale ta liczba jest różna dla różnych stożków –
zależy od kąta
czyli na
każdym stożku wszystkie równoleżniki mają ten sam stosunek długości
okręgu do średnicy. Ale ta liczba jest różna dla różnych stożków –
zależy od kąta
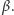 Funkcja, którą możemy zapisywać teraz
jako
Funkcja, którą możemy zapisywać teraz
jako
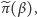 przyjmuje wartości z przedziału
przyjmuje wartości z przedziału
 dla
dla
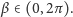
Czytelnik Wnikliwy z pewnością zapyta, co się zmieni, jeśli uwzględnimy też
okręgi, które nie są równoleżnikami. Czy nadal stosunek długości okręgu do
średnicy będzie stały na każdym stożku? Można zacząć od takiego zadania:
na powierzchni bocznej stożka obrotowego o ustalonym kącie
 dany
jest okrąg o promieniu
dany
jest okrąg o promieniu
 i środku
i środku
 niebędącym
wierzchołkiem stożka. Czy okrąg równoleżnikowy o takim samym
promieniu ma taką samą długość? Lub ogólniej, czy jest prawdą, że na
powierzchni bocznej stożka obrotowego dla dowolnej liczby
niebędącym
wierzchołkiem stożka. Czy okrąg równoleżnikowy o takim samym
promieniu ma taką samą długość? Lub ogólniej, czy jest prawdą, że na
powierzchni bocznej stożka obrotowego dla dowolnej liczby
 istnieje
nieskończenie wiele okręgów o promieniu
istnieje
nieskończenie wiele okręgów o promieniu
 ale różnej długości?
ale różnej długości?
Obliczyliśmy, że funkcja
 nie jest stała w ogólnym przypadku.
Wobec tego nieostrożnie byłoby stwierdzić bez zastanowienia, że liczba
nie jest stała w ogólnym przypadku.
Wobec tego nieostrożnie byłoby stwierdzić bez zastanowienia, że liczba
 wyraża wartość stosunku długości okręgu do długości jego
średnicy. Tak jest istotnie w geometrii euklidesowej na płaszczyźnie, do czego
przyzwyczaja się nas niemal od początków nauki w szkole. Ale, jak widać,
przenoszenie przyzwyczajeń z jednej, „ulubionej” geometrii na inne nie zawsze
jest dobrym pomysłem.
wyraża wartość stosunku długości okręgu do długości jego
średnicy. Tak jest istotnie w geometrii euklidesowej na płaszczyźnie, do czego
przyzwyczaja się nas niemal od początków nauki w szkole. Ale, jak widać,
przenoszenie przyzwyczajeń z jednej, „ulubionej” geometrii na inne nie zawsze
jest dobrym pomysłem.
W przykładach otrzymaliśmy wyłącznie wartości funkcji
 nieprzekraczające
nieprzekraczające
 Czy może się zdarzyć, że
Czy może się zdarzyć, że
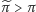 ? Odpowiedzi proszę
spróbować poszukać w geometrii hiperbolicznej.
? Odpowiedzi proszę
spróbować poszukać w geometrii hiperbolicznej.
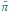 dla okręgów sferycznych.
dla okręgów sferycznych.
 dla okręgów równoleżnikowych stożka obrotowego.
dla okręgów równoleżnikowych stożka obrotowego.