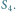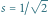Fraktalny świat papierowej tasiemki

Weźmy długi pasek papieru i złóżmy go na pół. Następnie, nie rozkładając,
złóżmy go w tę samą stronę jeszcze dwa razy. W końcu, rozprostujmy
złożenia tak, by papier zginał się pod kątem
 Otrzymamy obiekt jak
na rysunku 1.
Otrzymamy obiekt jak
na rysunku 1.

Rys. 1 Składanie paska papieru.
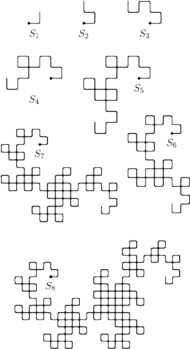
Rys. 2 Rodzina smoczych krzywych.
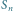 jest krzywa rzędu
jest krzywa rzędu
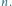
Jeśli przerysujemy kształt, który przyjmuje górna krawędź tasiemki,
dostaniemy ciekawą krzywą. Gdy złożymy papier nie trzy, ale cztery lub
więcej razy, krzywa, jaką otrzymamy, stanie się bardziej złożona (Rys. 2).
Coraz bardziej przypominać będzie brodzącego w wodzie smoka, stąd
też jej nazwa – smocza krzywa. Po raz pierwszy była badana w roku
1966 przez fizyków z NASA: Johna Heighwaya i Williama Hartera.
Do jej popularyzacji przyczynili się Martin Gardner w swoich Grach
Matematycznych oraz pisarz Michael Crichton: jeden z bohaterów jego
powieści Park Jurajski, specjalizujący się w teorii chaosu matematyk
Ian Malcolm, ilustrował za pomocą smoczej krzywej swoje przemyślenia
na temat przyszłości tak skomplikowanych przedsięwzięć, jak wskrzeszanie
wymarłych gadów. Swoją drogą, krzywa
 równie dobrze jak smoka
przypomina dinozaura.
równie dobrze jak smoka
przypomina dinozaura.
Jeśli całkowicie rozprostujemy tasiemkę, to na jej powierzchni dostrzeżemy
rowki i górki. Odpowiadają one zakrętom, które będziemy brać, jeśli
poczynając od wyróżnionego końca krzywej, będziemy ją rysować
ołówkiem: rowek to zakręt w lewo (
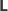 ), górka – w prawo (
), górka – w prawo (
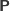 ).
Jeśli zgięliśmy papier
).
Jeśli zgięliśmy papier
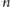 razy, wskutek czego otrzymaliśmy krzywą
rzędu
razy, wskutek czego otrzymaliśmy krzywą
rzędu
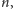 to zrobimy
to zrobimy
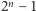 zakrętów. Oznaczmy przez
zakrętów. Oznaczmy przez
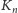 słowo składające się z liter
słowo składające się z liter
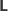 i
i
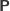 , opisujące ciąg
zakrętów na krzywej rzędu
, opisujące ciąg
zakrętów na krzywej rzędu
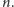 Mamy:
Mamy:

Ponieważ nasze możliwości składania papieru są dość ograniczone,
spróbujmy znaleźć jakąś regułę opisującą słowo
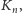 która pozwoli
nam rysować dowolnie duże krzywe bez konieczności proszenia o pomoc
specjalisty od origami. Złóżmy tasiemkę
która pozwoli
nam rysować dowolnie duże krzywe bez konieczności proszenia o pomoc
specjalisty od origami. Złóżmy tasiemkę
 razy, a następnie rozprostujmy
ostatnie
razy, a następnie rozprostujmy
ostatnie
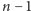 złożeń. Na powierzchni widzimy
złożeń. Na powierzchni widzimy
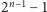 zagięć,
które powstały ze złożenia paska
zagięć,
które powstały ze złożenia paska
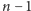 razy, zatem opisuje je słowo
razy, zatem opisuje je słowo
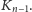 Jeśli rozprostujemy pasek papieru
Jeśli rozprostujemy pasek papieru
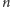 -ty raz, to będą one
pierwszymi zagięciami, zatem słowo
-ty raz, to będą one
pierwszymi zagięciami, zatem słowo
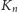 zawsze zaczyna się od
zawsze zaczyna się od
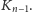 Zauważmy ponadto, że rowki na jednej połówce papieru
odpowiadają górkom na drugiej połówce i vice versa. Innymi słowy, jeśli
Zauważmy ponadto, że rowki na jednej połówce papieru
odpowiadają górkom na drugiej połówce i vice versa. Innymi słowy, jeśli
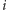 -tym zagięciem (dla
-tym zagięciem (dla
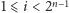 ) w
) w
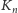 jest rowek, to
jest rowek, to
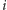 -tym zagięciem od końca będzie górka. Wprowadźmy operację
-tym zagięciem od końca będzie górka. Wprowadźmy operację
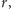 która odwraca kolejność liter w słowie i jednocześnie zamienia
litery
która odwraca kolejność liter w słowie i jednocześnie zamienia
litery
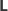 z
z
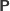 , dla przykładu
, dla przykładu
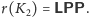 Wtedy
Wtedy

Sprawdzamy, że istotnie
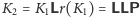 oraz
oraz
 Tym sposobem uzyskaliśmy rekurencyjny wzór na
słowo
Tym sposobem uzyskaliśmy rekurencyjny wzór na
słowo
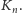 Okazuje się jednak, że może być ono opisane również
w inny sposób. Złóżmy pasek papieru
Okazuje się jednak, że może być ono opisane również
w inny sposób. Złóżmy pasek papieru
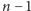 razy, rozprostujmy go,
a następnie pomalujmy zagięcia. Następnie złóżmy go znowu, tym razem
razy, rozprostujmy go,
a następnie pomalujmy zagięcia. Następnie złóżmy go znowu, tym razem
 razy, i rozprostujmy. Zauważmy, że
razy, i rozprostujmy. Zauważmy, że
 -te złożenie
spowodowało powstanie
-te złożenie
spowodowało powstanie
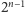 nowych zagięć, które pojawiły się
pomiędzy pomalowanymi zagięciami. Co więcej, nowe zagięcia występują
regularnie: na przemian rowek i górka. To pozwala nam wyprowadzić nowy
wzór: aby uzyskać
nowych zagięć, które pojawiły się
pomiędzy pomalowanymi zagięciami. Co więcej, nowe zagięcia występują
regularnie: na przemian rowek i górka. To pozwala nam wyprowadzić nowy
wzór: aby uzyskać
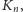 wstawiamy puste pola na początku i na końcu
słowa
wstawiamy puste pola na początku i na końcu
słowa
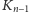 oraz między jego kolejnymi literami. Następnie wpisujemy
w puste pola na przemian litery
oraz między jego kolejnymi literami. Następnie wpisujemy
w puste pola na przemian litery
 i
i
 Zatem
Zatem
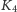 powstaje
następująco:
powstaje
następująco:

Powyższa metoda jest również rekurencyjna (tzn. odwołuje się do słów dla
mniejszych krzywych), ponadto obie metody konstruują słowa w całości. A co,
gdybyśmy chcieli mieć wzór na
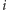 -ty zakręt na krzywej rzędu
-ty zakręt na krzywej rzędu
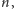 tzn. na
tzn. na
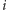 -tą (
-tą (
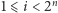 ) literę słowa
) literę słowa
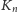 ? To proste:
z tego, co powiedzieliśmy, wynika, że jeśli
? To proste:
z tego, co powiedzieliśmy, wynika, że jeśli
 jest nieparzyste,
to tą literą jest
jest nieparzyste,
to tą literą jest
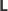 lub
lub
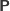 w zależności od parzystości
w zależności od parzystości
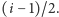 W przeciwnym przypadku jest to litera
W przeciwnym przypadku jest to litera
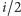 w słowie
w słowie
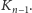 Tak więc jeśli
Tak więc jeśli
 jest największą potęgą dwójki dzielącą
jest największą potęgą dwójki dzielącą
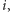 czyli
czyli
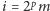 dla nieparzystego
dla nieparzystego
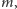 to szukaną literą jest
to szukaną literą jest
 wtedy, gdy
wtedy, gdy
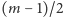 jest parzyste.
jest parzyste.
Ponieważ słowo
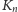 zawsze zaczyna się od
zawsze zaczyna się od
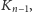 więc krzywą
rzędu
więc krzywą
rzędu
 możemy narysować, przedłużając krzywą rzędu
możemy narysować, przedłużając krzywą rzędu
 Z tego wynika naturalna konstrukcja nieskończonej smoczej
krzywej, która odpowiada słowu
Z tego wynika naturalna konstrukcja nieskończonej smoczej
krzywej, która odpowiada słowu


Rys. 3 Proces budowania krzywej
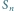 (linia ciągła) na krzywej
(linia ciągła) na krzywej
 (linia
przerywana).
(linia
przerywana).
Rysując smoczą krzywą coraz wyższych rzędów, dostrzeżemy jej zaskakującą
własność: krzywa ta nie ma samoprzecięć! Co więcej, o ile będziemy
pamiętali, by na każdym zakręcie robić mały łuk, to krzywa ta żadnego
punktu nie odwiedza dwa razy. Zanim udowodnimy, że jest tak w istocie,
spójrzmy na jeszcze jeden sposób, w jaki możemy otrzymać smoczą
krzywą. Zacznijmy od odcinka o długości 1, który jest smoczą krzywą
rzędu 0; oznaczmy go przez
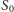 (Rys. 3). Teraz zbudujmy na tym odcinku
trójkąt prostokątny równoramienny, dorysowując dwa odcinki o długościach
(Rys. 3). Teraz zbudujmy na tym odcinku
trójkąt prostokątny równoramienny, dorysowując dwa odcinki o długościach
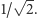 Te przyprostokątne tworzą krzywą rzędu 1. I dalej: na krzywej
Te przyprostokątne tworzą krzywą rzędu 1. I dalej: na krzywej
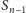 dobudowujemy
dobudowujemy
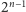 trójkątów, naprzemiennie po prawej
i lewej stronie krzywej – w ten sposób uzyskujemy
trójkątów, naprzemiennie po prawej
i lewej stronie krzywej – w ten sposób uzyskujemy
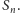 Zauważmy, że
choć krzywa
Zauważmy, że
choć krzywa
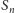 składa się z
składa się z
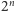 kawałków, to jej długość
wynosi
kawałków, to jej długość
wynosi
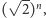 gdyż odcinki kolejnych rzędów są
gdyż odcinki kolejnych rzędów są
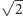 razy
krótsze. Jeśli będziemy wykonywać tę operację dalej, to w granicy otrzymamy
nieskończonej długości fraktalną krzywą zwaną smokiem Heighwaya. Smoczą
krzywą możemy więc traktować jako aproksymację smoka.
razy
krótsze. Jeśli będziemy wykonywać tę operację dalej, to w granicy otrzymamy
nieskończonej długości fraktalną krzywą zwaną smokiem Heighwaya. Smoczą
krzywą możemy więc traktować jako aproksymację smoka.

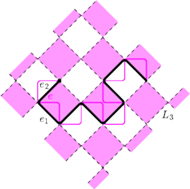
Rys. 4 Siatka
 pomalowana w „szachownicę”. Na czarno zaznaczono krzywą
pomalowana w „szachownicę”. Na czarno zaznaczono krzywą
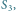 kolorem – krzywą
kolorem – krzywą
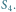
Teraz już jesteśmy gotowi do dowodu faktu, że smocza krzywa nie ma
samoprzecięć. Dowód przytaczamy za Geraldem Edgarem [1]. Narysujmy
krzywą
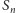 na kwadratowej siatce
na kwadratowej siatce
 o długości krawędzi
o długości krawędzi
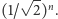 Każdy odcinek krzywej pokrywa się z jedną krawędzią siatki.
Ponadto pomalujmy kwadraty siatki
Każdy odcinek krzywej pokrywa się z jedną krawędzią siatki.
Ponadto pomalujmy kwadraty siatki
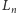 w „szachownicę” (Rys. 4).
Zauważmy, że gdy konstruujemy krzywą
w „szachownicę” (Rys. 4).
Zauważmy, że gdy konstruujemy krzywą
 to rysujemy trójkąty
naprzemiennie na kolorowych i białych kwadratach. Ponadto wszystkie
trójkąty konstruowane na kolorowych polach pochodzą od odcinków
to rysujemy trójkąty
naprzemiennie na kolorowych i białych kwadratach. Ponadto wszystkie
trójkąty konstruowane na kolorowych polach pochodzą od odcinków
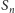 równoległych do jednej z osi siatki
równoległych do jednej z osi siatki
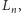 a trójkąty
konstruowane na białych polach pochodzą od odcinków równoległych do
drugiej osi.
a trójkąty
konstruowane na białych polach pochodzą od odcinków równoległych do
drugiej osi.
Ponieważ w każdym wierzchołku siatki krzywa ma kąt prosty (który,
być może, dotyka drugiego kąta prostego w tym wierzchołku), zatem aby
uzyskać samoprzecięcie, któraś z krawędzi siatki musiałaby należeć do
krzywej dwukrotnie jako jej odcinek. Załóżmy zatem, że w
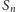 nie ma
takiego odcinka; pokażemy, że wynika z tego, iż w
nie ma
takiego odcinka; pokażemy, że wynika z tego, iż w
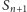 również
takiego nie ma. Niech
również
takiego nie ma. Niech
 będzie dowolnym kwadratem w siatce
będzie dowolnym kwadratem w siatce
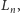
 – krawędzią siatki
– krawędzią siatki
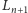 wewnątrz
wewnątrz
 a
a
 i
i
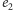 – krawędziami siatki
– krawędziami siatki
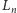 o wspólnym
wierzchołku z
o wspólnym
wierzchołku z
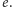 Krzywa
Krzywa
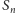 odwiedza każdą z krawędzi
odwiedza każdą z krawędzi
 co najwyżej raz, a krzywa
co najwyżej raz, a krzywa
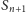 odwiedza krawędź
odwiedza krawędź
 dokładnie raz dla każdego trójkąta skonstruowanego na
dokładnie raz dla każdego trójkąta skonstruowanego na
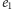 lub
lub
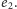 Ale ponieważ te dwie krawędzie są prostopadłe, wobec tego tylko na
jednej z nich możemy zbudować trójkąt w kwadracie
Ale ponieważ te dwie krawędzie są prostopadłe, wobec tego tylko na
jednej z nich możemy zbudować trójkąt w kwadracie
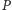 – na tej,
która jest kompatybilna z kolorem kwadratu
– na tej,
która jest kompatybilna z kolorem kwadratu
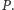 To kończy dowód.
To kończy dowód.

Rys. 5 Cztery nieskończone smocze krzywe wypełniające płaszczyznę.

Rys. 6 Smok Heighwaya jest sumą dwóch swoich kopii o rozłącznych wnętrzach, przy
podobieństwie o skali
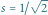
Równie ciekawy jest fakt następujący: jeśli narysujemy cztery nieskończone
smocze krzywe mające swoje początki w tym samym punkcie, ale obrócone
o wielokrotności
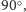 to nie tylko nie będą się one ze sobą przecinać,
ale, co więcej, pokryją całą płaszczyznę (tzn. każda jednostkowa krawędź
siatki będzie należeć do jednej z krzywych; Rys. 5). Dowód tego faktu
jest trudniejszy – zainteresowanych Czytelników odsyłamy do artykułu
Chandlera Davisa i Donalda Knutha [2], opisującego zaskakujące związki
smoczych krzywych z systemami pozycyjnymi o podstawie zespolonej.
Swoją drogą, Knuth, jako prawdziwy fan smoczej krzywej, ma w domu na
ścianie krzywą
to nie tylko nie będą się one ze sobą przecinać,
ale, co więcej, pokryją całą płaszczyznę (tzn. każda jednostkowa krawędź
siatki będzie należeć do jednej z krzywych; Rys. 5). Dowód tego faktu
jest trudniejszy – zainteresowanych Czytelników odsyłamy do artykułu
Chandlera Davisa i Donalda Knutha [2], opisującego zaskakujące związki
smoczych krzywych z systemami pozycyjnymi o podstawie zespolonej.
Swoją drogą, Knuth, jako prawdziwy fan smoczej krzywej, ma w domu na
ścianie krzywą
 ułożoną z 986 własnoręcznie wypalonych
ceramicznych kafelków.
ułożoną z 986 własnoręcznie wypalonych
ceramicznych kafelków.
Czytelnik, który przeczytał artykuł Krzysztofa Barańskiego w tym numerze,
może pokusić się o obliczenie wymiaru fraktalnego smoka Heighwaya. Jak
pokazaliśmy, smocza krzywa ma strukturę rekurencyjną: składa się z dwóch
krzywych mniejszych rzędów. Tak więc na
 składają się dwie kopie
składają się dwie kopie
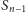 przeskalowane o czynnik
przeskalowane o czynnik
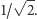 Z tego wynika podobna
własność smoka Heighwaya: jest on sumą dwóch swoich kopii o rozłącznych
wnętrzach, przy podobieństwie o skali
Z tego wynika podobna
własność smoka Heighwaya: jest on sumą dwóch swoich kopii o rozłącznych
wnętrzach, przy podobieństwie o skali
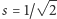 (Rys. 6). To powoduje,
że wymiar smoka
(Rys. 6). To powoduje,
że wymiar smoka
 musi spełniać równanie
musi spełniać równanie

Miłośników parkietaży ucieszy zapewne fakt, że smokiem można pokryć płaszczyznę – i to na wiele sposobów!
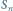 jest krzywa rzędu
jest krzywa rzędu

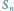 (linia ciągła) na krzywej
(linia ciągła) na krzywej
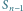 (linia
przerywana).
(linia
przerywana).
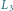 pomalowana w „szachownicę”. Na czarno zaznaczono krzywą
pomalowana w „szachownicę”. Na czarno zaznaczono krzywą
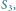 kolorem – krzywą
kolorem – krzywą