Wzór Eulera i balony
Polski namiot na francuskim Festiwalu Nauki był tak pełen gości, że miejsce dla jego matematycznej części życzliwie zostało ofiarowane przez Jeana Brette’a i jego kolegów w namiocie Pałacu Odkryć.
W ten sposób młodzi Francuzi odwiedzający namiot matematyczny nie tylko rozwiązywali łamigłówki, ale też nadmuchiwali balony z polskimi emblematami, rysowali na nich kropki oraz kreski i poznawali genialne odkrycie Kartezjusza i Eulera.
Małe baloniki
Narysujmy na baloniku kropki i kreski, trzymając się następujących reguł:
- •
- końce każdej z kresek oznaczone są kropkami;
- •
- każde dwie kropki połączone są linią złożoną z kresek;
- •
- kreski się nie przecinają.
W trakcie rysowania powstają zazwyczaj na baloniku ograniczone kreskami pola. W dalszym ciągu interesować nas będzie, ile wynosi wartość następującego wyrażenia:

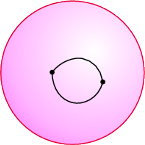
Narysujmy najpierw jedną kropkę na baloniku (Rys. 1) i obliczmy
 .
Mamy oczywiście jedną kropkę, jedno duże pole (powierzchnia balonu) i zero
kresek, więc
.
Mamy oczywiście jedną kropkę, jedno duże pole (powierzchnia balonu) i zero
kresek, więc

Rysujemy dalej. Możemy teraz tylko dorysować kreskę i zakończyć ją
kropką (Rys. 2). Wartość liczby
 nie zmieni się:
nie zmieni się:

Następnie
- •
- albo znów dorysujemy kreskę z nową kropką na końcu (Rys. 3) i wartość
 nie zmieni się, bo wtedy
nie zmieni się, bo wtedy 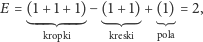
- •
- albo dorysujemy kreskę ze starą kropką na końcu (Rys. 4) i wtedy też
wartość
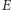 nie ulegnie zmianie, gdyż powstanie nowe pole
i otrzymamy
nie ulegnie zmianie, gdyż powstanie nowe pole
i otrzymamy 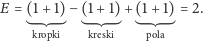
Łatwo uwierzyć, że jakkolwiek byśmy kombinowali, to trzymając się reguł gry, nie
zmienimy wartości liczby
 . Z naszych rozważań wynika zatem
następujące
. Z naszych rozważań wynika zatem
następujące
Twierdzenie. Jeżeli spójny (czyli „jednokawałkowy”) rysunek złożony
z
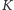 kresek i
kresek i
 kropek na końcach kresek namalowany
na baloniku wycina na nim
kropek na końcach kresek namalowany
na baloniku wycina na nim
 pól, to liczba
pól, to liczba

jest równa 2.
Średnie baloniki
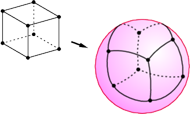
Weźmy teraz do ręki model sześcianu, czworościanu czy dwudziestościanu foremnego i zliczmy jego ściany, wierzchołki i krawędzie. Następnie obliczmy tzw. liczbę Eulera
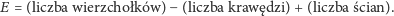 | (1) |
Rys. 5
W każdym przypadku
 Teraz zaczyna być jasne, że liczba
Teraz zaczyna być jasne, że liczba
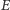 ze średnich i małych baloników to ta sama „osoba”, a nie kolizja
oznaczeń... Dlaczego? Zauważmy, że gdyby nasze modele wielościanów
(dokładniej: modele powierzchni wielościanu) zrobione były z odpowiedniej
gumy, to po nadmuchaniu takiego wielościanu (Rys. 5) uzyskalibyśmy balon
z rysunkiem złożonym z kropek (wierzchołków), kresek (krawędzi) i pól
(ścian). Z poprzedniego twierdzenia uzyskujemy zatem natychmiast nowe
twierdzenie o wielościanach.
ze średnich i małych baloników to ta sama „osoba”, a nie kolizja
oznaczeń... Dlaczego? Zauważmy, że gdyby nasze modele wielościanów
(dokładniej: modele powierzchni wielościanu) zrobione były z odpowiedniej
gumy, to po nadmuchaniu takiego wielościanu (Rys. 5) uzyskalibyśmy balon
z rysunkiem złożonym z kropek (wierzchołków), kresek (krawędzi) i pól
(ścian). Z poprzedniego twierdzenia uzyskujemy zatem natychmiast nowe
twierdzenie o wielościanach.
Czy jednak rzeczywiście wzór
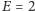 (zwany wzorem Eulera) jest
słuszny dla każdego wielościanu?
(zwany wzorem Eulera) jest
słuszny dla każdego wielościanu?
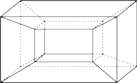
Rozważmy wielościan w kształcie ramy obrazu (Rys. 6). Mamy tutaj 16 ścian (8 prostokątów i 8 trapezów), 16 wierzchołków i 32 krawędzie. A zatem

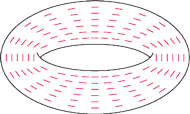
No i klęska ... Nasze twierdzenie jest fałszywe?! Niezupełnie. Zauważmy bowiem, że nadmuchując gumową ramę obrazu nie uzyskamy zwykłego „sferycznego” balonika, ale gumową dętkę. Na gumowej dętce nie da się już jednak przeprowadzić takiego samego dowodu jak ten z „małych baloników” (patrz Rys. 7).
Z drugiej strony ograniczając się tylko do wypukłych wielościanów, których powierzchnia po nadmuchaniu na pewno jest „sferycznym” balonikiem, uzyskamy
Twierdzenie 1 (Eulera). Dla każdego wypukłego wielościanu liczba Eulera zdefiniowana w równaniu (1) jest równa 2.
Duże baloniki

Rys. 8
Przykład z dętką rowerową nie powinien nikogo zniechęcać. Wręcz przeciwnie:
odkryliśmy, że jest coś, co łączy wszystkie wielościany, których
powierzchnia po nadmuchaniu staje się „sferycznym balonikiem”. Jest to jakaś
magiczna cecha, która odróżnia te wielościany od innych, których
powierzchnia po nadmuchaniu staje się np. gumową dętką. Co więcej, to nie
w naturze wielościanu, ale w naturze balonika leży klucz do sekretu.
A przecież „sferyczny balonik” może przybierać bardzo różne kształty
(Rys. 8), zależnie od tego, jak go ściśniemy. Dla każdego z tych
kształtów będzie jednak spełniony wzór Eulera! Ta obserwacja prowadzi nas
do klasyfikacji baloników ze względu na odpowiadającą im liczbę Eulera.
Łatwo znajdziemy te, dla których liczba Eulera jest równa
 ,
,
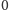 ,
,
 ,
,
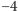 itd...
itd...
I oto jesteśmy o krok od fundamentalnego wyniku.
Twierdzenie (o klasyfikacji zwartych powierzchni dwuwymiarowych). Każda ograniczona dwuwymiarowa powierzchnia bez brzegu, która jest w „jednym kawałku”, i o której można powiedzieć, gdzie ma wewnętrzną, a gdzie zewnętrzną stronę, jest powierzchnią pączka ewentualnie z dziurami w środku.

Rys. 9
Rys. 10

Rys. 11
Rys. 12
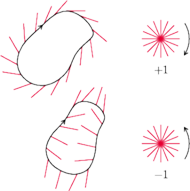
No, dobrze, a czy oprócz policzenia liczby dziur w powierzchni możemy w inny sposób przekonać się o tym, ile jest równa liczba Eulera (tzw. charakterystyka Eulera–Poincarégo) tej powierzchni? Owszem. Można, na przykład, spowodować, by powierzchnia balonika porosła włosami, a następnie gładko balonik uczesać. Dętkę zaczesać można bez żadnej łysinki (Rys. 10), ale ze sferą taka sztuka się nie uda. Na przykład przy zaczesaniu z rysunku 11 mamy dwie łysinki na biegunach. Biorąc wokół każdej łysinki krzywą z określonym odpowiednio kierunkiem ruchu (czasem zgodnie, czasem przeciwnie do ruchu wskazówek zegara – nie będziemy tu wchodzić w szczegóły), możemy obliczyć tzw. indeks łysinki, czyli to, ile obrotów wykonały włoski wzdłuż krzywej (jeśli zgodnie z kierunkiem obrotu zadanym na tej krzywej, to ze znakiem plus, jeśli przeciwnie – to z minusem; Rys. 12). Zachodzi

Rys. 13
Rys. 14
Twierdzenie (Poincaré). Liczba Eulera
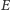 jest równa sumie indeksów
wszystkich łysinek na powierzchni
jest równa sumie indeksów
wszystkich łysinek na powierzchni

Jest to zadziwiające twierdzenie, gdyż łączy ono własność całej powierzchni (liczbę Eulera) z jej własnościami lokalnymi (indeksy łysinek).
Gdyby ktoś nie chciał jednak czesać balonów, może liczbę Eulera
(charakterystykę Eulera–Poincarégo) obliczać jeszcze inaczej, wykorzystując
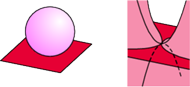
tzw. krzywiznę Gaussa. Żeby zrozumieć, o co chodzi, wyobraźmy sobie,
że nasze baloniki pokryte są sierścią, czyli włoskami długości jeden,
sterczącymi prostopadle do powierzchni. Weźmy teraz punkt
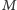 i mały
fragment powierzchni wokół tego punktu o polu
i mały
fragment powierzchni wokół tego punktu o polu
 . Następnie
zbierzmy ostrożnie włoski z tego fragmentu powierzchni i ułóżmy je
tak, by wyrastały z jednego punktu, wciąż zachowując swój dawny
kierunek (Rys. 13). Wolne końce włosków wyznaczą nową niewielką
powierzchnię o polu
. Następnie
zbierzmy ostrożnie włoski z tego fragmentu powierzchni i ułóżmy je
tak, by wyrastały z jednego punktu, wciąż zachowując swój dawny
kierunek (Rys. 13). Wolne końce włosków wyznaczą nową niewielką
powierzchnię o polu
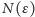 . Możemy teraz określić krzywiznę Gaussa
w punkcie
. Możemy teraz określić krzywiznę Gaussa
w punkcie
 . Jej wartość bezwzględna jest równa granicy
. Jej wartość bezwzględna jest równa granicy

 leży po jej jednej stronie jak deska na piłce,
a z minusem, gdy płaszczyzna ta rozcina powierzchię, jak w przypadku siodła
(Rys. 14).
leży po jej jednej stronie jak deska na piłce,
a z minusem, gdy płaszczyzna ta rozcina powierzchię, jak w przypadku siodła
(Rys. 14).Okazuje się, że krzywizna Gaussa jest ściśle związana z charakterystyką Eulera–Poincarégo. Mówi o tym
Twierdzenie (Gaussa–Bonneta). Sumując (ściślej: całkując) krzywiznę Gaussa
po powierzchni i dzieląc przez
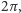 otrzymujemy liczbę Eulera tej
powierzchni
otrzymujemy liczbę Eulera tej
powierzchni

Ci Czytelnicy, którzy nie wiedzą, jak się całkuje po powierzchni, mogą
myśleć w ten sposób: wykonując powierzchnię balonu z papieru
milimetrowego i w każdym milimetrowym kwadraciku wpisując średnią
krzywiznę Gaussa w tym kwadraciku (jednostką jest milimetr), a następnie
sumując wszystkie liczby, otrzymamy z bardzo dobrym przybliżeniem liczbę
Eulera powierzchni balonika pomnożoną przez

W ten sposób od zabawy z balonem i mazakami można dojść do takiej matematyki, która raczej budzi szacunek.