Przestrzenie ilorazowe, czyli sklejanie kartki papieru
Geometria wstęgi Möbiusa
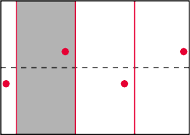
Rys. 9

Rys. 10
Inną, a może nawet lepszą, zabawą z kartką papieru jest zrobienie z niej wstęgi Möbiusa. Przekształcenia, które wykorzystujemy tym razem, to symetrie z poślizgiem: ustalamy prostą na płaszczyźnie oraz równoległy do niej wektor i każdy punkt płaszczyzny przesuwamy o wektor, a potem odbijamy względem prostej (a może na odwrót?). Obszar fundamentalny jest taki sam, jak dla walca, ale orbity punktów nie leżą już na prostej, tylko zawierają punkty nad i pod wybraną osią symetrii (Rys. 9). Oczywiście, z wyjątkiem orbit punktów leżących na samej osi symetrii.
Okazuje się, że na wstędze Möbiusa można wyróżnić jeszcze więcej typów prostych niż na walcu. Oprócz pionowych i spiralnych mamy proste zamknięte dłuższe i krótsze. Prosta pochodząca od osi symetrii jest dwa razy krótsza od wszystkich innych prostych zamkniętych. Można to sprawdzić doświadczalnie, rozcinając jedną wstęgę przez środek, a drugą przy brzegu. Wszystkie rodzaje prostych pokazuje rysunek 10. Widać na nim, na przykład, że proste spiralne mają samoprzecięcia. W szczególności wynika stąd, że piąty postulat Euklidesa nie jest spełniony. Warto jeszcze zauważyć, że tak jak na walcu, przez dwa punkty może przechodzić nieskończenie wiele prostych spiralnych.
O ile na walcu poszczególne okręgi zachowywały się dość stabilnie, teraz już nie jest tak dobrze: proponujemy, na przykład, poszukać dwóch okręgów o tym samym promieniu, ale różnej długości. Natomiast konstrukcja trójkątów niespełniających pierwszej cechy przystawania przebiega podobnie jak poprzednio. Tym razem jednak obydwa trójkąty rozcinają przestrzeń na część ograniczoną i nieograniczoną, więc trzeba zauważyć coś innego, żeby je rozróżnić. Okazuje się, że wystarczy zbadać, w którym z otrzymanych obszarów można zmieścić prostą.
Przesunięcia w dwóch kierunkach
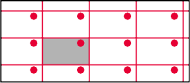
Rys. 11

Rys. 12
Do tej pory zajmowaliśmy się sklejaniem kartki tylko w jednym kierunku. Tym razem do skonstruowania przestrzeni ilorazowej użyjemy przesunięć o wektor poziomy i przesunięć o wektor pionowy. Obszarem fundamentalnym jest prostokąt – utożsamiamy w nim równoległe brzegi. Otrzymana przestrzeń wygląda trochę jak walec, ale obcięty z dwóch stron i sklejony – to jest torus.
Opis prostych zacznijmy od zamkniętych. Oczywiście, jest prosta pionowa i pozioma, ale można też zrobić ukośną, również zamkniętą. Co więcej, możemy skonstruować dowolnie długą prostą zamkniętą. W obszarze fundamentalnym narysujemy ją, dzieląc, na przykład, poziome brzegi na odpowiednio dużo równych części, jak na rysunku 12. Ale mamy też proste nieskończone. Zaznaczmy na dolnym boku prostokąta, mierząc od lewego końca, odcinek o długości niewspółmiernej z długością tego boku (na przykład niewymiernej, jeśli bok ma długość będącą liczbą wymierną). Wraz z lewym bokiem prostokąta ten odcinek utworzy mniejszy prostokąt – przedłużenie jego przekątnej to interesująca nas prosta. Łatwo sprawdzić, że nigdy się nie zamknie i utworzy zbiór gęsty w torusie (czyli jej punkty będą dowolnie blisko każdego punktu). Mimo to zostaje jeszcze na tyle dużo miejsca, żeby można było dołożyć drugą prostą, równoległą do tej, tak aby piąty aksjomat Euklidesa był spełniony!
Ciekawym okręgiem, który można zaobserwować na torusie, jest okrąg będący zbiorem pustym. Wystarczy przyjąć odpowiednio duży promień, a wszystkie punkty przestrzeni będą leżały zbyt blisko środka, by należeć do okręgu. Wobec tego widać też, że cały torus jest bardzo dobrym kołem.
Zauważyliśmy już, że torus możemy otrzymać z rozważanego wcześniej walca przez dodanie przesunięć o pionowe wektory. Możemy sobie wyobrazić to przejście jako wykonanie dwóch poziomych cięć na walcu i sklejenie brzegu ograniczonej części. To oznacza, że konstrukcje, które wykonaliśmy na walcu, więc też wszystkie opisane fenomeny geometrii, przenoszą się na torus: wystarczy wykonać konstrukcję na walcu, obciąć walec tak, żeby nie naruszyć konstrukcji i skleić brzegi. Czytelnik Wnikliwy z pewnością zechce zbadać, czy na torusie można znaleźć jeszcze coś ciekawego, w szczególności zaś odpowie na pytanie, ile punktów przecięcia mogą mieć narysowane na nim dwa okręgi.
Skrzyżowanie torusa ze wstęgą Möbiusa
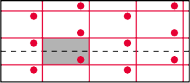
Rys. 13
A gdybyśmy wykonywali przesunięcia o wektor w kierunku pionowym i symetrie z poślizgiem w kierunku poziomym? Tak otrzymana przestrzeń ilorazowa to butelka Kleina. Obszarem fundamentalnym znów jest prostokąt, ale tym razem musimy pamiętać, że w poziomej parze jeden bok przed sklejeniem obracamy. Orbitę pewnego punktu widać na rysunku 13.
Okazuje się, że to też już właściwie przerabialiśmy. Butelkę Kleina możemy sobie wyobrażać jako walec (tym razem z brzegiem), w którym sklejamy części brzegu, ale w innym kierunku, niż żeby dostać torus. A możemy też wyobrazić sobie, że we wstędze Möbiusa (też z brzegiem) dzielimy brzeg na pół i odpowiednio sklejamy. Wszystko zależy od tego, w jakiej kolejności będziemy się przyglądać przekształceniom: symetriom z poślizgiem i przesunięciom. A przyjrzenie się im to ładne ćwiczenie na wyobraźnię wielowymiarową. W każdym razie to, co umiemy skonstruować na walcu i na wstędze, przenosi się na butelkę.
Coś jeszcze?
Do tej pory nie używaliśmy obrotów, czyli nie próbowaliśmy zwinąć kartki w stożek. Czytelnik sprawdzi jednak, że obcinając wierzchołek tak otrzymanego stożka, dostajemy geometrię walca, więc wszystkie konstrukcje, które umiemy wykonać dla walca, przenoszą się na ten przypadek.
Tropienie dalszych fenomenów geometrii przestrzeni ilorazowych pozostawiamy wytrwałym poszukiwaczom przygód.
Felix Klein udowodnił, że każda (dwuwymiarowa) przestrzeń lokalnie euklidesowa powstaje jako taka właśnie przestrzeń ilorazowa i jest tych przestrzeni pięć rodzajów. Podobnie, jako takie przestrzenie ilorazowe otrzymujemy wszystkie przestrzenie lokalnie takie jak sfera, czyli powierzchnia kuli – są ich dwa rodzaje. Wreszcie istnieje jeszcze tylko jedna inna możliwość: to geometrie lokalnie takie, jak ta, którą nazywamy imionami J�anosa Bolyaia i Nikołaja Łobaczewskiego – jak się łatwo domyślić, jest ich nieskończenie wiele rodzajów. Je również uzyskujemy z płaszczyzny Bolyaia-Łobaczewskiego jako przestrzenie ilorazowe.
 ) będą
spełnione, możemy zająć się orbitami. Orbita punktu to wszystkie punkty,
które możemy z tego punktu otrzymać przez zastosowanie przekształceń z
naszego kompletu.
) będą
spełnione, możemy zająć się orbitami. Orbita punktu to wszystkie punkty,
które możemy z tego punktu otrzymać przez zastosowanie przekształceń z
naszego kompletu.
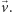 Orbitą każdego punktu będzie z obu stron nieskończony ciąg kropek
leżących na prostej równoległej do
Orbitą każdego punktu będzie z obu stron nieskończony ciąg kropek
leżących na prostej równoległej do
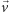 , w którym sąsiednie kropki są
odległe o
, w którym sąsiednie kropki są
odległe o
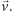 Nietrudno sobie wyobrazić, że gdyby płaszczyzna była z
przezroczystej folii do pakowania kwiatów, to dałoby się ją zwinąć w rulonik,
tak aby wszystkie punkty (każdej!) orbity były widoczne jako jeden punkt (dla
każdej orbity inny).
Nietrudno sobie wyobrazić, że gdyby płaszczyzna była z
przezroczystej folii do pakowania kwiatów, to dałoby się ją zwinąć w rulonik,
tak aby wszystkie punkty (każdej!) orbity były widoczne jako jeden punkt (dla
każdej orbity inny).
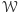 . Otrzymuje się wtedy nową
geometrię.
. Otrzymuje się wtedy nową
geometrię.