Przestrzenie ilorazowe, czyli sklejanie kartki papieru
Do czego może doprowadzić sklejanie kartki papieru?
Geometria walca
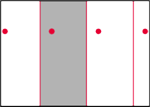
Pierwszą modyfikacją kartki, jaka przychodzi nam do głowy, jest zwinięcie jej w rulonik. Na rysunku 1 szarym kolorem zaznaczony jest obszar fundamentalny przestrzeni ilorazowej wyznaczonej przez wszystkie przesunięcia będące całkowitymi wielokrotnościami pewnego wektora. Kropki to punkty jednej z orbit. Spróbujmy posłużyć się tym rysunkiem dla stwierdzenia, jak wyglądają proste w tej przestrzeni.

Rys. 3

Rys. 4
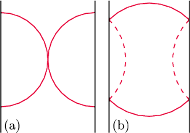
Rys. 5
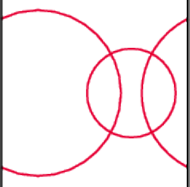
Rys. 6
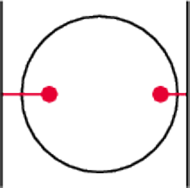
Rys. 7
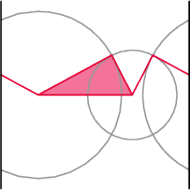
Rys. 8
Okazuje się, że mamy ich trzy różne typy. Pierwszy, czyli prosta pionowa, właściwie nie różni się od prostej na płaszczyźnie. Drugi to prosta zamknięta, która wygląda jak gumka recepturka naciągnięta na walec. Taka prosta ma skończoną długość. Trzeci typ to nieskończona sprężyna.
Jak wiemy, przez dwa punkty na płaszczyźnie przechodzi dokładnie
jedna prosta. Na walcu nie jest to prawda. Wybierzmy na płaszczyźnie
punkty
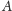 i
i
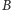 . Dla każdego punktu z orbity punktu
. Dla każdego punktu z orbity punktu
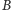 poprowadźmy prostą przez niego i przez
poprowadźmy prostą przez niego i przez
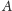 (Rys. 2). Co widzimy na
walcu? Nieskończenie wiele prostych przechodzących przez orbity punktów
(Rys. 2). Co widzimy na
walcu? Nieskończenie wiele prostych przechodzących przez orbity punktów
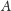 i
i
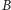 . To ,,sprężyny” o różnych kątach nachylenia do osi walca
(Rys. 3).
. To ,,sprężyny” o różnych kątach nachylenia do osi walca
(Rys. 3).
Nasuwa się pytanie, czy taka geometria jest choć trochę ,,porządna” – sprawdźmy na przykład, czy spełniony jest piąty postulat Euklidesa: do danej prostej, przez dany punkt leżący poza nią, można poprowadzić co najwyżej jedną prostą rozłączną. Okazuje się, że tak: do każdej prostej można dobrać dokładnie jedną prostą tego samego typu równoległą do niej i przechodzącą przez ustalony punkt (Rys. 4). Proste różnych typów nie mogą być równoległe.
Zajmijmy się z kolei okręgami – interesujące są te, które nie mieszczą się w obszarze fundamentalnym. Już okrąg o średnicy równej szerokości obszaru fundamentalnego zaczyna wykazywać nieco dziwne własności. Jest on bowiem styczny sam do siebie (Rys. 5(a)). A jeśli jeszcze trochę zwiększymy promień, to uzyskamy okrąg niespójny. Patrząc na orbity punktów okręgu na płaszczyźnie, które nie zmieściły się w obszarze fundamentalnym, można sobie wyobrazić, że wystające skrzydełka zawiną się do środka. Wobec tego nie zostaną uwzględnione, ponieważ ich odległość od środka okręgu jest mniejsza niż długość promienia (Rys. 5(b)). Okrąg podzieli się na część górną i dolną.
Pewnie nie zdziwi nas już, że dwa okręgi na walcu mogą mieć od zera do czterech punktów wspólnych. Jedną z ciekawych możliwości pokazuje rysunek 6.
Dziwne własności okręgów to jeszcze nic w porównaniu z tym, jak zachowują się na walcu koła. Przyzwyczailiśmy się do myśli, że koło jest figurą wypukłą. A tymczasem na walcu koło może być niewypukłe! Rysunek 7 pokazuje, że każde dwa punkty można połączyć odcinkiem przechodzącym ,,z tyłu” walca. Dla kół o dużych promieniach niektóre z tych odcinków są zawarte w kole, ale zawsze znajdą się takie, które wychodzą poza koło.
Dochodzimy do najważniejszego punktu programu dla walca. Pokażemy, że
nie jest spełniona pierwsza cecha przystawania trójkątów: trójkąty o bokach
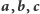 i
i
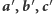 są przystające, jeżeli ich boki są parami
przystające. Konstrukcję kontrprzykładu zaczynamy od narysowania dwóch
okręgów o czterech punktach wspólnych. Pierwszy trójkąt powstaje przez
połączenie ich środków i jednego z punktów przecięcia. Podstawą drugiego
też jest odcinek łączący środki, ale jako trzeci wierzchołek wybieramy drugi
punkt przecięcia okręgów – ten, który leży na poziomej prostej z trzecim
wierzchołkiem pierwszego trójkąta. Efekt widać na rysunku 8. Boki
trójkątów są przystające: jeden jest wspólny, a pozostałe dwa to promienie
obu narysowanych okręgów. Natomiast trójkąty nie są przystające,
chociażby dlatego, że boki jednego rozcinają walec na część ograniczoną
i nieograniczoną, a drugiego na dwie nieograniczone. Zatem nie może istnieć
izometria walca przekształcająca jeden trójkąt na drugi.
są przystające, jeżeli ich boki są parami
przystające. Konstrukcję kontrprzykładu zaczynamy od narysowania dwóch
okręgów o czterech punktach wspólnych. Pierwszy trójkąt powstaje przez
połączenie ich środków i jednego z punktów przecięcia. Podstawą drugiego
też jest odcinek łączący środki, ale jako trzeci wierzchołek wybieramy drugi
punkt przecięcia okręgów – ten, który leży na poziomej prostej z trzecim
wierzchołkiem pierwszego trójkąta. Efekt widać na rysunku 8. Boki
trójkątów są przystające: jeden jest wspólny, a pozostałe dwa to promienie
obu narysowanych okręgów. Natomiast trójkąty nie są przystające,
chociażby dlatego, że boki jednego rozcinają walec na część ograniczoną
i nieograniczoną, a drugiego na dwie nieograniczone. Zatem nie może istnieć
izometria walca przekształcająca jeden trójkąt na drugi.

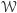 ) będą
spełnione, możemy zająć się orbitami. Orbita punktu to wszystkie punkty,
które możemy z tego punktu otrzymać przez zastosowanie przekształceń z
naszego kompletu.
) będą
spełnione, możemy zająć się orbitami. Orbita punktu to wszystkie punkty,
które możemy z tego punktu otrzymać przez zastosowanie przekształceń z
naszego kompletu.
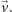 Orbitą każdego punktu będzie z obu stron nieskończony ciąg kropek
leżących na prostej równoległej do
Orbitą każdego punktu będzie z obu stron nieskończony ciąg kropek
leżących na prostej równoległej do
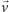 , w którym sąsiednie kropki są
odległe o
, w którym sąsiednie kropki są
odległe o
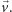 Nietrudno sobie wyobrazić, że gdyby płaszczyzna była z
przezroczystej folii do pakowania kwiatów, to dałoby się ją zwinąć w rulonik,
tak aby wszystkie punkty (każdej!) orbity były widoczne jako jeden punkt (dla
każdej orbity inny).
Nietrudno sobie wyobrazić, że gdyby płaszczyzna była z
przezroczystej folii do pakowania kwiatów, to dałoby się ją zwinąć w rulonik,
tak aby wszystkie punkty (każdej!) orbity były widoczne jako jeden punkt (dla
każdej orbity inny).
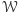 . Otrzymuje się wtedy nową
geometrię.
. Otrzymuje się wtedy nową
geometrię.