Twierdzenia geometrii euklidesowej we Wszechświecie

W artykule rozważymy geometryczny problem, do którego sformułowania użyjemy motywacji astronomicznych. Załóżmy, że chcemy sprawdzić, czy najbliższa naszej intuicji szkolna geometria, zwana geometrią euklidesową, opisuje Wszechświat. Naturalną próbą odpowiedzi będzie eksperymentalne sprawdzenie, czy twierdzenia tej geometrii zachodzą w otaczającej nas przestrzeni. Na przykład możemy zbadać, czy suma kątów wewnętrznych trójkąta utworzonego przez punkt na Ziemi i dwa punkty na różnych odległych gwiazdach wynosi 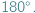 Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
Przyjmujemy, że nasze sprawdzenia dały wynik pozytywny, i zakładamy, że Ziemia nie zajmuje wyróżnionego miejsca we Wszechświecie. Otrzymujemy stąd, że wszystkie twierdzenia geometrii euklidesowej są spełnione dla każdego punktu przestrzeni w jego otoczeniu o pewnym skończonym promieniu. Czy możemy stąd wnioskować, jaka jest geometria Wszechświata? Odpowiedź na to pytanie jest nieoczekiwana. Jeśli ograniczymy nasze rozważania do dwóch wymiarów, by lepiej zrozumieć otrzymaną odpowiedź, to - poza płaszczyzną - istnieją jeszcze cztery typy diametralnie różnych przestrzeni posiadających tę własność.
Na początek rozważmy przykład negatywny, tj. przykład przestrzeni, która nie ma zadanej przez nas własności. Ponieważ żyjemy na powierzchni kuli ziemskiej, to pierwszym kandydatem jest sfera, czyli powierzchnia kuli, na której zbadamy prawdziwość twierdzenia o sumie kątów wewnętrznych trójkąta. Nie wiemy jednak, czym są proste w tej przestrzeni niezbędne do utworzenia trójkąta. W takich przypadkach możemy zaadaptować określenie Archimedesa, który stwierdził, że linie proste w przestrzeni to te, które są lokalnie najkrótsze spośród wszystkich linii łączących dwa dane punkty. Łatwo można się przekonać, że rolę prostych na powierzchni sfery grają okręgi wielkie, czyli takie, które otrzymujemy przez przecięcia sfery płaszczyznami przechodzącymi przez jej środek. Wtedy trójkątem sferycznym możemy nazywać figurę utworzoną z łuków okręgów wielkich. Każdy taki trójkąt ma sumę kątów wewnętrznych większą od 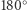 i ta suma zmienia się wraz z wielkością trójkąta, ale jest zawsze większa niż suma kątów wewnętrznych w trójkącie euklidesowym. Oznacza to, że powierzchnia sfery nie ma zadanej przez nas własności. Z tego rozumowania wynika przy okazji, że nie jest możliwe skonstruowanie dokładnej mapy nawet małego fragmentu powierzchni Ziemi.
i ta suma zmienia się wraz z wielkością trójkąta, ale jest zawsze większa niż suma kątów wewnętrznych w trójkącie euklidesowym. Oznacza to, że powierzchnia sfery nie ma zadanej przez nas własności. Z tego rozumowania wynika przy okazji, że nie jest możliwe skonstruowanie dokładnej mapy nawet małego fragmentu powierzchni Ziemi.
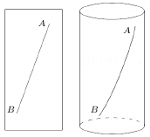
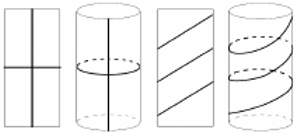
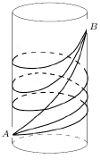
Przejdziemy teraz do opisania cylindra, czyli jednej z czterech przestrzeni, które są obiektem naszego zainteresowania. Cylindrem nazywamy nieskończoną powierzchnię zakreśloną przez prostą obracającą się dookoła innej, ustalonej i równoległej do niej prostej. Linię prostą, którą obracamy, nazywamy tworzącą cylindra. Na cylindrze rozważamy geometrię, której punktami będą punkty cylindra, zaś odległością pomiędzy dwoma punktami będzie długość najkrótszej krzywej leżącej na cylindrze, która łączy te punkty. Nie wiemy jednak, jakie są to krzywe, ale chcemy je wyznaczyć, gdyż zgodnie z określeniem Archimedesa będą to linie proste w geometrii na cylindrze.
W celu opisania tej geometrii wykorzystamy pewną metodę przedstawienia cylindra, która jest oczywista i dobrze znana - przecinamy cylinder wzdłuż tworzącej i otrzymany nieskończony pas rozwijamy na płaszczyznę. Odwrotnie, cylinder otrzymujemy z pasa o równoległych brzegach, wyciętego z płaszczyzny poprzez utożsamienie punktów jego brzegu. Jak widać, takie procedury nie zmieniają długości żadnych krzywych, wobec tego przyjmujemy, że obrazy na cylindrze odcinków prostych leżących w pasie będą odcinkami prostych na cylindrze.
Odcinki prostych na płaszczyźnie możemy łączyć w całe proste. Postępując tak samo na cylindrze, otrzymujemy trzy różne typy prostych. Z rysunków widzimy, że tworzące są jednym z typów prostych na cylindrze, okręgi prostopadłe do tworzących to drugi typ prostych i, na koniec, najciekawszy typ prostych dają linie śrubowe. Łatwo zauważyć, że te proste mają inne własności niż linie proste w geometrii euklidesowej. Jedną z najciekawszych jest ta, że przez dwa dane różne punkty 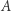 i
i 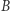 na cylindrze przechodzi więcej niż jedna prosta, ale odcinek tylko jednej z nich minimalizuje długość wszystkich krzywych łączących te punkty.
na cylindrze przechodzi więcej niż jedna prosta, ale odcinek tylko jednej z nich minimalizuje długość wszystkich krzywych łączących te punkty.
Należy także pamiętać, że odległością pomiędzy tymi punktami jest najmniejsza z długości odcinków różnych prostych na cylindrze łączących te punkty. Wynika stąd wprost, że geometria na cylindrze nie jest euklidesowa, gdyż na płaszczyźnie przez dwa dane różne punkty przechodzi dokładnie jedna prosta. Ponadto na cylindrze istnieją zamknięte linie proste - okręgi prostopadłe do tworzących, zaś na płaszczyźnie wszystkie linie proste są niezamknięte.
Na zakończenie uzasadnimy, że na cylindrze w każdym kole o pewnym promieniu geometria jest identyczna z geometrią na płaszczyźnie. Kołem na cylindrze będziemy nazywać figurę, która po rozcięciu cylindra wzdłuż tworzącej nieprzecinającej tej figury przechodzi na zwykłe koło.
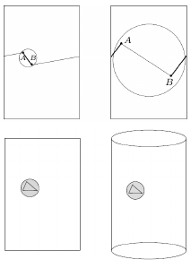
Pozostaje zrozumieć, jak się mierzy odległość na cylindrze, który jest reprezentowany przez rozwinięty pas. Na rysunkach przedstawiono sytuacje, gdy odcinek łączący punkty 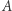 i
i 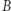 ma długość równą odległości pomiędzy tymi punktami i gdy ma długość różną od tej odległości. Odcinki zaznaczone grubszą linią są odcinkami realizującymi odległość pomiędzy punktami na cylindrze. W drugim przypadku powodem różnicy jest fakt, że kawałek prostej zaznaczonej cieńszą linią nie daje odcinka najkrótszego, a najkrótszym odcinkiem jest odcinek złożony z dwóch odcinków, które po sklejeniu utworzą właściwy najkrótszy odcinek.
ma długość równą odległości pomiędzy tymi punktami i gdy ma długość różną od tej odległości. Odcinki zaznaczone grubszą linią są odcinkami realizującymi odległość pomiędzy punktami na cylindrze. W drugim przypadku powodem różnicy jest fakt, że kawałek prostej zaznaczonej cieńszą linią nie daje odcinka najkrótszego, a najkrótszym odcinkiem jest odcinek złożony z dwóch odcinków, które po sklejeniu utworzą właściwy najkrótszy odcinek.
Rozważmy koło o środku w dowolnym punkcie cylindra i o średnicy mniejszej niż połowa szerokości pasa, z którego jest wykonany cylinder. Jeśli rozetniemy cylinder wzdłuż tworzącej, która nie przecina koła, to dla każdych dwóch punktów z koła ich odległość jest równa długości łączącego je odcinka leżącego w kole. Otrzymujemy więc na cylindrze w dowolnym miejscu koło, w którym zachodzą wszystkie twierdzenia geometrii euklidesowej.
Oznacza to, że nawet jeśli sprawdzimy, że wszystkie twierdzenia geometrii euklidesowej zachodzą w największym możliwym do zbadania otoczeniu Ziemi, to nie możemy stąd wnioskować o globalnej naturze geometrii Wszechświata.
Pozostałe trzy geometrie w przypadku dwuwymiarowym to geometrie na torusie, wstędze Möbiusa i butelce Kleina. Rozważając ten problem w przypadku trójwymiarowym, otrzymujemy osiemnaście różnych typów geometrii odpowiadających na nasze pytanie.