Co to jest?
Przestrzeń metryczna
Jeżeli każdej parze elementów danego zbioru (nazwijmy go 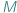 ) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez
) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez 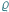 ), to powstanie przestrzeń metryczna
), to powstanie przestrzeń metryczna 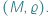
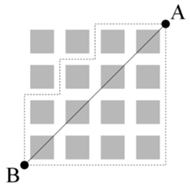
Zauważmy, że w otaczającym nas świecie spotykamy inne sposoby mierzenia odległości niż sugerowany przez Euklidesa. Faktyczna odległość, jaką trzeba pokonać w mieście z punktu 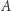 do
do 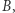 na ogół ma niewiele wspólnego z odcinkiem łączącym te punkty (na rysunku obok szare kwadraty można postrzegać jak budynki, a biała przestrzeń to ulice między nimi). Nawet podróżując samolotem, nie przemieszczamy się nigdy po najkrótszej trasie - nie istnieją podziemne międzykontynentalne tunele. Dodatkowo piloci są zobowiązani do poruszania się tzw. korytarzami, a nie np. wzdłuż okręgu przechodzącego przez Warszawę i Nowy York, którego środkiem jest środek kuli ziemskiej.
na ogół ma niewiele wspólnego z odcinkiem łączącym te punkty (na rysunku obok szare kwadraty można postrzegać jak budynki, a biała przestrzeń to ulice między nimi). Nawet podróżując samolotem, nie przemieszczamy się nigdy po najkrótszej trasie - nie istnieją podziemne międzykontynentalne tunele. Dodatkowo piloci są zobowiązani do poruszania się tzw. korytarzami, a nie np. wzdłuż okręgu przechodzącego przez Warszawę i Nowy York, którego środkiem jest środek kuli ziemskiej.
Odległość przypisana każdej parze elementów ze zbioru 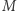 nie może być bylejaka, musi spełniać następujące warunki:
nie może być bylejaka, musi spełniać następujące warunki:
- A.
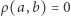 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 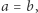
- B.
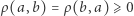 dla dowolnych punktów
dla dowolnych punktów 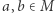 (symetria),
(symetria),- C.
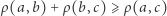 dla dowolnych punktów
dla dowolnych punktów 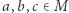 (nierówność trójkąta).
(nierówność trójkąta).
Postulaty te są dosyć naturalne: odległość między 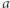 i
i 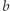 wynosi zero tylko wtedy, gdy
wynosi zero tylko wtedy, gdy 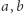 są równe; odległość od
są równe; odległość od 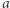 do
do 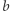 jest równa odległości od
jest równa odległości od 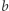 do
do 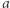 ; odległość od
; odległość od 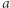 do
do  nie jest większa od sumy odległości od
nie jest większa od sumy odległości od 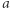 do
do 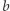 i od
i od 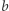 do
do  Przykłady przestrzeni metrycznych:
Przykłady przestrzeni metrycznych:
- 1.
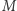 to zbiór liczb rzeczywistych, a odległość dwóch liczb to wartość bezwzględna ich różnicy.
to zbiór liczb rzeczywistych, a odległość dwóch liczb to wartość bezwzględna ich różnicy.- 2.
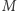 to zbiór punktów płaszczyzny, a metryka
to zbiór punktów płaszczyzny, a metryka 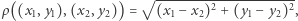 czyli "zwykła" (Euklidesowa) odległość. Nazwa "nierówność trójkąta" w tym wypadku oznacza, że suma dwóch boków trójkąta jest nie mniejsza od trzeciego boku (mimo że w przypadku równości trudno mówić o trójkącie).
czyli "zwykła" (Euklidesowa) odległość. Nazwa "nierówność trójkąta" w tym wypadku oznacza, że suma dwóch boków trójkąta jest nie mniejsza od trzeciego boku (mimo że w przypadku równości trudno mówić o trójkącie).- 3.
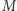 to zbiór punktów płaszczyzny oraz
to zbiór punktów płaszczyzny oraz 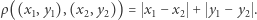 To tzw. metryka miejska. Przemieszczając się z punktu
To tzw. metryka miejska. Przemieszczając się z punktu 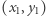 do punktu
do punktu 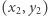 w mieście, w którym każde dwie ulice są albo równoległe, albo prostopadłe, przebywamy w jednym kierunku drogę
w mieście, w którym każde dwie ulice są albo równoległe, albo prostopadłe, przebywamy w jednym kierunku drogę 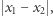 a w prostopadłym
a w prostopadłym 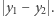 Całkowita odległość to suma długości tych tras. Przykładowe najkrótsze trasy między punktem
Całkowita odległość to suma długości tych tras. Przykładowe najkrótsze trasy między punktem 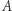 i
i 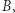 w tej właśnie metryce, zostały przedstawione na rysunku przerywaną linią.
w tej właśnie metryce, zostały przedstawione na rysunku przerywaną linią.- 4.
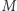 to zbiór punktów płaszczyzny, a
to zbiór punktów płaszczyzny, a 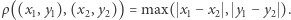
- 5.
- Podzbiór dowolnej przestrzeni metrycznej jest przestrzenią metryczną - mnóstwo przykładów za darmo.
- 6.
- Przestrzenią metryczną jest wstęga Möbiusa (jako podzbiór przestrzeni trójwymiarowej), na której można zdefiniować wiele sposobów mierzenia odległości. Metryką między punktami na tej wstędze może być np. długość najkrótszej (w zwykłym sensie) trasy między nimi, poprowadzonej po powierzchni tej wstęgi.
- 7.
- Niech
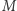 będzie dowolnym zbiorem. Przyjmując, że odległość punktu od siebie równa jest
będzie dowolnym zbiorem. Przyjmując, że odległość punktu od siebie równa jest 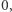 a odległość różnych punktów to
a odległość różnych punktów to 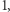 dostajemy tzw. przestrzeń dyskretną.
dostajemy tzw. przestrzeń dyskretną. - 8.
- Niech
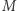 oznacza zbiór wszystkich funkcji ograniczonych o wartościach rzeczywistych (których dziedziną jest
oznacza zbiór wszystkich funkcji ograniczonych o wartościach rzeczywistych (których dziedziną jest 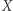 ). Odległość
). Odległość 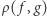 między funkcjami
między funkcjami 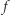 i
i 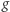 definiujemy jako najmniejsze ograniczenie górne (kres górny) zbioru złożonego ze wszystkich liczb postaci
definiujemy jako najmniejsze ograniczenie górne (kres górny) zbioru złożonego ze wszystkich liczb postaci 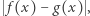 gdzie
gdzie 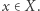 Np. niech
Np. niech ![=[−3,3] |X ,](/math/temat/matematyka/geometria/2019/03/25/Przestrzen_metryczna/37x-a39e794618e81f7c2e5642ff842e2b25a0c69e8e-im-33,33,33-FF,FF,FF.gif) wtedy
wtedy 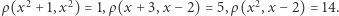
- 9.
- Niech
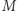 oznacza zbiór złożony ze wszystkich funkcji ciągłych na przedziale
oznacza zbiór złożony ze wszystkich funkcji ciągłych na przedziale ![[a,b],](/math/temat/matematyka/geometria/2019/03/25/Przestrzen_metryczna/40x-a39e794618e81f7c2e5642ff842e2b25a0c69e8e-im-33,33,33-FF,FF,FF.gif) których wartościami są liczby rzeczywiste. Definiujemy metrykę
których wartościami są liczby rzeczywiste. Definiujemy metrykę 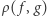 jako pole powierzchni
jako pole powierzchni 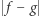 nad przedziałem
nad przedziałem ![|[a, b].](/math/temat/matematyka/geometria/2019/03/25/Przestrzen_metryczna/43x-a39e794618e81f7c2e5642ff842e2b25a0c69e8e-im-33,33,33-FF,FF,FF.gif)
W górach "odległość" podaje się zazwyczaj jako przewidywany czas przejścia trasy - 500 metrów spaceru po płaskim jest dużo "bliżej" niż 500 metrów spaceru pod górę. Zauważmy, że taka górska odległość nie definiuje metryki. Nie jest prawdą, że wejście na Gubałówkę zajmie nam tyle samo czasu, co zejście z niej tą samą trasą (nie zachodzi warunek B).
Metryki z punktów 2, 3, 4 są równoważne, co oznacza, że stwierdzenie 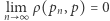 nie zależy od tego, którą z nich mamy na myśli. To samo dotyczy analogicznie zdefiniowanych metryk w przestrzeniach wielowymiarowych. Jeśli rozważymy metryki z punktów
nie zależy od tego, którą z nich mamy na myśli. To samo dotyczy analogicznie zdefiniowanych metryk w przestrzeniach wielowymiarowych. Jeśli rozważymy metryki z punktów 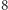 i
i 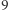 w zbiorze funkcji ciągłych na przedziale
w zbiorze funkcji ciągłych na przedziale ![| [0,2],](/math/temat/matematyka/geometria/2019/03/25/Przestrzen_metryczna/4x-1ad7f34669d225302220e32908295530f1da8ecf-im-33,33,33-FF,FF,FF.gif) to jest już inaczej. Niech
to jest już inaczej. Niech 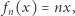 gdy
gdy 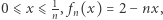 gdy
gdy 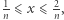 oraz
oraz 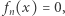 gdy
gdy 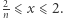 Mamy
Mamy 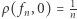 - to pole trójkąta o wysokości
- to pole trójkąta o wysokości 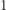 i podstawie
i podstawie 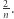
Stąd wynika, że w sensie metryki z przykładu 9. granicą ciągu 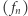 jest funkcja tożsamościowo równa 0. Natomiast odległością funkcji
jest funkcja tożsamościowo równa 0. Natomiast odległością funkcji 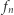 od funkcji tożsamościowo równej zero w sensie metryki z przykładu 8. jest liczba 1, więc ciąg
od funkcji tożsamościowo równej zero w sensie metryki z przykładu 8. jest liczba 1, więc ciąg 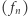 nie jest zbieżny do funkcji zerowej względem tej metryki. Można wykazać, że w tej przestrzeni ciąg
nie jest zbieżny do funkcji zerowej względem tej metryki. Można wykazać, że w tej przestrzeni ciąg 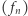 granicy w ogóle nie ma.
granicy w ogóle nie ma.
W przestrzeniach metrycznych prawdziwe są różne twierdzenia o ciągach zbieżnych i funkcjach ciągłych. Można je dowodzić tylko raz, zamiast w każdym przypadku osobno. W istocie rzeczy nie zostały one wymyślone, lecz odkryte. Pojawiały się w dowodach różnych twierdzeń, np. o istnieniu rozwiązań równań algebraicznych, funkcyjnych, różniczkowych - i w końcu podano definicję ogólną.
Przestrzeniami metrycznymi są także butelka Kleina, przestrzenie rzutowe, przestrzenie Łobaczewskiego i wiele, wiele innych.