Zacznijmy od jednego z najbardziej znanych matematyków - to Charles L. Dodgson (1832-1898), student, a później profesor Christ Church College w Oxfordzie. Oczywiście, spieszę uspokoić tych, którzy nie odnajdują w swojej pamięci takiego matematyka: Charles Dodgson nie jest znany jako matematyk i, na dodatek, nie jest znany pod swoim nazwiskiem. To Lewis Carroll, którego dwie książeczki - Alice's Adventures in Wonderland (1865) i Through the Looking Glass (1875) - należą do (przynajmniej europejskiego) kanonu lektur dziecięcych. Pierwsza z nich ma ustaloną polską wersję tytułu: Alicja w krainie czarów, druga zaś znana jest w Polsce pod różnymi tytułami, wśród których jest i Co zobaczyła Alicja po drugiej stronie lustra?

No właśnie - co zobaczyła? Nasuwająca się odpowiedź to: zobaczyła siebie. Każdy jednak, kto np. próbował z pomocą lustra coś sobie obciąć, powiedzmy wąsy albo grzywkę, wie, że napotkamy przy takiej czynności pewne trudności i nasza sprawność sterowania ruchami widzianych w lustrze nożyc jest znacznie naruszona. W ogóle wydaje się, że trzymane w prawej ręce nożyce w lustrze trzymamy w ręce lewej.

Pozwala to postawić hipotezę, że lustro zamienia prawą i lewą stronę. Każdy zresztą chętnie poprze nasz pogląd, uważając przy tym, że wie to od dziecka. Jeśli jednak mamy umysł przenikliwy i zwyczaj zadawania sobie i innym pytania dlaczego?, natychmiast zaczniemy poszukiwać odpowiedzi, dlaczego akurat prawą i lewą, a nie, powiedzmy dół i górę.

Ufni w potęgę poznawczą doświadczeń, możemy wykonać eksperyment: z nagła, aby kompletnie zaskoczyć lustro, obróćmy je o 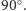Lustro dalej będzie zamieniało prawą i lewą, choć teraz będą one wypadały w tych akurat miejscach lustra, w których poprzednio znajdowały się niezamieniane dół i góra.

I tak pytanie staje się poważne, jak każde pytanie, na które nie umiemy dać zadowalającej odpowiedzi.

Właściwa odpowiedź jest zaskakująca: lustro nie zamienia prawej i lewej. Wydaje się to bzdurą, choć jest prawdą. Zrozumienie tej prawdy jest rzeczą trudną, bo też nie leży ona w optyce, ale głęboko w strukturze używanych przez nas pojęć, właściwie wręcz w filozofii.

Chodzi o to, że używane przez nas pojęcia pochodzą "z różnych szuflad". Każdy przecież uzna, że prostopadłość i posłuszeństwo to pojęcia o różnym pochodzeniu - wywodzą się one z zupełnie odmiennych kręgów doświadczeń. Okazuje się jednak, że różne pochodzenie mogą mieć pojęcia dotyczące tego samego obszaru działania. Dla ilustracji przytoczę trzy przykłady. Pierwszy będzie dotyczył etyki, drugi geografii, a trzeci geometrii.

Przykład I. W okresie największego rozkwitu Starożytnych Aten działała grupa filozofów nazywających się sofistami. Podstawowym kierunkiem ich dociekań było badanie reguł prowadzenia dyskusji. W szczególności interesowało ich, jak można wygrać debatę niezależnie od tego, jakie racje się głosi i jakie racje ma do przedstawienia kontrdyskutant. Swoje przemyślenia potrafili też zastosować praktycznie, udzielając (cóż tu ukrywać - odpłatnie) porad politykom, na co w demokratycznym systemie Aten było duże zapotrzebowanie. Sofistą - należącym do końcowego okresu ich działalności - był Sokrates. Jego końcowa konkluzja była taka, że gdy za przesłanki naszego wywodu przyjmiemy jedno stwierdzenie z zakresu prawa naturalnego i drugie stwierdzenie z zakresu prawa moralnego, wówczas będziemy mogli uzasadnić zupełnie dowolną tezę. Na przykład, jeśli w debacie będziemy powoływać się z jednej strony na wolny rynek i konkurencję, a z drugiej na solidarność międzyludzką i miłość bliźniego, uda się nam bez trudu uzasadnić wszystko, co tylko się komu zamarzy. Można to zresztą zaobserwować w dyskusjach naszych dzisiejszych polityków. Nie byliby oni jednak zadowoleni z powyższego stwierdzenia. Niezadowoleni byli też politycy współczesnych Sokratesowi Aten, więc oskarżyli go o bezbożność i demoralizację młodzieży. Skazali go następnie na śmierć, każąc mu wypić kielich cykuty, co też uczynił.

Przykład II. Dla określenia swojego położenia na kuli ziemskiej żeglarz musi stwierdzić, na jakiej szerokości i długości geograficznej się znajduje. Szerokość geograficzna w pogodną noc daje się łatwo określić - jest to bowiem pojęcie przyrodnicze: wystarczy stwierdzić, jaki kąt z poziomem tworzy kierunek ku Gwieździe Polarnej. Ten kąt to właśnie szerokość geograficzna na naszej półkuli. Nie ma natomiast doświadczenia przyrodniczego pozwalającego określić długość geograficzną. Już sam południk zerowy jest ustalany umownie - do pierwszej wojny światowej były zresztą trzy takie umowy: brytyjska z południkiem zerowym przechodzącym przez londyńskie przedmieście Greenwich, francuska z zerowym południkiem przez Paryż (mam nawet globus z tak zaznaczonym południkiem zerowym) i hiszpańska - przez Kadyks. Dziś powszechnie przyjmuje się tę pierwszą umowę. Do określenia długości geograficznej (nawet przez GPS!) potrzebna jest znajomość różnicy czasu astronomicznego z Greenwich (np. kiedy jest południe) - ta różnica czasu w godzinach pomnożona przez 15 daje długość geograficzną w stopniach (wschodnią, jeśli nasz zegar jest szybszy od londyńskiego, a zachodnią, gdy jest wolniejszy). W czasach, gdy nie było dostatecznie dokładnych zegarów, kłopoty z ustalaniem długości geograficznej były bardzo poważne (posługiwano się tzw. tablicami astronomicznych efemeryd). Stąd w XVII wieku admiralicje posiadających największe floty Anglii i Holandii ufundowały wielką nagrodę za skonstruowanie morskiego chronometru, co nie udało się mimo starań ani Galileuszowi, ani Huygensowi. Dopiero John Harrison taki chronometr skonstruował i ten przy niewielkich zmianach dotrwał do pojawienia się radia. Inna rzecz, że Harrison musiał przez blisko 20 lat procesować się ze skąpymi admirałami, zanim nagrodę uzyskał.

Przykład III. Jeśli chcemy opisać rozwartość jakiegoś kąta, wystarczy podać, jaką część (właściwą lub nie) kąta pełnego on stanowi. Rozwartość kąta pełnego możemy opisać na różne sposoby: a to, że jest to 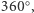a to, że 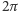radianów, a to, że 400 gradusów (jak chciała Rewolucja Francuska), a to, że 6 000 tysięcznych (jak chcą artylerzyści) i to wyznaczy rozwartość naszego kąta. Tak czy owak możemy poinformować o rozwartości kąta, nie odwołując się do żadnego materialnego wzorca. Ten fakt określamy, mówiąc, że kąt ma miarę naturalną. Natomiast odcinek nie ma miary naturalnej i, aby podać jego długość, obok podania jakiejś liczby musimy odwołać się do jakiegoś materialnego wzorca. Za czasów mojej młodości była to szyna z dwoma nacięciami przechowywana w Sévres pod Paryżem.

Wróćmy do Alicji. Spróbujmy - pamiętając, że mamy różne możliwości - przyjrzeć się pochodzeniu rozmaitych charakterystycznych kierunków jej ciała (wstydliwi mogą, oczywiście, przyglądać się sobie).

Góra i dół są pojęciami przyrodniczymi. Zarówno fizyka (ciążenie), jak wynikająca stąd anatomia (nogi u dołu, głowa u góry) wyraźnie różnicę góry i dołu wyznaczają.

Przód i tył - też są przyrodnicze, bo każdy z nas coś innego ma z przodu (np. nos) niż z tyłu.

Natomiast lewa i prawa to tylko konwencja. Do dwóch strzałek prostopadłych dobieramy trzecią - można to zrobić na dwa równoważne sposoby. Arbitralność widać w trudnościach, jakie mają dzieci (często do późnej starości) z nauczeniem się, gdzie jest prawo, a gdzie lewo - chodzi o czystą umowę: tego nie można zrozumieć, tego trzeba się nauczyć na pamięć. A żarty w rodzaju; lewa ręka to ta, gdzie kciuk jest z prawej strony tylko ową arbitralność podkreślają.

Do tej umowy wrócimy za chwilę, ale teraz zakończmy sprawę z lustrem:
- góry i dołu zmienić nie może;
- przód i tył, oczywiście, zamienia: nie zwróciliśmy na to uwagi, ale przecież stoimy ze swoim odbiciem nos w nos; zmienia strzałkę skierowaną do lustra na skierowaną od lustra;
- prawej i lewej też nie zmienia: przecież ręka z zegarkiem jest z tej samej strony, co była; to my zmieniamy jej nazwę!

I tu pojawia się matematyczne pojęcie orientacji. Jest to kolejność wzajemnie prostopadłych strzałek. Wybór tej kolejności to orientacja przestrzeni. I tu zdumiewający fakt: zarówno w jedno-, jak w dwu-, trój- i więcej wymiarowej przestrzeni jest tyle samo orientacji - dwie. Czyli w dowolnie wymiarowej przestrzeni każdy zestaw maksymalnej liczby wzajemnie prostopadłych strzałek z ustaloną kolejnością daje się przemieścić tak, że się nałoży na jeden z ustalonych dwu takich zestawów. Utarło się, że o jednej orientacji mówimy dodatnia, a o drugiej - ujemna. W przestrzeni trójwymiarowej funkcjonują też techniczne nazwy: prawoskrętna i lewoskrętna.

Matematycznie obie orientacje są równoważne. Ale w szkole - gdzie wszystko musi być jednoznacznie zadekretowane, ustalono, by nazywać je niejako geograficznie: dodatnia (prawoskrętna) orientacja to wschód-północ-góra, na płaszczyźnie wschód-północ i na prostej wschód. Ale nic by się nie zmieniło, gdybyśmy się umówili odwrotnie.

Powstaje pytanie, czy przyroda - jak matematyka - jest wobec tych równoprawnych możliwości sprawiedliwa. A odpowiedź jest - nie. Sprawa ma jednak różne oblicza.

Zacznijmy od siebie - było takie hasło wyborcze: serce masz po lewej stronie, a po prawej masz wątrobę. I przeważnie istotnie tak jest. Skąd biorą się takie nieregularności?

Nierównoprawność w wyborze orientacji przez przyrodę dostrzeżono dawno. Najbardziej oczywistym przykładem są muszle ślimaków - rzeczywiście przytłaczająca większość z nich odpowiada orientacji prawoskrętnej. Od pół wieku objaśnia się to tak: jakakolwiek nierównomierność wzrostu muszli - z jednej strony troszeczkę szybciej niż z drugiej - powoduje jej kształt spiralny; proces ten pogłębił się podczas upływu pokoleń, bo odchylenia się genetycznie przekazywały, a w wyniku ewolucji jedna z orientacji stała się dominująca.

Odkrycie helisy DNA (też praktycznie zawsze o tej samej orientacji) nie zmieniło poglądu na tę sprawę - po prostu jedna z orientacji wygasła.

Asymetria jest też w chemii - tam zamiast o orientacji mówi się o chiralności. Złożone związki organiczne mają bardzo skomplikowaną strukturę przestrzenną i mogą istnieć w wersjach o odmiennej chiralności (czyli orientacji). Okazuje się, że ma to wielkie znaczenie, gdy zostają wchłonięte przez żywy organizm - pożywne substancje w wersji o odmiennej chiralności niejednokrotnie stają się truciznami. Stąd znaczenie kontrolowania chiralności przy produkowaniu substancji odżywczych czy też zwłaszcza lekarstw. Oczywiście, nie zawsze substancja odmienna chiralnie od miłej nam musi być dla nas niemiła: przykładem są zapachy cytrynowy i pomarańczowy, które są swymi lustrzanymi odbiciami.

Znaczenie chiralności zostało podkreślone przyznaniem w 2001 roku Nagrody Nobla właśnie za chirality-controlled synthesis (chiralność i po angielsku jest chiralnością, bo to słowo pochodzi z greki i oznacza rękę - patrz żart o kciuku). Otrzymali ją Wiliam S. Knowles, Ryoji Nyori i K. Barry Sharpless.

Jeśli pod turystycznym kompasem położymy miedziany drucik w kierunku wskazywanym przez igłę magnetyczną i przez ten drucik przepuścimy prąd (wystarczy paluszek AA), to igła odchyli się. Gdy zmienimy bieguny paluszka (czyli prąd "popłynie w przeciwną stronę"), to igła odchyli się też w przeciwną stronę niż poprzednio. Zatem orientacja pary (przepływ prądu - odchylenie igły) będzie znów taka sama.

O sytuacjach, w których przy zmianach zachowywana jest orientacja, mówimy, że "niosą" orientację. Nie wątpię, że Czytelnik Sprytny wskaże bez trudu wiele sytuacji, które niosą orientację i wiele takich, które nie niosą.

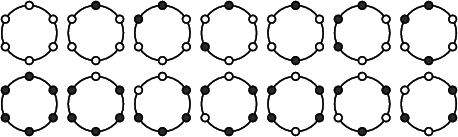
W geometrii łatwo wskazać zarówno obiekty, które niosą na sobie orientację (np. kostka do gry), jak i te, które nie niosą (np. kula). Nie każdy od razu domyśli się, że malując dwoma kolorami "zegar pięciogodzinny", nie można uzyskać obrazka niosącego orientację.

"Sześciogodzinny" zegar już można tak pomalować, by dwa spośród tych "zegarów" (które?) niosły na sobie orientację.

Lustrzany czworokąt już nie pasuje do parkietu

Orientację niesie na sobie każdy czworokąt różnoboczny, o czym przekonuje rysunek na marginesie. Czytelnik Domyślny zauważy, że patrząc na niego, można odkryć przepis na ułożenie parkietu z dowolnych jednakowych czworokątnych płytek (jaki to przepis?).

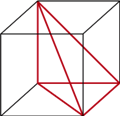
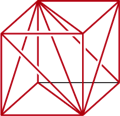
Podobne, a może jeszcze bardziej złożone mogą być sytuacje w przestrzeni. Czworościan widoczny poniżej na rysunku z lewej to (jak każdy Czytelnik Dokładny obliczy) jedna szósta sześcianu, w którym został zbudowany. Nie można jednak z jego sześciu egzemplarzy złożyć tego sześcianu. Jak pokazuje rysunek środkowy, trzy z nich muszą być jego lustrzanymi odbiciami.

Mimo to same takie czworościany o jednakowej orientacji mogą szczelnie wypełnić przestrzeń, o czym przekonuje rysunek prawy: takimi pochylonymi graniastosłupami każdy potrafi "wyparkietować" całą trójwymiarową przestrzeń.

Oczywiście, sześcian nie niesie na sobie orientacji, podobnie jak żaden z pozostałych czterech wielościanów foremnych, czyli platońskich. Natomiast wśród wielościanów półforemnych, czyli archimedesowych (to takie, których ściany są wielokątami foremnymi niekoniecznie jednakowymi, ale naroże w każdym wierzchołku jest takie samo) już takie są. Na marginesie narysowana jest siatka wielościanu archimedesowego, w którego każdym wierzchołku zbiegają się cztery trójkąty równoboczne i kwadrat (to ile jest tych trójkątów?). Jeśli skleimy tę siatkę tak, aby widoczne były pokolorowane ściany kwadratowe, i drugi raz, tak by kolory schowały się w środku, otrzymamy dwa różne, choć lustrzane wielościany - każdy z nich niesie więc orientację.

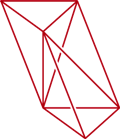
Naturalne kryształy o odmiennej orientacji

Natura sama też potrafi "skleić" wielościan niosący orientację na dwa sposoby. Obok mamy zdjęcie dwóch kryształów kwarcu, będących swymi odbiciami lustrzanymi. Tym, jakie kryształy niosą na sobie orientację i jakie w ogóle są możliwe, a także tym, czy Natura wykorzystuje wszystkie matematycznie dopuszczalne możliwości, zajmuje się leżąca na pograniczu matematyki i geologii krystalografia. Ale o niej innym razem.

---