Jak długa jest kula?
Wyobraźmy sobie, że wewnątrz trójkąta 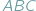 umieściliśmy trójkąt
umieściliśmy trójkąt 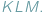 Wówczas pole
Wówczas pole 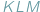 nie przekracza, oczywiście, pola
nie przekracza, oczywiście, pola 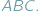 Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta
Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta 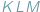 nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 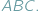
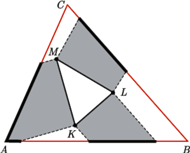
Jeden ze sposobów uzasadnienia tego faktu jest następujący: dla każdego boku trójkąta 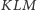 wyobraźmy sobie słońce świecące prostopadle do wybranego boku, umiejscowione po stronie pozostałej części trójkąta
wyobraźmy sobie słońce świecące prostopadle do wybranego boku, umiejscowione po stronie pozostałej części trójkąta 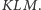 Wówczas na brzegu trójkąta
Wówczas na brzegu trójkąta 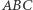 pojawią się rozłączne cienie boków trójkąta
pojawią się rozłączne cienie boków trójkąta 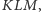 o długościach nie mniejszych od długości odpowiadających im boków
o długościach nie mniejszych od długości odpowiadających im boków 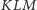 (rysunek obok powinien rozjaśnić wszelkie niejasności tego słonecznego opisu).
(rysunek obok powinien rozjaśnić wszelkie niejasności tego słonecznego opisu).

Dla tych, którzy mają cień wątpliwości, dodatkowe wyjaśnienie: odcinek 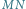 musi być tak krótki, by zmieścił się w czworościanie
musi być tak krótki, by zmieścił się w czworościanie 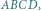 mimo, iż krawędzie
mimo, iż krawędzie 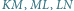 i
i 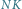 są tylko niewiele krótsze od krawędzi
są tylko niewiele krótsze od krawędzi 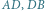 i
i 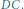
Czy przedstawiona własność przysługuje również innym wielokątom? Chwila namysłu pozwala stwierdzić, że nie - jeśli wewnętrzny wielokąt jest dostatecznie "połamany", jego obwód może śmiało przewyższyć obwód wielokąta zewnętrznego. Nietrudno jednak naprawić tę przykrość, gdyż wystarczy zażądać, aby rozważane wielokąty były wypukłe i wówczas przedstawiony wcześniej argument o "rozłączności cieni" pozostaje w mocy.
Skoro tak dobrze poszło nam na płaszczyźnie, spróbujmy naszych sił w trzech wymiarach. Jeśli pewien wielościan wypukły jest zawarty w innym, to objętość zawartego jest nie większa od objętości zawierającego. Odnośnie pól powierzchni tych wielościanów, możemy zastosować rozumowanie analogiczne do dwuwymiarowego - teraz rozłączne cienie będą rzucane przez ściany wewnętrznego wielościanu (ponownie kluczowe jest założenie o wypukłości rozważanych obiektów). Kolejnym naturalnym zadaniem jest porównanie sumy długości krawędzi bohaterów naszych rozważań. Zapewne, nawet jeśli nie spotkałeś się wcześniej, Czytelniku, z tym problemem, zdążyłeś już pewnie kątem oka dostrzec rysunek na marginesie, który bez cienia wątpliwości dowodzi, że sumy długości krawędzi wielościanów - nawet wypukłych - nie porównują się już w sposób tak elegancki, jakby sugerowały to nasze wcześniejsze przemyślenia. Czy istnieje sposób na uratowanie choćby części naszych przypuszczeń?
Okazuje się, że tak! Wystarczy każdej krawędzi badanych wielościanów przypisać wagę równą zewnętrznemu kątowi między ścianami spotykającymi się wzdłuż tej krawędzi. Aby się o tym przekonać, rozpoczniemy od słynnego zadania o żyrafie, którym bawione są kolejne pokolenia uczniów. Brzmi ono następująco: wybieg dla żyrafy jest otoczony płotem w kształcie trapezu o obwodzie 100 metrów i polu 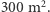 Żyrafa ma szyję długości dwóch metrów i bardzo duży apetyt; oblicz pole powierzchni obszaru znajdującego się w zasięgu żyrafiej paszczy.
Żyrafa ma szyję długości dwóch metrów i bardzo duży apetyt; oblicz pole powierzchni obszaru znajdującego się w zasięgu żyrafiej paszczy.


Na pierwszy rzut uczniowskiego oka problem wydaje się mieć podejrzanie mało założeń, chwila analizy rysunku na marginesie pozwala jednak stwierdzić, że istotnie żadnej innej informacji nam do szczęścia nie potrzeba. Dostępny dla żyrafy obszar spoza wybiegu można podzielić na prostokąty o wysokości 2 i podstawach będących którymś z boków wybiegu oraz fragmenty kół o promieniu 2 i środkach w wierzchołkach wybiegu. Suma pól wspomnianych prostokątów to przemnożony przez 2 obwód wybiegu, czyli 200, fragmenty kół natomiast sumują się do pola całego koła o promieniu 2, czyli 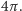 Ostateczna odpowiedź na pytanie to
Ostateczna odpowiedź na pytanie to 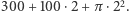 Warto zauważyć, że przedstawione rozumowanie pozostaje słuszne, jeśli o wybiegu założymy tylko, że jest wielokątem wypukłym - dzięki temu wymienione wcześniej części badanego obszaru są rozłączne, a odpowiednie fragmenty kół składają się na jedno pełne koło.
Warto zauważyć, że przedstawione rozumowanie pozostaje słuszne, jeśli o wybiegu założymy tylko, że jest wielokątem wypukłym - dzięki temu wymienione wcześniej części badanego obszaru są rozłączne, a odpowiednie fragmenty kół składają się na jedno pełne koło.
Popuśćmy teraz wodze fantazji i wyobraźmy sobie żyratoperze, czyli żyrafy fruwające radośnie w powietrzu dzięki ogromnym, nietoperzowym skrzydłom. Wybieg dla żyratoperzy to ogromny, wiszący w powietrzu druciany wielościan 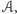 o "okach" pozwalających żyratoperzom na przeciśnięcie ich szyi o długości
o "okach" pozwalających żyratoperzom na przeciśnięcie ich szyi o długości 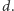 Tym razem obszar, z którego żyratoperze mogą podjadać smakołyki, można podzielić na sam wybieg, prostopadłościany o wysokości
Tym razem obszar, z którego żyratoperze mogą podjadać smakołyki, można podzielić na sam wybieg, prostopadłościany o wysokości 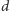 i podstawach będących ścianami wybiegu, fragmenty walców, których wysokości to krawędzie wybiegu, a podstawy to wycinki koła o promieniu
i podstawach będących ścianami wybiegu, fragmenty walców, których wysokości to krawędzie wybiegu, a podstawy to wycinki koła o promieniu 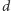 oraz fragmenty kul o środkach w wierzchołkach wybiegu i promieniu
oraz fragmenty kul o środkach w wierzchołkach wybiegu i promieniu 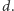
Podobnie jak poprzednio, objętości wspomnianych prostopadłościanów sumują się do powierzchni wielokąta pomnożonej przez 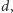 natomiast objętości fragmentów kul - do objętości całej kuli o promieniu
natomiast objętości fragmentów kul - do objętości całej kuli o promieniu 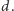 Co z fragmentami walców? Nietrudno zauważyć, że każdy z nich ma podstawę o powierzchni
Co z fragmentami walców? Nietrudno zauważyć, że każdy z nich ma podstawę o powierzchni 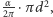 gdzie
gdzie 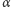 jest kątem zewnętrznym między ścianami spotykającymi się wzdłuż krawędzi będącej wysokością danego fragmentu walca. Jeśli więc przez
jest kątem zewnętrznym między ścianami spotykającymi się wzdłuż krawędzi będącej wysokością danego fragmentu walca. Jeśli więc przez 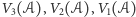 oznaczymy odpowiednio objętość
oznaczymy odpowiednio objętość 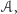 jego pole powierzchni oraz sumę długości krawędzi przemnożonych przez kąt zewnętrzny między odpowiednimi ścianami, otrzymamy
jego pole powierzchni oraz sumę długości krawędzi przemnożonych przez kąt zewnętrzny między odpowiednimi ścianami, otrzymamy
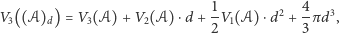 |
(*) |
gdzie 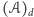 to obszar dostępny żyratoperzom o długości szyi wynoszącej
to obszar dostępny żyratoperzom o długości szyi wynoszącej 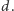 Oczywiście, jeśli wybieg żyratoperzy zostanie zmniejszony do wielościanu
Oczywiście, jeśli wybieg żyratoperzy zostanie zmniejszony do wielościanu 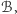 znajdującego się wewnątrz
znajdującego się wewnątrz 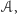 to obszar w zasięgu ich żarłocznych paszcz również ulegnie zmniejszeniu i w tej sytuacji
to obszar w zasięgu ich żarłocznych paszcz również ulegnie zmniejszeniu i w tej sytuacji
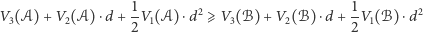 |
lub równoważnie
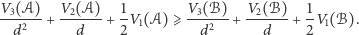 |
Widać, że wraz z wydłużaniem się żyratoperzych szyi rola składników związanych z objętościami i powierzchniami wielościanów w powyższym wzorze staje się zaniedbywalnie mała. W tej sytuacji otrzymujemy nierówność 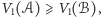 na której tak nam zależało.
na której tak nam zależało.
Wielkość 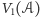 nosi nazwę 1-wymiarowej objętości wewnętrznej wielościanu
nosi nazwę 1-wymiarowej objętości wewnętrznej wielościanu 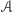 i dzięki wykazanej powyżej monotoniczności ze względu na zawieranie może być również określona dla dowolnego ciała wypukłego
i dzięki wykazanej powyżej monotoniczności ze względu na zawieranie może być również określona dla dowolnego ciała wypukłego 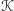 w przestrzeni poprzez przybliżanie ciała
w przestrzeni poprzez przybliżanie ciała 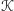 wielościanami w nim zawartymi. Posługując się tą definicją, trudno nam będzie jednak wyznaczyć tytułową "długość kuli", czyli
wielościanami w nim zawartymi. Posługując się tą definicją, trudno nam będzie jednak wyznaczyć tytułową "długość kuli", czyli 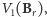 gdzie
gdzie 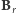 jest kulą o promieniu
jest kulą o promieniu 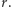 W sukurs przychodzi nam wzór (*), dziedziczony przez zbiory wypukłe po wielościanach, który po wykorzystaniu oczywistej zależności
W sukurs przychodzi nam wzór (*), dziedziczony przez zbiory wypukłe po wielościanach, który po wykorzystaniu oczywistej zależności 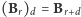 przyjmuje postać
przyjmuje postać
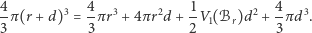 |
Równość ta po redukcji daje 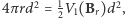 czyli
czyli 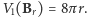 To więcej czy mniej od 1-wymiarowej objętości wewnętrznej sześcianu o tej samej, co kula, objętości?
To więcej czy mniej od 1-wymiarowej objętości wewnętrznej sześcianu o tej samej, co kula, objętości?
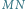 musi być tak krótki, by zmieścił się w czworościanie
musi być tak krótki, by zmieścił się w czworościanie 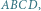 mimo, iż krawędzie
mimo, iż krawędzie 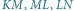 i
i 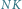 są tylko niewiele krótsze od krawędzi
są tylko niewiele krótsze od krawędzi 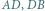 i
i