Mała Delta
Z żabami przez symetrię
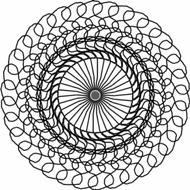
Chyba każdy patrzył kiedyś w kalejdoskop - prostokątne lustra odbijające różnobarwne wzory powstałe z przesypujących się koralików. Nie znam nikogo, kto mając w ręku owo urządzenie, byłby w stanie powstrzymać się przed choćby najmniejszym obróceniem nim i zerknięciem przez małe oczko na otrzymany efekt. A gdyby odwrócić sytuację i zbadać, jak zmieni się obraz, gdy zamiast koralikami poruszymy lustrami znajdującymi się w kalejdoskopie? Zacznijmy od wyprawy do szklarza i wyboru bohatera kalejdoskopowych przygód - po starannym castingu wygrywa żaba.
Lustrami będziemy manipulować w "kalejdoskopowy" sposób, czyli tak, żeby każde było prostopadłe do płaszczyzny wzoru. Gdy obok żaby zostanie umieszczone jedno lustro, powstaje oczywiście obraz dwóch żab. Dokładamy lustro drugie, umieszczając je prostopadle do pierwszego (i płaszczyzny obrazu), powstają cztery portrety. Uzyskany obraz ma dwie płaszczyzny symetrii oraz oś dwukrotną.
Zmniejszając kąt między lustrami, otrzymamy większą liczbę portretów, obrazy o różnych krotnościach osi (choć dla większości kątów obrazy nie będą miały osi symetrii). Co druga żaba patrzy w lewo, a pozostałe w prawo. Na zdjęciu poniżej widać oś "prawie" pięciokrotną (kąt między lustrami niedokładnie odpowiada 1/10 kąta pełnego). Manipulując kątem, można uzyskać właściwie dowolną krotność osi (zakładając, że obraz żaby może być dowolnie mały lub że lustra, którymi dysponujemy, są dowolnie duże).
Umieszczając lustra równolegle, obserwujemy nowy rodzaj przekształcenia - translację lub inaczej przesunięcie. Lustra (oraz ich odbicia) są płaszczyznami symetrii niekończącego się widoku żabich twarzy.

Czas na lustro trzecie. Utworzenie obrazu trójkąta równobocznego nie jest rzeczą łatwą. Problem stanowi grubość szyby oraz fakt, że warstwa srebra znajduje się za nią. Oczekiwane i faktyczne wyniki pracy przedstawione są na obrazkach poniżej.

Zmieńmy ustawienie tak, aby lustra tworzyły trójkąt o kątach 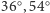 i
i 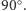 Nie zobaczymy śladu po symetrii translacyjnej. Uzyskany obraz pięciokąta foremnego stwarza nieregularności. To dlatego, że pięciokątami foremnymi nie można pokryć płaszczyzny. Takie pokrycie jest możliwe, między innymi, dla każdego trójkąta, kwadratu, prostokąta, równoległoboku i sześciokąta foremnego. Trzema lustrami można uzyskać regularne obrazy trójkątów równobocznych, kwadratów i sześciokątów (sprawdź, Czytelniku, dlaczego trzema lustrami nie można uzyskać regularnego obrazu prostokątów).
Nie zobaczymy śladu po symetrii translacyjnej. Uzyskany obraz pięciokąta foremnego stwarza nieregularności. To dlatego, że pięciokątami foremnymi nie można pokryć płaszczyzny. Takie pokrycie jest możliwe, między innymi, dla każdego trójkąta, kwadratu, prostokąta, równoległoboku i sześciokąta foremnego. Trzema lustrami można uzyskać regularne obrazy trójkątów równobocznych, kwadratów i sześciokątów (sprawdź, Czytelniku, dlaczego trzema lustrami nie można uzyskać regularnego obrazu prostokątów).

Rys. 1 Uzyskany obraz ma dwukrotną oś symetrii. Identyczny obraz żab uzyskamy, obracając go o kąt 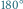 i
i 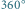

Rys. 2 Obraz mający 34-krotną oś symetrii
Obraz nazywamy symetrycznym, gdy nie potrafimy odróżnić, czy został on poddany przekształceniu (translacji, obrotowi, odbiciu lub paru z nich) czy też nie. Zbiór wszystkich przekształceń danego obiektu, które odwzorowują go na siebie, nazywamy grupą symetrii. Grupą symetrii pokazanego na marginesie obrazu czterech żab (Rys. 1) jest 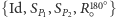 (obrót o kąt
(obrót o kąt 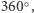 dwie płaszczyzny symetrii, obrót o kąt
dwie płaszczyzny symetrii, obrót o kąt 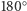 ), a znajdującej się pod nim serwetki
), a znajdującej się pod nim serwetki 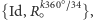 gdzie
gdzie 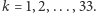 W przypadku obrazu żab wszystkie elementy symetrii przecinają się w jednym punkcie, taką grupę nazywamy punktową. Istnieje dokładnie jeden punkt, który nie zmienia swojego położenia przy poddaniu obiektu dowolnemu przekształceniu z grupy.
W przypadku obrazu żab wszystkie elementy symetrii przecinają się w jednym punkcie, taką grupę nazywamy punktową. Istnieje dokładnie jeden punkt, który nie zmienia swojego położenia przy poddaniu obiektu dowolnemu przekształceniu z grupy.
Symetria translacyjna nie występuje w grupach punktowych, bo powoduje przesunięcie równoległe wszystkich punktów danego obiektu. Translacja może być elementem grupy symetrii tylko figury nieograniczonej, to znaczy niezerowe przesunięcie tylko figury nieograniczonej może spowodować, że będzie ona nierozróżnialna z obrazem nieprzesuniętym. Patrząc na wytapetowaną (nieograniczoną) ścianę poza oczywistą translacją, można zauważyć również inne elementy symetrii. Najmniejszy element wzoru, który powielany i przesuwany (tylko translacja, żadne inne przekształcenie) w różne strony tworzy całość, nazywamy komórką elementarną. Komórka elementarna sama w sobie może mieć własności symetryczne. Najmniejszy element wzoru, który poddany przekształceniom symetrycznym tworzy komórkę elementarną nazywamy motywem.
Nie wszystkie elementy symetrii mogą łączyć się ze sobą. Na przykład symetria translacyjna może współistnieć tylko z osiami o krotności 2, 3, 4, i 6. Powoduje to ograniczenie liczby rodzajów tapet (mających różne grupy symetrii) - na płaszczyźnie występuje ich 17.
Poniżej przedstawiono 6 tapet, których grupy symetrii są różne. Na każdym obrazku kolorem szarym zaznaczono komórkę elementarną. Do grupy symetrii tapety w lewym górnym rogu poza 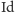 (obrotem o
(obrotem o 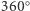 ) należy tylko translacja, nie obserwujemy żadnej innej symetrii. Na tapecie w prawym górnym rogu poza translacją pojawia się również płaszczyzna symetrii w komórce elementarnej. Zachęcamy Czytelnika do samodzielnego znalezienia pozostałych jedenastu tapet o innych grupach symetrii niż poniższe.
) należy tylko translacja, nie obserwujemy żadnej innej symetrii. Na tapecie w prawym górnym rogu poza translacją pojawia się również płaszczyzna symetrii w komórce elementarnej. Zachęcamy Czytelnika do samodzielnego znalezienia pozostałych jedenastu tapet o innych grupach symetrii niż poniższe.

Powyższe tapety zostały wygenerowane programem Escher2D, którym w prosty sposób można tworzyć własne wzory w każdej z 17 grup symetrii. Program umożliwia również tworzenie obrazów o dowolnej krotności osi symetrii - no, może prawie dowolnej, bo największa możliwa krotność to 1000. Możliwości stworzenia swojego, w jakiś sposób symetrycznego wzoru jest mnóstwo, a frajdy przy tworzeniu "tapety" tak samo dużo, jak przy obracaniu kalejdoskopem.
Symetria występuje również w przestrzeni trójwymiarowej, ale to temat na inną historię...
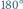 i
i 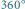
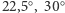 albo
albo 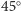 ) lub trzy, tworzące ściany graniastosłupa prawidłowego trójkątnego.
) lub trzy, tworzące ściany graniastosłupa prawidłowego trójkątnego.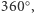 zawsze wrócimy do sytuacji początkowej. Może jednak istnieć taka prosta, że w trakcie obracania obrazu dookoła niej o kąt pełny parokrotnie otrzymamy rezultat nierozróżnialny z początkowym. Wtedy mówimy o wielokrotnej osi symetrii.
zawsze wrócimy do sytuacji początkowej. Może jednak istnieć taka prosta, że w trakcie obracania obrazu dookoła niej o kąt pełny parokrotnie otrzymamy rezultat nierozróżnialny z początkowym. Wtedy mówimy o wielokrotnej osi symetrii.