Czy Ziemia jest płaska?
Pozwolę sobie podtrzymać Czytelnika w napięciu i tytułowe pytanie tymczasem zostawię bez odpowiedzi. Zacznę za to od refleksji, czym jest płaskość.
Każdy rozsądny człowiek za prototyp płaskiej powierzchni uzna fragment płaszczyzny, na przykład w postaci kartki papieru leżącej na stole. A jeśli taką kartkę wygiąć w kształt walca, czy nadal jest ona płaska? Tutaj zdania mogą być podzielone. Większość z nas uzna, że nie, i całkiem słusznie, bo takie znaczenie ma w codziennym języku słowo płaski.
Warto jednak zauważyć, że w myśl takiej definicji świat powierzchni płaskich jest bardzo ubogi - ogranicza się do jednej jedynej płaszczyzny.
W matematyce funkcjonuje alternatywna definicja, która opiera się wyłącznie na wewnętrznych własnościach danej powierzchni, a nie na tym, jak ową powierzchnię ułożymy w przestrzeni czy wygniemy. Przez geometrię wewnętrzną powierzchni rozumiemy ogół takich własności - wszystkie wyniki pomiarów długości krzywych leżących na tej powierzchni. Dwie powierzchnie nazwiemy izometrycznymi, jeśli istnieje między nimi izometria, to jest ciągłe przekształcenie zachowujące wszystkie powyższe wielkości. Ostatecznie, powierzchnię uznamy za płaską, jeśli da się ją podzielić na fragmenty, z których każdy jest izometryczny z fragmentem płaszczyzny.
Przejdźmy do przykładów. Pierwszym przykładem izometrii jest właśnie wspomniane wcześniej wygięcie kartki. Istotnie, dowolna krzywa narysowana na kartce po wygięciu ma tę samą długość, co i przedtem. Widzimy więc, że w myśl naszej definicji zgięta kartka jest izometryczna z wyprostowaną, w szczególności nadal jest płaska.

Rys. 1
Podobnie jest z powierzchnią boczną walca. Nie jest ona co prawda izometryczna z fragmentem płaszczyzny (dlaczego?), składa się jednak z dwóch fragmentów, z których każdy daje się wyprostować (rysunek 1). W związku z tym powierzchnia boczna walca jest płaska, podobnie sprawa ma się też z powierzchnią boczną stożka.
Spróbujmy teraz odpowiedzieć na pytanie zadane w tytule. Dla uproszczenia przyjmijmy, że powierzchnia Ziemi ma kształt sfery i zapytajmy: czy sfera jest płaska? Zauważmy, że problem jest istotnie trudniejszy niż dotychczasowe rozważania - by wykazać, że powierzchnia jest płaska, wystarczy wskazać odpowiednie przekształcenie lub przekształcenia. Jeśli natomiast chcemy zaprzeczyć płaskości, musimy się upewnić, że żadne takie przekształcenie nie istnieje. W tym celu zazwyczaj wprowadza się niezmienniki. W naszym przypadku będzie to... wzór na długość okręgu.
Aby wyznaczyć taki wzór, możemy posługiwać się wyłącznie pojęciami geometrii wewnętrznej. Na początek zauważmy, że możemy określić odległość między dwoma punktami 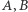 powierzchni
powierzchni 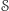 jako kres dolny (w rozważanych tu przypadkach zawsze będzie to minimum) długości krzywych o początku w
jako kres dolny (w rozważanych tu przypadkach zawsze będzie to minimum) długości krzywych o początku w 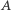 i końcu w
i końcu w 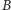 zawartych w
zawartych w 
Dla płaszczyzny takie minimum jest osiągane dla odcinka 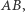 więc zdefiniowana właśnie odległość pokrywa się ze standardową. Natomiast na sferze krzywą o minimalnej długości jest łuk
więc zdefiniowana właśnie odległość pokrywa się ze standardową. Natomiast na sferze krzywą o minimalnej długości jest łuk 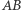 okręgu wielkiego (czyli okręgu otrzymanego jako przekrój sfery płaszczyzną przechodzącą przez jej środek). Przykładowo na sferze o promieniu
okręgu wielkiego (czyli okręgu otrzymanego jako przekrój sfery płaszczyzną przechodzącą przez jej środek). Przykładowo na sferze o promieniu 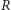 odległość między dwoma punktami antypodycznymi jest długością połowy równika, a więc wynosi
odległość między dwoma punktami antypodycznymi jest długością połowy równika, a więc wynosi 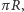 podczas gdy standardowa odległość w przestrzeni to
podczas gdy standardowa odległość w przestrzeni to 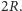
Nie będzie zaskoczeniem, jeśli okrąg o środku 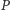 i promieniu
i promieniu  (oznaczany jako
(oznaczany jako 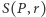 ) zdefiniujemy jako zbiór wszystkich punktów powierzchni odległych od punktu
) zdefiniujemy jako zbiór wszystkich punktów powierzchni odległych od punktu 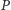 o
o 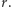 Przez
Przez 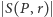 oznaczymy długość tej krzywej. Oczywiście, na płaszczyźnie długość ta wyraża się wzorem
oznaczymy długość tej krzywej. Oczywiście, na płaszczyźnie długość ta wyraża się wzorem 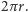 A jak jest na sferze o promieniu
A jak jest na sferze o promieniu 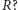 Zauważmy, że dowolny okrąg o promieniu większym od
Zauważmy, że dowolny okrąg o promieniu większym od 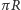 okazuje się zbiorem pustym, nie ma więc co mówić o jego długości. Natomiast okrąg o promieniu
okazuje się zbiorem pustym, nie ma więc co mówić o jego długości. Natomiast okrąg o promieniu 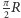 jest okręgiem wielkim, toteż ma długość
jest okręgiem wielkim, toteż ma długość 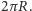 Widzimy w szczególności, że zdefiniowane właśnie okręgi na sferze są w przestrzeni jednocześnie okręgami w zwyczajnym sensie - dla uniknięcia nieporozumień w drugim przypadku będziemy mówić o okręgu euklidesowym, z euklidesowym środkiem i promieniem.
Widzimy w szczególności, że zdefiniowane właśnie okręgi na sferze są w przestrzeni jednocześnie okręgami w zwyczajnym sensie - dla uniknięcia nieporozumień w drugim przypadku będziemy mówić o okręgu euklidesowym, z euklidesowym środkiem i promieniem.
Rys. 2
Rys. 3
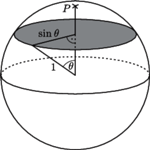
Dla ustalenia uwagi za punkt 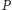 przyjmijmy biegun północny sfery i ustalmy promień sfery równy
przyjmijmy biegun północny sfery i ustalmy promień sfery równy 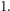 Wówczas okrąg
Wówczas okrąg 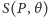 jest równoleżnikiem odpowiadającym szerokości geograficznej
jest równoleżnikiem odpowiadającym szerokości geograficznej 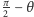 (kąty mierzymy tu w radianach). Jak pokazuje rysunek 2, ma on euklidesowy promień równy
(kąty mierzymy tu w radianach). Jak pokazuje rysunek 2, ma on euklidesowy promień równy 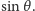 W ten sposób otrzymujemy wzór na długość okręgu
W ten sposób otrzymujemy wzór na długość okręgu

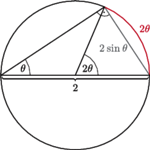
Wiemy, że na płaszczyźnie byłoby to 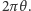 Porównanie długości łuku i cięciwy na rysunku 3 pokazuje, że
Porównanie długości łuku i cięciwy na rysunku 3 pokazuje, że 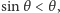 a więc okręgi na sferze są krótsze od ich odpowiedników na płaszczyźnie. Gdyby pewne otoczenie punktu
a więc okręgi na sferze są krótsze od ich odpowiedników na płaszczyźnie. Gdyby pewne otoczenie punktu  na sferze było izometryczne z fragmentem płaszczyzny, to te dwa wzory musiałyby się pokrywać, przynajmniej dla odpowiednio małych wartości
na sferze było izometryczne z fragmentem płaszczyzny, to te dwa wzory musiałyby się pokrywać, przynajmniej dla odpowiednio małych wartości 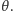
W ten sposób możemy z ulgą skonstatować, że Ziemia nie jest płaska.