Odbicia w dwóch zwierciadłach

Odbicie światła od zwierciadła płaskiego, przerabiane w szkole w ramach optyki geometrycznej, uważane jest za zagadnienie banalne. Bywa czasem uatrakcyjniane rozważaniem kwestii, dlaczego lustro zamienia stronę lewą z prawą, a nie zamienia góry z dołem. Natomiast znacznie ciekawsze - a architektom niezwykle przydatne w projektowaniu ciekawych wnętrz - okazuje się zbadanie zjawiska odbicia światła od pary zwierciadeł, których płaszczyzny tworzą dowolny kąt. Może wtedy dojść do wielokrotnych odbić, w wyniku których powstaje wiele obrazów. Okazuje się, że liczba powstałych obrazów zależy nie tylko od kąta między zwierciadłami, ale też od położenia przedmiotu.
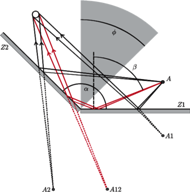
Rys. 1 Schemat zjawiska wielokrotnego odbicia dla kąta między zwierciadłami równego 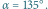

Fot. 1 Kąt między zwierciadłami jest równy 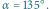 Kredka leżąca w obszarze zacieniowanego klina ma dwa obrazy, kredka położona poza klinem - trzy.
Kredka leżąca w obszarze zacieniowanego klina ma dwa obrazy, kredka położona poza klinem - trzy.
Rozważmy więc dwa zwierciadła stykające się wzdłuż pewnej krawędzi, przed którymi znajduje się oglądany przedmiot, który dla wygody utożsamimy z pojedynczym punktem. Oznaczmy przez 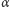 kąt, jaki tworzą odbijające płaszczyzny zwierciadeł. Możemy przyjąć, że zachodzi
kąt, jaki tworzą odbijające płaszczyzny zwierciadeł. Możemy przyjąć, że zachodzi 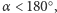 gdyż dla kątów większych od
gdyż dla kątów większych od 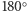 odbicia wielokrotne nie mogą wystąpić, a dla
odbicia wielokrotne nie mogą wystąpić, a dla 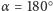 mamy po prostu do czynienia z jednym zwierciadłem. Z najprostszym przypadkiem mamy do czynienia dla
mamy po prostu do czynienia z jednym zwierciadłem. Z najprostszym przypadkiem mamy do czynienia dla 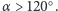 Promienie wychodzące z przedmiotu ulegają wtedy najmniejszej ilości odbić. Jako przykład wybierzmy
Promienie wychodzące z przedmiotu ulegają wtedy najmniejszej ilości odbić. Jako przykład wybierzmy 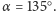 Rysunek 1 pokazuje, jak zwierciadło
Rysunek 1 pokazuje, jak zwierciadło 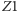 wytwarza obraz
wytwarza obraz 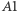 przedmiotu
przedmiotu 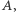 a zwierciadło
a zwierciadło 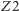 - obraz
- obraz 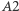 ; powstają więc dwa obrazy. Promienie odbite trafiają do oka obserwatora (oznaczonego kółkiem) z dwóch kierunków.
; powstają więc dwa obrazy. Promienie odbite trafiają do oka obserwatora (oznaczonego kółkiem) z dwóch kierunków.
Możliwe jest powstanie trzeciego obrazu widocznego dla tego samego obserwatora, gdy promienie padające z punktu 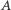 odbijają się kolejno od zwierciadeł
odbijają się kolejno od zwierciadeł 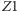 i
i 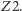 Punkt przecięcia przedłużeń promieni wychodzących z układu wyznacza położenie obrazu
Punkt przecięcia przedłużeń promieni wychodzących z układu wyznacza położenie obrazu 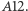 Jest to możliwe, jeśli kąt odbicia od pierwszego zwierciadła
Jest to możliwe, jeśli kąt odbicia od pierwszego zwierciadła 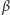 (a więc i kąt padania na nie) jest większy od
(a więc i kąt padania na nie) jest większy od 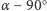 (
( 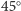 w naszym przykładzie), bo tylko wtedy promień odbity od
w naszym przykładzie), bo tylko wtedy promień odbity od 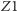 trafia na zwierciadło
trafia na zwierciadło 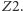 Wynika stąd, że trzy obrazy powstają, jeśli punkt przedmiotu należy do obszaru przylegającego do zwierciadła
Wynika stąd, że trzy obrazy powstają, jeśli punkt przedmiotu należy do obszaru przylegającego do zwierciadła 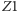 i ograniczonego płaszczyzną tworzącą z nim kąt
i ograniczonego płaszczyzną tworzącą z nim kąt 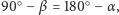 czyli
czyli 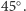 Zauważmy, że podwójnemu odbiciu ulegają tylko promienie zmierzające ku zwierciadłu
Zauważmy, że podwójnemu odbiciu ulegają tylko promienie zmierzające ku zwierciadłu 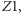 natomiast promienie wychodzące z tego obszaru w kierunku zwierciadła
natomiast promienie wychodzące z tego obszaru w kierunku zwierciadła 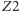 odbijają się tylko raz. Oczywiście, istnieje drugi obszar o takich samych właściwościach przyległy do
odbijają się tylko raz. Oczywiście, istnieje drugi obszar o takich samych właściwościach przyległy do 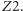 Promienie wychodzące z niego ulegają podwójnemu odbiciu, jeśli biegną ku zwierciadłu
Promienie wychodzące z niego ulegają podwójnemu odbiciu, jeśli biegną ku zwierciadłu 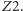 Widać więc, że promienie pochodzące z każdego z tych dwóch obszarów mogą wytworzyć trzy obrazy: dwa powstałe z pojedynczych odbić od każdego lustra i jeden powstały w wyniku dwukrotnego odbicia. Jeśli natomiast przedmiot znajduje się pomiędzy wyróżnionymi płaszczyznami, czyli należy do obszaru w kształcie klina określonego kątem
Widać więc, że promienie pochodzące z każdego z tych dwóch obszarów mogą wytworzyć trzy obrazy: dwa powstałe z pojedynczych odbić od każdego lustra i jeden powstały w wyniku dwukrotnego odbicia. Jeśli natomiast przedmiot znajduje się pomiędzy wyróżnionymi płaszczyznami, czyli należy do obszaru w kształcie klina określonego kątem 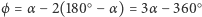 (tu:
(tu: 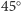 ), to możliwe są tylko dwa pojedyncze odbicia. Z ostatniego wzoru wynika, że dla
), to możliwe są tylko dwa pojedyncze odbicia. Z ostatniego wzoru wynika, że dla 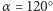 kąt
kąt 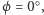 a więc klin zastąpiony jest płaszczyzną dzielącą obszar między lustrami na połowy. Punkt przedmiotu dowolnie położony poza tą płaszczyzną ma trzy obrazy.
a więc klin zastąpiony jest płaszczyzną dzielącą obszar między lustrami na połowy. Punkt przedmiotu dowolnie położony poza tą płaszczyzną ma trzy obrazy.
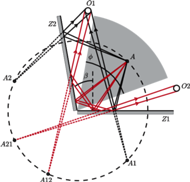
Rys. 2 Schemat zjawiska wielokrotnego odbicia dla kąta między zwierciadłami równego 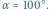

Fot. 2 Kąt między zwierciadłami jest równy 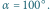 Widać po trzy obrazy każdej z kredek. Kredka położona w obszarze zacieniowanego klina może mieć jeszcze jeden obraz, ale jest on niewidoczny z wybranego miejsca obserwacji.
Widać po trzy obrazy każdej z kredek. Kredka położona w obszarze zacieniowanego klina może mieć jeszcze jeden obraz, ale jest on niewidoczny z wybranego miejsca obserwacji.
Jeśli kąt 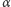 jest mniejszy od
jest mniejszy od 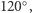 lecz nadal jest rozwarty, to również można wyróżnić takie obszary między lustrami, że promienie z nich wychodzące ulegają różnej ilości odbić. Rysunek 2 ilustruje to dla
lecz nadal jest rozwarty, to również można wyróżnić takie obszary między lustrami, że promienie z nich wychodzące ulegają różnej ilości odbić. Rysunek 2 ilustruje to dla 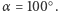 Podobnie jak poprzednio promień wychodzący z wybranego punktu odbija się dwa razy, jeśli pierwszy kąt odbicia spełnia warunek
Podobnie jak poprzednio promień wychodzący z wybranego punktu odbija się dwa razy, jeśli pierwszy kąt odbicia spełnia warunek 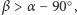 czyli
czyli 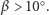 Płaszczyzna ograniczająca zbiór takich punktów przylegający do zwierciadła
Płaszczyzna ograniczająca zbiór takich punktów przylegający do zwierciadła 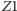 tworzy z tym zwierciadłem kąt
tworzy z tym zwierciadłem kąt 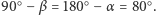 Punkty przedmiotu należące do tego obszaru mają więc trzy obrazy, tak jak w poprzednim przykładzie. Drugi obszar, utworzony przez punkty o tej samej własności, przylega do zwierciadła
Punkty przedmiotu należące do tego obszaru mają więc trzy obrazy, tak jak w poprzednim przykładzie. Drugi obszar, utworzony przez punkty o tej samej własności, przylega do zwierciadła 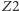 i ma wielkość określoną takim samym kątem. Oba obszary pokrywają się częściowo. Część wspólna tworzy klin o rozwartości
i ma wielkość określoną takim samym kątem. Oba obszary pokrywają się częściowo. Część wspólna tworzy klin o rozwartości 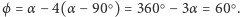 Każdy punkt tego klina ma cztery obrazy: dwa powstałe po pojedynczych odbiciach i dwa utworzone w wyniku podwójnych odbić w obu zwierciadłach. Rysunek 2 ilustruje także fakt, że nie wszystkie obrazy są widoczne z jednego miejsca: obserwator
Każdy punkt tego klina ma cztery obrazy: dwa powstałe po pojedynczych odbiciach i dwa utworzone w wyniku podwójnych odbić w obu zwierciadłach. Rysunek 2 ilustruje także fakt, że nie wszystkie obrazy są widoczne z jednego miejsca: obserwator 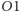 nie może zobaczyć obrazu
nie może zobaczyć obrazu 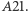 Klin powiększa się, gdy
Klin powiększa się, gdy 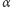 maleje, i przy
maleje, i przy 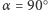 zajmuje cały obszar między zwierciadłami, tj.
zajmuje cały obszar między zwierciadłami, tj. 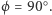 Jednak przy tym szczególnym kącie oba obrazy uzyskane przez podwójne odbicia dokładnie się pokrywają, tzn.
Jednak przy tym szczególnym kącie oba obrazy uzyskane przez podwójne odbicia dokładnie się pokrywają, tzn. 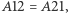 więc każdy punkt przedmiotu ma tylko trzy obrazy.
więc każdy punkt przedmiotu ma tylko trzy obrazy.

Rys. 3 Schemat zjawiska wielokrotnego odbicia dla kąta między zwierciadłami równego 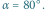

Fot. 4 Liczba obrazów która powstaje przy danym kącie 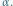 Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.
Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.
Gdy kąt między lustrami jest mniejszy od 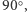 to podwójne odbicie od każdego zwierciadła zachodzi dla każdego punktu położonego między zwierciadłami. Powstają więc zawsze co najmniej cztery obrazy. Ponadto pojawia się możliwość trzykrotnego odbicia zilustrowana dalej na rysunku 3 dla
to podwójne odbicie od każdego zwierciadła zachodzi dla każdego punktu położonego między zwierciadłami. Powstają więc zawsze co najmniej cztery obrazy. Ponadto pojawia się możliwość trzykrotnego odbicia zilustrowana dalej na rysunku 3 dla 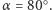 Trzecie odbicie, wytwarzające obraz
Trzecie odbicie, wytwarzające obraz 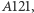 jest możliwe, jeśli promień z punktu przedmiotu pada np. na zwierciadło
jest możliwe, jeśli promień z punktu przedmiotu pada np. na zwierciadło 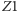 pod kątem
pod kątem 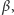 odbija się, dociera do
odbija się, dociera do 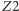 i po drugim odbiciu skierowany jest ku zwierciadłu
i po drugim odbiciu skierowany jest ku zwierciadłu 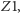 tj. pada na nie pod kątem
tj. pada na nie pod kątem 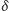 mniejszym od
mniejszym od 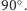 Wspomagając się rysunkiem 3, można wykazać, że kąty
Wspomagając się rysunkiem 3, można wykazać, że kąty 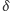 i
i 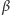 są powiązane relacją
są powiązane relacją 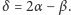 W granicznym przypadku
W granicznym przypadku 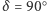 relacja ta określa kąt
relacja ta określa kąt 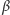 (w naszym przykładzie równy
(w naszym przykładzie równy 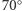 ), który wyznacza szerokość kątową
), który wyznacza szerokość kątową 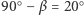 obszaru przyległego do zwierciadła
obszaru przyległego do zwierciadła 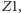 złożonego z punktów wysyłających promienie odbijające się trzykrotnie. Drugi taki obszar przylega do zwierciadła
złożonego z punktów wysyłających promienie odbijające się trzykrotnie. Drugi taki obszar przylega do zwierciadła 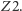 Pomiędzy tymi obszarami utworzony jest klin o rozwartości
Pomiędzy tymi obszarami utworzony jest klin o rozwartości 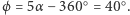 Punkty mieszczące się w klinie mają po cztery obrazy, a te na zewnątrz klina - po pięć. Klin zmniejsza się, gdy
Punkty mieszczące się w klinie mają po cztery obrazy, a te na zewnątrz klina - po pięć. Klin zmniejsza się, gdy 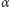 maleje i redukuje się do płaszczyzny dwusiecznej dla
maleje i redukuje się do płaszczyzny dwusiecznej dla 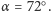
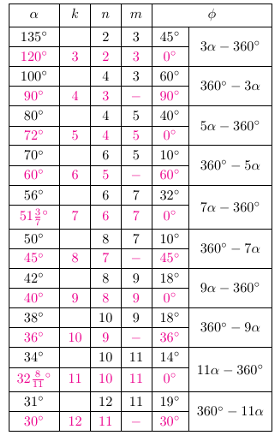
Analogiczne rozważania kontynuowane dla coraz mniejszych kątów 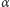 dają podobne wyniki, pokazując podział przestrzeni między lustrami na obszary, którym odpowiadają różne liczby obrazów. Ogólnie liczba obrazów rośnie, gdy
dają podobne wyniki, pokazując podział przestrzeni między lustrami na obszary, którym odpowiadają różne liczby obrazów. Ogólnie liczba obrazów rośnie, gdy 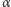 maleje, i zmierza do nieskończoności, gdy zwierciadła stają się równoległe. Wszystkie one, jak również obserwowany przedmiot, leżą na okręgu o środku położonym na wspólnej krawędzi zwierciadeł.
maleje, i zmierza do nieskończoności, gdy zwierciadła stają się równoległe. Wszystkie one, jak również obserwowany przedmiot, leżą na okręgu o środku położonym na wspólnej krawędzi zwierciadeł.
Wyróżniają się kąty, których pewne wielokrotności stanowią kąt pełny, tj. 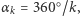 gdzie
gdzie 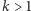 jest liczbą naturalną. Liczba
jest liczbą naturalną. Liczba  obrazów powstających dla tych kątów dana jest wzorem
obrazów powstających dla tych kątów dana jest wzorem 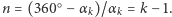 Wzór ten jest słuszny tylko dla punktów mieszczących się w obszarach w kształcie klina lub na płaszczyźnie dwusiecznej, do której kurczy się on dla pewnych kątów
Wzór ten jest słuszny tylko dla punktów mieszczących się w obszarach w kształcie klina lub na płaszczyźnie dwusiecznej, do której kurczy się on dla pewnych kątów 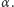 Tabela zawiera także wartości
Tabela zawiera także wartości 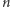 dla przykładowych kątów wybranych z przedziałów zawartych między wartościami
dla przykładowych kątów wybranych z przedziałów zawartych między wartościami 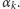 Liczba
Liczba 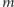 oznacza liczbę obrazów punktów znajdujących się poza klinem.
oznacza liczbę obrazów punktów znajdujących się poza klinem.
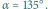
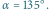 Kredka leżąca w obszarze zacieniowanego klina ma dwa obrazy, kredka położona poza klinem - trzy.
Kredka leżąca w obszarze zacieniowanego klina ma dwa obrazy, kredka położona poza klinem - trzy.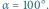
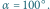 Widać po trzy obrazy każdej z kredek. Kredka położona w obszarze zacieniowanego klina może mieć jeszcze jeden obraz, ale jest on niewidoczny z wybranego miejsca obserwacji.
Widać po trzy obrazy każdej z kredek. Kredka położona w obszarze zacieniowanego klina może mieć jeszcze jeden obraz, ale jest on niewidoczny z wybranego miejsca obserwacji.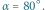
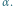 Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.
Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.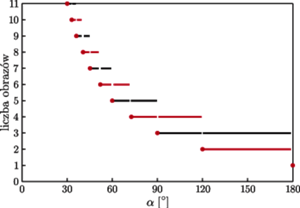
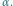 Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.
Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.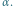 Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.
Kolorowe linie i punkty dotyczą przedmiotów położonych w obrębie klina, a czarne linie - poza klinem.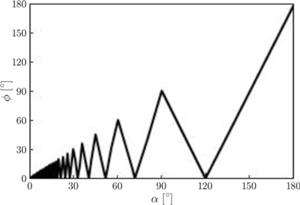
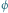 w zależności od kąta między lustrami.
w zależności od kąta między lustrami. w zależności od kąta między lustrami.
w zależności od kąta między lustrami.