Drobiazgi
Mała Delta
Nawijamy, odwijamy
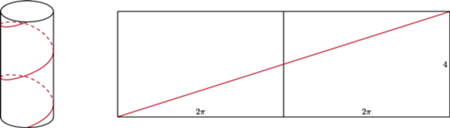
Jaką długość ma linia śrubowa owijająca dwukrotnie walec o promieniu 1 i wysokości 4, tak jak widać na obrazku? Oczywiście, 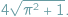 Aby przekonać się, że rzeczywiście, wystarczy spojrzeć na obrazek z prawej - jeśli nawiniemy go na walec, to otrzymamy obrazek z lewej.
Aby przekonać się, że rzeczywiście, wystarczy spojrzeć na obrazek z prawej - jeśli nawiniemy go na walec, to otrzymamy obrazek z lewej.
To elementarne, Watsonie!
Wobec tego zapytajmy teraz o to, jaką długość ma jeden okres sinusoidy (czyli od jakiegoś kąta 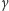 do kąta
do kąta 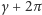 ), bo tego nie ma w poradnikach.
), bo tego nie ma w poradnikach.
Oczywiście, nie podamy konkretnej liczby, tylko wskażemy inną linię tej samej długości - jest nią elipsa o osiach długości 2 i 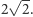 W tym celu wystarczy zauważyć, że jeśli walec o promieniu 1 (ten sam co poprzednio!) owiniemy papierem, a następnie przetniemy płaszczyzną tworzącą z jego osią kąt
W tym celu wystarczy zauważyć, że jeśli walec o promieniu 1 (ten sam co poprzednio!) owiniemy papierem, a następnie przetniemy płaszczyzną tworzącą z jego osią kąt 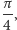 to obie otrzymane części papieru po rozwinięciu będą miały jeden z brzegów dokładnie sinusoidalny. To też nietrudno obliczyć. A przecięcie walca płaszczyzną to elipsa (czasami będąca okręgiem). Możemy nawet obliczyć, co otrzymamy przy dowolnym przecięciu owiniętego walca płaszczyzną. Przyjmijmy oznaczenia z rysunku na marginesie. Niech
to obie otrzymane części papieru po rozwinięciu będą miały jeden z brzegów dokładnie sinusoidalny. To też nietrudno obliczyć. A przecięcie walca płaszczyzną to elipsa (czasami będąca okręgiem). Możemy nawet obliczyć, co otrzymamy przy dowolnym przecięciu owiniętego walca płaszczyzną. Przyjmijmy oznaczenia z rysunku na marginesie. Niech 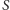 będzie środkiem koła dzielącego na pół elipsę otrzymaną z przecięcia walca płaszczyzną tworzącą z osią walca kąt
będzie środkiem koła dzielącego na pół elipsę otrzymaną z przecięcia walca płaszczyzną tworzącą z osią walca kąt 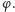 Ograniczający to koło okrąg przetnie elipsę w dwóch punktach będących końcami jego średnicy - jeden z nich oznaczmy przez
Ograniczający to koło okrąg przetnie elipsę w dwóch punktach będących końcami jego średnicy - jeden z nich oznaczmy przez 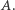

Płaszczyzna elipsy i płaszczyzna koła tworzą kąt dwuścienny o rozwartości 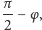 czyli gdy poprowadzimy z dowolnego punktu prostej
czyli gdy poprowadzimy z dowolnego punktu prostej 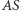 proste do niej prostopadłe w obu tych płaszczyznach, taki też będzie kąt między nimi.
proste do niej prostopadłe w obu tych płaszczyznach, taki też będzie kąt między nimi.
Niech teraz 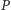 będzie dowolnym punktem elipsy. Zrzutujmy go prostopadle na okrąg, otrzymując punkt
będzie dowolnym punktem elipsy. Zrzutujmy go prostopadle na okrąg, otrzymując punkt 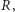 który z kolei zrzutujemy prostopadle na
który z kolei zrzutujemy prostopadle na 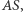 otrzymując punkt
otrzymując punkt 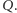
Mamy zatem 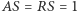 i
i 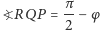 ; oznaczmy też
; oznaczmy też 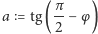 oraz
oraz 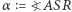 - jest to zarazem długość łuku (po rozwinięciu papieru - odcinka)
- jest to zarazem długość łuku (po rozwinięciu papieru - odcinka) 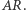
Bez trudu zauważamy, że 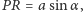 co oznacza, że po rozwinięciu przeciętego papieru otrzymamy wykres sinusa, którego wartości zostały pomnożone przez
co oznacza, że po rozwinięciu przeciętego papieru otrzymamy wykres sinusa, którego wartości zostały pomnożone przez 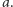 Oryginalną sinusoidę otrzymamy dla
Oryginalną sinusoidę otrzymamy dla 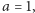 czyli gdy
czyli gdy 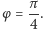
Dla 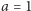 i
i 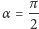 odcinek
odcinek 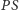 (czyli dłuższa półoś elipsy) będzie miał długość
(czyli dłuższa półoś elipsy) będzie miał długość 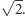 Krótszą osią elipsy będzie średnica okręgu.
Krótszą osią elipsy będzie średnica okręgu.
Prawda, że nie bolało?