Deltoid
Desargues i nożyce
W geometrii rzutowej przyjmujemy, że każde dwie proste równoległe przecinają się w pewnym ustalonym punkcie w nieskończoności, odpowiadającym ich kierunkowi, oraz że wszystkie takie punkty w nieskończoności tworzą prostą ("horyzont"). Poniżej przedstawiamy przykłady pojęć i twierdzeń rzutowych oraz ich zastosowań; dopuszczamy w nich takie właśnie punkty przecięcia "na horyzoncie".

Rys. 1
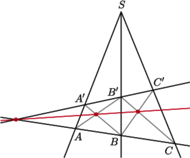
Rys. 2
Dane są trójkąty 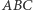 oraz
oraz 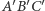 (Rys. 1). Jeśli proste
(Rys. 1). Jeśli proste 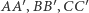 przecinają się w jednym punkcie
przecinają się w jednym punkcie 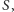 to punkt ten nazywamy środkiem perspektywicznym danych trójkątów. Jeśli punkty
to punkt ten nazywamy środkiem perspektywicznym danych trójkątów. Jeśli punkty 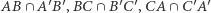 leżą na jednej prostej
leżą na jednej prostej 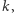 to nazywamy ją osią perspektywiczną danych trójkątów.
to nazywamy ją osią perspektywiczną danych trójkątów.
Twierdzenie (Desarguesa). Dwa trójkąty mają środek perspektywiczny wtedy i tylko wtedy, gdy mają oś perspektywiczną.
Każda taka płaska konfiguracja jest rzutem pewnej konfiguracji trójwymiarowej, można więc dowodzić tego twierdzenia przestrzennie (dowód w jedną stronę opisano w deltoidzie 5/2010).
Twierdzenie (O nożycach.). Pęk prostych o wierzchołku 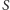 przecięto dwiema prostymi, po czym narysowano przekątne uzyskanych w ten sposób czworokątów, jak na rysunku 2. Wówczas kolorowe punkty są współliniowe.
przecięto dwiema prostymi, po czym narysowano przekątne uzyskanych w ten sposób czworokątów, jak na rysunku 2. Wówczas kolorowe punkty są współliniowe.
Dowód. Trójkąty 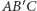 i
i 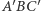 mają środek perspektywiczny
mają środek perspektywiczny 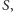 więc z twierdzenia Desarguesa mają też oś perspektywiczną, co kończy dowód dla pęku trzech prostych. Gdy jest ich więcej, wystarczy rozważać kolejne trójki spośród nich.
więc z twierdzenia Desarguesa mają też oś perspektywiczną, co kończy dowód dla pęku trzech prostych. Gdy jest ich więcej, wystarczy rozważać kolejne trójki spośród nich.