Dowód w stylu greckim
Rozpowszechnione jest przeświadczenie, że znaczna część dowodów geometrycznych prowadzonych przez mędrców Złotego Wieku Grecji, a więc czasów po zwycięskich wojnach perskich i kojarzących się nam np. z Peryklesem, wyglądała tak, iż był to rysunek ze słownym komentarzem: Patrz. Niezależnie od podziwu dla intelektualnej estetyki takich dowodów podejrzewamy, że dotyczyły one problemów mało skomplikowanych, rozumowań wymagających jednego kroku myślowego.
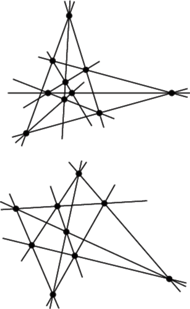
Rys. 1 Przykładowe konfiguracje Desarguesa i Pascala.
Tutaj chciałem przedstawić taki "grecki" dowód twierdzenia, które zostało odkryte dopiero po 250 latach od postawienia problemu.
Zapewne część z Czytelników pamięta problem posadzenia dziesięciu drzew w dziesięciu rzędach po trzy w każdym rzędzie i dziewięciu drzew w dziewięciu rzędach po trzy w każdym rzędzie. Przykładowe rozwiązania (a jest ich wiele) przedstawia rysunek 1. Problemy te zajmują poczesne miejsce w matematyce ze względu na rolę, jaką odgrywają w geometrii rzutowej, ale tym razem tę sprawę pominiemy. Matematyka w nich zawarta zasadza się w tym, że rysunek spełniający podane warunki można wykonać bardzo łatwo i to na bardzo wiele różnych sposobów. Oto oryginalne przepisy twórców stosownych twierdzeń.
Twierdzenie (Girarda Desarguesa). Jeśli dwa trójkąty mają środek perspektywiczny, to mają też oś perspektywiczną.
Twierdzenie (Blaise'a Pascala, często również nazywane imieniem Pappusa). Punkty przecięcia przeciwległych boków sześciokąta wpisanego w dwie proste przecinają się na jednej prostej.
Objaśnienia
Mówimy, że trójkątyi
mają środek perspektywiczny, jeśli proste
dla
mają punkt wspólny; mówimy, że mają one oś perspektywiczną, gdy punkty przecięcia prostych
i
dla
leżą na jednej prostej. Sześciokąt wpisany w dwie proste to taki, którego kolejne wierzchołki leżą na innej z nich. Ponadto zakładamy, że dowolne proste przecinają się, co wymaga uzupełnienia płaszczyzny euklidesowej do rzutowej, ale wszystko, o czym będzie dalej mowa, będzie poprawne, jeśli ograniczymy się do sytuacji, w których prostych równoległych nie będzie.
Jak to się ma do konfiguracji w rysunku 1? Otóż, można na pierwszej z nich obrać dowolny punkt i odnaleźć na niej dwa trójkąty, dla których jest on ich środkiem perspektywicznym i prostą, która jest ich osią perspektywiczną. Podobnie druga konfiguracja wskazuje na możliwość swobodnego potraktowania jej jako ilustracji twierdzenia Pascala.
Pascal i Desargues ogłosili swoje twierdzenia niemal równocześnie. Powstał problem, czy przypadkiem jedno z nich nie implikuje drugiego w geometrii rzutowej. Po dwustu latach okazało się, że z twierdzenia Desarguesa nie wynika twierdzenie Pascala (w płaszczyźnie rzutowej nad kwaternionami jest Desargues, a nie ma Pascala). Po następnym pół wieku Gerhard Hessenberg udowodnił, że z twierdzenia Pascala wynika twierdzenie Desarguesa. I właśnie dowód tego faktu można przedstawić w czysto greckim stylu.
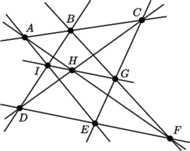
Rys. 2
Najpierw formalne wprawki. Konfigurację Pappusa będziemy oznaczać w następujący, zaproponowany przez Coxetera, sposób:

- jeśli punkty w pierwszym i drugim wierszu są współliniowe, oraz zachodzi "wyznacznikowa" zależność między ich elementami (czyli "przekątne" kolorowego prostokąta przecinają się w kolorowym punkcie trzeciego wiersza)

to punkty w trzecim wierszu też są współliniowe (Rys. 2).
A teraz zapowiedziany dowód.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (155 KB)