Elektryzująca metryka pingpongowa

Wśród wielu typów zagadnień matematycznych bardzo sobie cenię takie, które po wierzchu są elementarne, łatwe na początku i dające się rozwiązać nietypowymi, efektownymi, niecodziennymi metodami. Dobrze jest też, gdy zadania te są wierzchołkiem pewnej góry lodowej, albo – stosując inne porównanie – są początkiem ścieżki wiodącej nas w nieznane.
Zadanie 1. Mamy sześcian (a raczej jego szkielet), wykonany z drutu.
Do przeciwległych wierzchołków sześcianu podłączono prąd. Wyznaczyć
opór zastępczy układu. Zakładamy, że opór każdej krawędzi wynosi
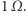
Jest to bardzo łatwe zadanie dla każdego, kto choć trochę zna prawa rządzące przepływem prądu. Nasuwa się od razu oczywiste uogólnienie: jak to jest dla innych wielościanów i ogólniej: dla innych układów. W latach sześćdziesiątych XX wieku wiele uwagi poświęcił podobnym zagadnieniom matematyk brytyjski i kanadyjski Crispin Alvah Nash-Williams (1932-2001).
Związek z geometrią dostrzegli tu przed stu laty E.E. Brooks i A.W. Poyser w książce Magnetism and Electricity. Jeden z najbardziej znanych popularyzatorów matematyki, Charles Wilderman Trigg 1898-1989), wracał do tego zadania kilkakrotnie, głównie na łamach Journal of Recreational Mathematics. Z jego artykułu w tym magazynie z roku 1981 pochodzi zadanie o oporze dla przeciwległych wierzchołków kostki dowolnego wymiaru. Potem zadanie zaczęło żyć własnym życiem i obrastać w teorię. Z zagadnieniami tymi można się zapoznać w sieci, na przykład pod hasłem resistance distance, co ja tłumaczę jako „odległość elektryczna”.
Od pewnego czasu wielościany (w szczególności foremne) sklejam z piłeczek pingpongowych. Jakoś lepiej mi się myśli, gdy mogę wziąć w rękę taki model. Stąd się wziął ten dziwny tytuł artykułu. Załączam zdjęcie sześcianu nad Giewontem.
Definicja. Niech
 będzie grafem spójnym. Wyobraźmy sobie,
że krawędzie jego są wykonane z materiału dobrze przewodzącego prąd
i że dana jest oporność każdej krawędzi. Dla dowolnych dwóch
wierzchołków grafu określamy ich odległość elektryczną jako opór
zastępczy całego układu, gdy do wierzchołków tych podłączony jest prąd.
będzie grafem spójnym. Wyobraźmy sobie,
że krawędzie jego są wykonane z materiału dobrze przewodzącego prąd
i że dana jest oporność każdej krawędzi. Dla dowolnych dwóch
wierzchołków grafu określamy ich odległość elektryczną jako opór
zastępczy całego układu, gdy do wierzchołków tych podłączony jest prąd.
Z praw dotyczących przepływu prądu otrzymujemy natychmiast, że
dla każdych trzech wierzchołków
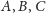 odległość między
odległość między
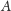 i
i
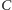 jest nie większa niż suma odległości między
jest nie większa niż suma odległości między
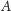 i
i
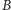 oraz między
oraz między
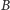 i
i
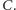 Znaczy to, że tak
określona odległość elektryczna jest rzeczywiście odległością w sensie
matematycznym i zbiór wierzchołków grafu tworzy pewną przestrzeń
metryczną, a konkretniej nawet wielościan.
Znaczy to, że tak
określona odległość elektryczna jest rzeczywiście odległością w sensie
matematycznym i zbiór wierzchołków grafu tworzy pewną przestrzeń
metryczną, a konkretniej nawet wielościan.
Zadanie może być sprowadzone do algebry. Mamy bowiem prawa Kirchhoffa:
I prawo Kirchhoffa. Suma natężeń prądów wpływających do węzła i z niego wypływających jest równa zeru. Inaczej mówiąc, ładunek elektryczny nie jest gromadzony w węźle.
II prawo Kirchhoffa. Suma spadków napięć na elementach obwodu zamkniętego jest równa zeru.
Mamy do dyspozycji też prawo Ohma oraz reguły rządzące opornością najprostszych typów połączeń oporników. Dla połączeń szeregowych opór zastępczy jest sumą oporów składowych, dla połączeń równoległych przepustowość układu jest równa sumie przepustowości składników. Przez przepustowość układu rozumiemy tu odwrotność oporu.
Równania Kirchhoffa nie są zwykle skomplikowane – jest ich jednak dużo. Gdzie tylko można, należy od nich uciekać, najczęściej odwołując się do geometrii. Możliwe to jest tam, gdzie układ cechuje pewna symetria. Rozpatrzmy uogólnienie zadania 1.
Zadanie 2. Wyznaczyć
opór zastępczy układu, gdy wejście i wyjście (źródło i ujście prądu)
są przeciwległymi wierzchołkami kostki
 -wymiarowej.
-wymiarowej.
Rozwiązanie. Wierzchołki odległe o tyle samo (w sensie odległości
„po grafie”) od tych punktów mają te same potencjały, więc nie popłynie
między nimi prąd. Dzięki temu możemy je utożsamić, co prowadzi do
układu połączonych ze sobą szeregowo
 podukładów połączeń
równoległych. Pozostaje określić, ile jest przewodów w każdym
z tych połączeń równoległych.
Jeżeli napięcie przyłożone jest w
podukładów połączeń
równoległych. Pozostaje określić, ile jest przewodów w każdym
z tych połączeń równoległych.
Jeżeli napięcie przyłożone jest w
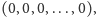 a ujście jest
w
a ujście jest
w
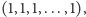 to wierzchołki są równoważne, gdy mają tę samą
sumę współrzędnych. Proste rozumowanie kombinatoryczne pokazuje, że
liczba krawędzi
wynosi kolejno
to wierzchołki są równoważne, gdy mają tę samą
sumę współrzędnych. Proste rozumowanie kombinatoryczne pokazuje, że
liczba krawędzi
wynosi kolejno
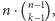 gdzie
gdzie
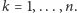 Na przykład, dla
sześcianu mamy kolejno 3, 6 i 3 połączenia, dla kostki wymiaru 4 mamy
kolejno 4, 12, 12 i 4 połączenia. Wynika stąd (po łatwych obliczeniach), że
opór zastępczy układu jest równy
Na przykład, dla
sześcianu mamy kolejno 3, 6 i 3 połączenia, dla kostki wymiaru 4 mamy
kolejno 4, 12, 12 i 4 połączenia. Wynika stąd (po łatwych obliczeniach), że
opór zastępczy układu jest równy

Opór ten maleje wykładniczo
wraz z wymiarem
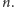 Czy jest to zgodne z naszą intuicją? Powinno
być: chociaż odległość między skrajnymi punktami rośnie liniowo, to
liczba połączeń rośnie wykładniczo.
Czy jest to zgodne z naszą intuicją? Powinno
być: chociaż odległość między skrajnymi punktami rośnie liniowo, to
liczba połączeń rośnie wykładniczo.
Przykład 1. Interesujące matematycznie jest
zadanie obliczenia oporu zastępczego szkieletu kostki
 -wymiarowej,
gdy źródło i ujście znajdują się w sąsiednich wierzchołkach
-wymiarowej,
gdy źródło i ujście znajdują się w sąsiednich wierzchołkach
Pełne wyliczenie pozostawimy Czytelnikowi. Wynik brzmi:
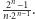 Opór
ten maleje wraz ze wzrostem
Opór
ten maleje wraz ze wzrostem
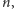 ale dość wolno. Znów możemy się
zastanowić, czy jest to zgodne z intuicją.
ale dość wolno. Znów możemy się
zastanowić, czy jest to zgodne z intuicją.
Często radzę uczniom i studentom tak: zmień fabułę zadania (nie zmieniając jego treści matematycznej) na inną, nawet żartobliwą lub niepoważną. Zrób to, po pierwsze, dla samego ćwiczenia. Otrzymasz – w terminologii wybitnego matematyka holenderskiego Hansa Freudenthala – zadanie izomorficzne. Po drugie, a nuż po takim przeformułowaniu zadanie będzie wyglądać ciekawiej i może nawet łatwiej się rozwiąże.
Wielu ludzi z pokolenia autora artykułu ma sentyment do kolei, najlepiej starych,
parowych, wlokących się dostojnie po szynach na drewnianych podkładach. No
to przełóżmy zadanie na język „kolejowy”, zamieniając je na problem
przepustowości sieci. Rozważę przypadek
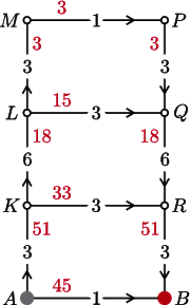
 Spójrzmy jeszcze
raz na diagram oczami dyspozytora kolejowego, który ma wysłać 96
wagonów ze stacji
Spójrzmy jeszcze
raz na diagram oczami dyspozytora kolejowego, który ma wysłać 96
wagonów ze stacji
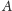 do stacji
do stacji
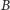 tak, by znalazły się tam
w jak najkrótszym czasie. Ma on do dyspozycji sieć stacji pośrednich
tak, by znalazły się tam
w jak najkrótszym czasie. Ma on do dyspozycji sieć stacji pośrednich
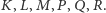 Czarne liczby 1, 3, 6 umieszczone na trasie oznaczają
przepustowość danej
Czarne liczby 1, 3, 6 umieszczone na trasie oznaczają
przepustowość danej
linii. Za jednostkę przepustowości weźmiemy odwrotność czasu przejazdu
jednego wagonu. Przepustowość 3 oznacza zatem, że w jednostce czasu da się
tym odcinkiem linii przesłać trzy wagony.
Dla młodszych Czytelników niech będą narty. Możemy sobie wyobrazić, że
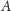 to podnóże góry,
to podnóże góry,
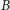 – wierzchołek a diagram to sieć
wyciągów. Niektóre z nich są wolniejsze, inne szybsze. Na przykład na odcinku
– wierzchołek a diagram to sieć
wyciągów. Niektóre z nich są wolniejsze, inne szybsze. Na przykład na odcinku
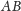 posuwamy się 3 razy wolniej niż na
posuwamy się 3 razy wolniej niż na
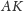 i
i
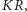 a sześć
razy wolniej niż na
a sześć
razy wolniej niż na
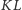 i
i
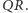 Na dole czeka 96 narciarzy. Jak
najszybciej wwieźć ich wszystkich na górę? Liczy się oczywiście czas, po
którym ostatni narciarz wjedzie na górę.
Na dole czeka 96 narciarzy. Jak
najszybciej wwieźć ich wszystkich na górę? Liczy się oczywiście czas, po
którym ostatni narciarz wjedzie na górę.
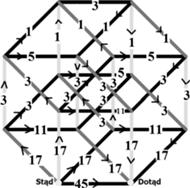
Rozwiążemy zadanie w interpretacji narciarskiej. 45 narciarzy wjeżdża trasą
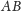 (czyli Stąd-Dotąd), jeden po drugim. Zajmuje im to łącznie 45 minut.
Pozostałych 51 narciarzy w 17 minut osiąga
(czyli Stąd-Dotąd), jeden po drugim. Zajmuje im to łącznie 45 minut.
Pozostałych 51 narciarzy w 17 minut osiąga
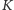 (na rysunku: drugi poziom).
Tu rozdzielają się, 33 jedzie do
(na rysunku: drugi poziom).
Tu rozdzielają się, 33 jedzie do
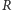 ; przy przepustowości 3 zajmuje im to
11 minut. W tym samym czasie 11 minut 15 turystów dociera do punktu
; przy przepustowości 3 zajmuje im to
11 minut. W tym samym czasie 11 minut 15 turystów dociera do punktu
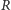 trasą
trasą
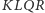 a trzech trasą
a trzech trasą
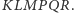 Po 45 minutach
wszyscy spotykają się na górze. Wyciągi pracowały bez przestojów, zatem jest to
najlepszy możliwy czas wykonania zadania. Wyciągi przewiozły zatem
96 turystów w 45 minut, co daje przepustowość
Po 45 minutach
wszyscy spotykają się na górze. Wyciągi pracowały bez przestojów, zatem jest to
najlepszy możliwy czas wykonania zadania. Wyciągi przewiozły zatem
96 turystów w 45 minut, co daje przepustowość
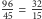 turysty na
minutę. Przepustowość to odwrotność oporu, zadanie rozwiązane,
odpowiedź jest zgodna z podaną wcześniej.
turysty na
minutę. Przepustowość to odwrotność oporu, zadanie rozwiązane,
odpowiedź jest zgodna z podaną wcześniej.
Metryką elektryczną zainteresowali się fizycy i chemicy (zwłaszcza krystalografowie). Odkryto metody algebraiczne, pozwalające na obliczenie wszystkich odległości elektrycznych dla konkretnego grafu. Niestety, obliczenia są skomplikowane. Należy bowiem rozważyć wszystkie połączenia w grafie, co prowadzi do rozważania macierzy o kilkunastu czy nawet kilkudziesięciu wierszach i kolumnach i obliczania ich macierzy odwrotnych, a to zawsze było skomplikowane rachunkowo. Ale my poprzestańmy na prostych grafach, gdzie – zabierając dziecku zabawkę – możemy bawić się kolejką elektryczną.