Deltoid
Sześciany i wielomiany
Ile wierzchołków, krawędzi, ścian dwuwymiarowych, trójwymiarowych etc.
ma
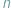 -wymiarowy sześcian?
-wymiarowy sześcian?

Rys. 1 Kolejne sześciany
 -wymiarowe. Na czarno i szaro narysowano poprzedni
sześcian i jego drugi egzemplarz, kolorem zaznaczono ślad przy przesuwaniu.
-wymiarowe. Na czarno i szaro narysowano poprzedni
sześcian i jego drugi egzemplarz, kolorem zaznaczono ślad przy przesuwaniu.
Przyjrzyjmy się dobrze znanym sześcianom zero-, jedno-, dwu- i trójwymiarowym. Sześcian zerowymiarowy to punkt – jeden wierzchołek. Sześcian jednowymiarowy to odcinek – dwa wierzchołki połączone krawędzią. Sześcian dwuwymiarowy to kwadrat – dwa odpowiednio połączone odcinki.
Można sobie wyobrażać, że sześcian
 -wymiarowy powstaje
z sześcianu
-wymiarowy powstaje
z sześcianu
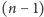 -wymiarowego przez przesunięcie go w
-wymiarowego przez przesunięcie go w
 -tym
wymiarze (Rys. 1). Ma więc dwukrotnie więcej wierzchołków, krawędzi i ścian
każdego wymiaru (odpowiadających początkowemu i końcowemu położeniu
przesuwanego sześcianu), a dodatkowo ma krawędzie i ściany otrzymane jako
ślady przy przesuwaniu. Wierzchołek jako swój ślad pozostawia krawędź,
śladem krawędzi jest ściana dwuwymiarowa i ogólniej, śladem ściany
-tym
wymiarze (Rys. 1). Ma więc dwukrotnie więcej wierzchołków, krawędzi i ścian
każdego wymiaru (odpowiadających początkowemu i końcowemu położeniu
przesuwanego sześcianu), a dodatkowo ma krawędzie i ściany otrzymane jako
ślady przy przesuwaniu. Wierzchołek jako swój ślad pozostawia krawędź,
śladem krawędzi jest ściana dwuwymiarowa i ogólniej, śladem ściany
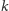 -wymiarowej jest ściana
-wymiarowej jest ściana
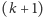 -wymiarowa.
-wymiarowa.
Istotnie, sześcian trójwymiarowy, otrzymany jako przesunięcie przedniej kwadratowej ściany tak, by uzyskać tylną, ma:
-
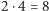 wierzchołków (dwukrotność tego, co kwadrat),
wierzchołków (dwukrotność tego, co kwadrat),
-
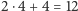 krawędzi (dwukrotność tego, co kwadrat,
plus liczba wierzchołków kwadratu – powstały z nich krawędzie
łączące przód i tył),
krawędzi (dwukrotność tego, co kwadrat,
plus liczba wierzchołków kwadratu – powstały z nich krawędzie
łączące przód i tył),
-
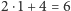 ścian dwuwymiarowych
(dwukrotność tego, co kwadrat, plus liczba krawędzi kwadratu –
powstały z nich ściany górna, dolna, prawa i lewa),
ścian dwuwymiarowych
(dwukrotność tego, co kwadrat, plus liczba krawędzi kwadratu –
powstały z nich ściany górna, dolna, prawa i lewa),
- jedną ścianę trójwymiarową (wnętrze, otrzymane jako ślad wnętrza przesuwanego kwadratu).

Rys. 2
 – wymiar sześcianu,
– wymiar sześcianu,
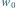 – liczba wierzchołków,
– liczba wierzchołków,
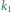 – krawędzi,
– krawędzi,
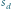 – ścian
– ścian
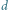 -wymiarowych.
-wymiarowych.
Podsumowując, stwórzmy tabelę (Rys. 2). Wartości w kolejnym wierszu powstają przez podwojenie poprzednich i dodanie do tego poprzednich przesuniętych o jedno miejsce. Tą metodą otrzymujemy ostatni z wypisanych wierszy, dla sześcianu czterowymiarowego. Podobnie można wyznaczać dalsze wartości, choć szukanie w ten sposób np. liczby 19-wymiarowych ścian w sześcianie 42-wymiarowym byłoby dość nużące.
Sumy liczb w kolejnych wierszach to 1, 3, 9, 27, 81 – potęgi trójki. Tak być musi, bo każdy wyraz poprzedniego wiersza wliczany jest w następnym wierszu trzykrotnie: raz podwojony i jeszcze raz, po przesunięciu, dodany.
Na przemian dodając i odejmując wyrazy, uzyskujemy w wierszach 1,
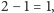
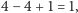
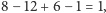
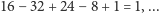 Czy
dalej też wychodzi 1?
Czy
dalej też wychodzi 1?
Rozważmy wielomiany
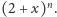 Dla
Dla
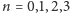 mamy:
mamy:

Następny wiersz powstaje z poprzedniego poprzez pomnożenie przez
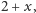 czyli pomnożenie poprzedniego wiersza przez 2 oraz dodanie
do tego poprzedniego wiersza pomnożonego przez
czyli pomnożenie poprzedniego wiersza przez 2 oraz dodanie
do tego poprzedniego wiersza pomnożonego przez
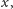 a więc
„przesuniętego”.
a więc
„przesuniętego”.
Współczynniki wyżej wypisanych wielomianów są takie same, jak liczby w początkowych wierszach tabeli z rysunku 2 W następnych wierszach też uzyskamy tutaj takie same liczby, jak tam, bo procedura ich tworzenia jest identyczna. Stąd
liczba
-wymiarowych ścian w
-wymiarowym sześcianie to współczynnik przy
w wielomianie
czyli
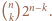
Sześcian 42-wymiarowy ma więc

ścian 19-wymiarowych.
Suma liczb w
 -tym wierszu rysunku 2 to suma współczynników
wielomianu
-tym wierszu rysunku 2 to suma współczynników
wielomianu
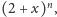 czyli jego wartość dla
czyli jego wartość dla
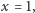 a więc
a więc
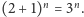
Z kolei naprzemienna suma liczb z
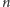 -tego wiersza to wartość tego
wielomianu dla
-tego wiersza to wartość tego
wielomianu dla
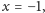 czyli
czyli
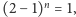 zatem faktycznie zawsze
równa jest 1.
zatem faktycznie zawsze
równa jest 1.
 -wymiarowe. Na czarno i szaro narysowano poprzedni
sześcian i jego drugi egzemplarz, kolorem zaznaczono ślad przy przesuwaniu.
-wymiarowe. Na czarno i szaro narysowano poprzedni
sześcian i jego drugi egzemplarz, kolorem zaznaczono ślad przy przesuwaniu.
 – wymiar sześcianu,
– wymiar sześcianu,
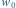 – liczba wierzchołków,
– liczba wierzchołków,
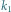 – krawędzi,
– krawędzi,
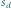 – ścian
– ścian
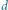 -wymiarowych.
-wymiarowych.