Powierzchnie: zajęcia praktyczno–techniczne
Wstęgą Möbiusa nazywamy powierzchnię z brzegiem otrzymaną z prostokąta w wyniku sklejenia jednej pary jego przeciwległych boków w pewien sposób...
Zauważmy, że brzeg wstęgi Möbiusa jest pojedynczą krzywą zamkniętą. W przyszłości potrzebna nam będzie następująca obserwacja: odcinając od wstęgi Möbiusa cienki pierścień, przylegający do jej brzegu, otrzymujemy znowu wstęgę Möbiusa (patrz rysunek 1c).
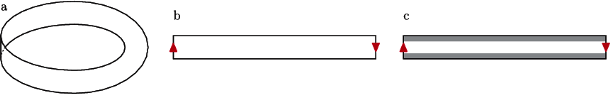
Rys. 1 Konstrukcja wstęgi Möbiusa

Rys. 2
Torusem nazywamy powierzchnię bez brzegu otrzymaną z prostokąta (lub innego równoległoboku) przez sklejenie dwóch par przeciwległych boków w sposób zaznaczony na rysunku 2a. W „przyrodzie” torus pojawia się m.in. jako powierzchnia dętki samochodowej albo amerykańskiego pączka (Rys. 2b).

Rys. 3
Jaką powierzchnię otrzymujemy, sklejając trzy pary przeciwległych boków sześciokąta foremnego, w sposób zaznaczony na rysunku 3? Jeśli wykorzystamy sześciokątną siatkę na płaszczyźnie, to przekonamy się, że otrzymujemy torus. Mianowicie, dzielimy sześciokąt na cztery części (patrz rysunek 4) i przeklejamy je zgodnie z siatką, otrzymując równoległobok z odpowiednimi sklejeniami.
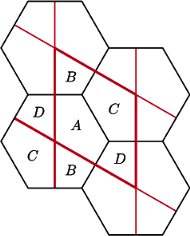
Rys. 4
Ten artykuł jest poświęcony dowodowi następującego lematu, który jest ważnym elementem klasyfikacji powierzchni. Zainteresowanym zastosowaniem tego lematu do twierdzenia klasyfikacyjnego polecamy rozdział 12.4 książki R. Engelkinga i K. Siekluckiego Geometria i topologia, część II. Tych, którzy z poniższym lematem się już zetknęli, zachęcamy do porównania naszego dowodu z dowodem, który znają.
Lemat. Po wycięciu z torusa koła i przyklejeniu do otrzymanej powierzchni wzdłuż brzegu wstęgi Möbiusa otrzymamy tę samą powierzchnię, co po wycięciu ze sfery trzech kół i wklejeniu na ich miejsce trzech wstęg Möbiusa.
Dowód. Krok I. Zauważmy, że powierzchnia otrzymana ze sfery przez wycięcie trzech kół i wklejenie na ich miejsce trzech wstęg Möbiusa powstaje z sześciokąta foremnego po sklejeniu jego boków w sposób przedstawiony na rysunku 5a: trzy wstęgi Möbiusa zaznaczone są na rysunku 5b (gdzie każdy bok sześciokąta został podzielony na trzy odcinki równej długości).
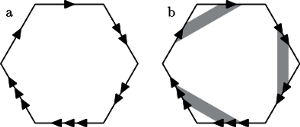
Rys. 5
Pozostawiamy Czytelnikowi przekonanie się, że po usunięciu tych trzech wstęg Möbiusa dostajemy sferę z wyciętymi trzema kołami.
Krok II. Dzielimy sześciokąt z poprzedniego kroku (rysunek 5a) na trzy części jak na rysunku 6a i sklejamy je wzdłuż fragmentów ich brzegu pochodzących z brzegu wyjściowego sześciokąta. Rezultat dwóch z tych klejeń widzimy na rysunku 6b (jedną z części odwróciliśmy na drugą stronę). Po wykonaniu trzeciego klejenia otrzymujemy wstęgę Möbiusa, na której brzegu zaznaczono, które fragmenty należy skleić, by otrzymać wyjściową powierzchnię, patrz rysunek 6c.
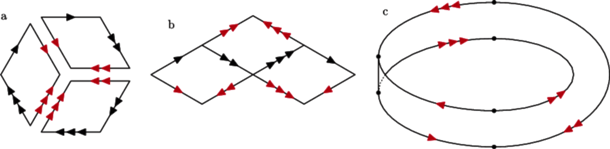
Rys. 6

Rys. 7
Krok III. We wstędze Möbiusa, otrzymanej w poprzednim kroku, rozważamy teraz cienki pierścień przyległy do brzegu. Dzięki obserwacji z początku artykułu powierzchnia, którą badamy, powstaje z tego pierścienia przez doklejenie do jednej składowej jego brzegu wstęgi Möbiusa i sklejenie drugiej składowej jego brzegu tak, jak brzegu wstęgi Möbiusa z rysunku 6c, patrz rysunek 7 Jeśli ten rysunek porównamy z rysunkiem 3, to stwierdzimy, że nasza powierzchnia jest torusem, z którego wycięliśmy koło i zastąpiliśmy wstęgą Möbiusa, co kończy dowód.