Słowa, słowa, słowa...
Słowa, którymi będziemy się zajmowali, będą napisami złożonymi z liter jednego lub kilku zbiorów (na początek przyjmijmy, że zbiory są dwa – jeden zawiera małe litery łacińskie, a drugi duże) o tej własności, że dwie jednakowe litery umieszczone po kolei będą znikały. Napis, w którym wszystko znikło (czasem i taki jest potrzebny), będzie oznaczany 1.
Przykład. Zbiór
jest jeden, a litery są dwie:
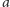 i
i
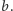 Wprowadzamy dodatkowy
warunek
Wprowadzamy dodatkowy
warunek
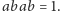 Co opisują te słowa?
Co opisują te słowa?
Algebraik odpowie: to grupa Kleina, czteroelementowa grupa niecykliczna.
Geometra
stwierdzi, że to grupa izometrii własnych prostokąta, czyli sposobów
położenia banknotu na jego obrysie.
Słowo grupa jest dobrze dobrane do naszych słów. Faktycznie, dopisywanie
jednego do drugiego można traktować jak działanie (będziemy o nim
mówić: mnożenie). Elementem neutralnym jest wtedy 1, a elementem
przeciwnym do
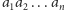 jest
jest
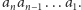 Łączność
dopisywania nie wymaga uzasadnień. Zatem nasze słowa przy dowolnym
wyborze zbiorów liter tworzą grupę.
Łączność
dopisywania nie wymaga uzasadnień. Zatem nasze słowa przy dowolnym
wyborze zbiorów liter tworzą grupę.
W tej terminologii wszystkie litery są inwolucjami (czyli są odwrotne do siebie) i dlatego takie grupy nazywają się inwolutywne.
Grupy takie mogą się różnić nie tylko zbiorami liter, ale też dodatkowymi warunkami pozwalającymi (jak w powyższym przykładzie) skracać słowa.
Fanaberia Leibniza, czyli motywacja historyczna
Gottfried Friedrich Wilhelm Leibniz (1646-1716) ogromną wagę przywiązywał do języka, w jakim formułuje się prawa każdej z dyscyplin nauki – twierdził, że każda dyscyplina powinna mieć własny. W szczególności twierdził, że geometria analityczna to odrażająca hybryda: do geometrii używa się języka algebry. W geometrii można liczyć, ale na obiektach geometrycznych – twierdził.
Nikt nie brał tego postulatu poważnie, aż pod koniec XIX wieku Juhasson Hjelmslev (1873-1950) stwierdził, że można rachować na podprzestrzeniach, utożsamiając je z symetriami względem tych podprzestrzeni. Przyjrzyjmy się temu na płaszczyźnie.
Co dla różnych prostych
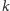 i
i
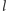 oznacza napis
oznacza napis
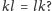 Chwila
namysłu pozwoli nam zauważyć, że złożenie dwóch symetrii osiowych to
przesunięcie (ale wtedy obie strony oznaczałyby przesunięcia w przeciwnych
kierunkach) lub obrót. Zatem rozważana równość to stwierdzenie, że dwa
obroty o ten sam kąt, ale o przeciwnym zwrocie, są równe: co to za kąt?
Oczywiście, kąt półpełny! Zatem proste muszą tworzyć kąt o połowę
mniejszy, czyli są prostopadłe.
Chwila
namysłu pozwoli nam zauważyć, że złożenie dwóch symetrii osiowych to
przesunięcie (ale wtedy obie strony oznaczałyby przesunięcia w przeciwnych
kierunkach) lub obrót. Zatem rozważana równość to stwierdzenie, że dwa
obroty o ten sam kąt, ale o przeciwnym zwrocie, są równe: co to za kąt?
Oczywiście, kąt półpełny! Zatem proste muszą tworzyć kąt o połowę
mniejszy, czyli są prostopadłe.
Proste spełniające podany warunek mają jeszcze i tę własność, że dla
pewnego punktu
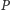 (nie ukrywajmy – punktu ich przecięcia) mamy
równość
(nie ukrywajmy – punktu ich przecięcia) mamy
równość
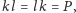 bo przecież obrót o kąt półpełny to symetria
względem środka obrotu.
bo przecież obrót o kąt półpełny to symetria
względem środka obrotu.
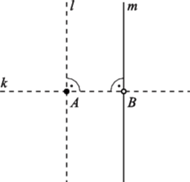
Rys. 1 Oba przekształcenia to symetrie z poślizgiem (czyli złożenia symetrii z przesunięciem
o wektor równoległy do jej osi). Że przesunięcia są przeciwne, łatwo zauważyć
pisząc
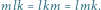 Jeśli to obustronnie pomnożymy przez
Jeśli to obustronnie pomnożymy przez
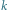 (i
(i
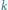 zniknie), to otrzymamy
zniknie), to otrzymamy
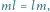 czyli dwa przeciwne przesunięcia.
czyli dwa przeciwne przesunięcia.
Co wobec tego oznacza napis
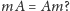 Spójrzmy na rysunek 1.
Dobierając proste
Spójrzmy na rysunek 1.
Dobierając proste
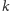 i
i
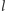 tak, by było
tak, by było
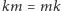 oraz
oraz
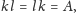 otrzymujemy
otrzymujemy
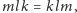 a więc prawa strona
badanej równości to złożenie symetrii względem
a więc prawa strona
badanej równości to złożenie symetrii względem
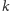 z przesunięciem
o wektor
z przesunięciem
o wektor
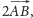 podczas gdy lewa to złożenie przesunięcia
o
podczas gdy lewa to złożenie przesunięcia
o
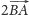 z symetrią względem
z symetrią względem
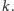 To jest to samo tylko wtedy, gdy
To jest to samo tylko wtedy, gdy
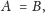 czyli badany napis oznacza, że
czyli badany napis oznacza, że
 leży na
leży na
Można by zatem – wobec tych obserwacji – podejrzewać, że za pomocą wprowadzonych na początku słów potrafimy w szczególności opisać geometrię płaszczyzny. I tak jest w istocie.
Kończąc dygresję historyczną, wypada powiedzieć, że kluczowym pojęciem
pozwalającym na zrealizowanie fanaberii Leibniza było wyróżnienie zbioru
liter przemiennych z daną literą –
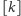 oznaczać będzie dalej zbiór liter
przemiennych z
oznaczać będzie dalej zbiór liter
przemiennych z
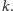 To pojęcie wprowadził i zastosował Arnold
Schmidt (1902-1967), a sprawę doprowadził do końca Friedrich Bachmann
(1909-1982).
To pojęcie wprowadził i zastosował Arnold
Schmidt (1902-1967), a sprawę doprowadził do końca Friedrich Bachmann
(1909-1982).
Nauka obcego języka
Wiemy już, co w geometrii płaszczyzny oznacza
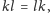 a co
a co
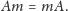 Aby zobaczyć, jak wygląda tak opisywana geometria, trzeba
przejść przynajmniej krótkie samokształcenie w używaniu leibnizowskiego
języka.
Aby zobaczyć, jak wygląda tak opisywana geometria, trzeba
przejść przynajmniej krótkie samokształcenie w używaniu leibnizowskiego
języka.
Proszę odpowiedzieć na pytanie, co oznaczają następujące napisy:

Odpowiedzi znajdują się w numerze, ale proszę się postarać samodzielnie odczytać znaczenia. Wtedy stanie się jasne, że zmiana języka to poniekąd zmiana patrzenia na świat: to, co w uświęconym tradycją klasycznym szkolnym języku geometrii wyraża się prosto, tu może wyrażać się bardziej zawile, ale jest i odwrotnie – trudno formułowalne w języku klasycznym sytuacje po leibnizowsku niejednokrotnie będą bardzo proste.
Choćby taki fakt: słowo
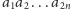 daje się zawsze zastąpić słowem
dwuliterowym i wynikający stąd natychmiast wniosek, że każde słowo ma
odpowiednik co najwyżej trzyliterowy. Co to znaczy geometrycznie? I jak to
udowodnić?
daje się zawsze zastąpić słowem
dwuliterowym i wynikający stąd natychmiast wniosek, że każde słowo ma
odpowiednik co najwyżej trzyliterowy. Co to znaczy geometrycznie? I jak to
udowodnić?
Okazuje się, że w tej sprawie kluczowy (i wystarczający) jest fakt:
Fakt. Jeśli
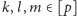 lub
lub
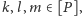 to istnieje takie
to istnieje takie
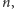 że
że
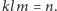
Przesłanki powyższego zdania klasycznie brzmią:
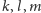 są
współpękowe (prawda?). Ale takie spojrzenie pozwala nam na naturalne
uogólnienie, że zbiór liter nazwiemy pękiem, gdy każdy trzyliterowy napis
złożony z liter należących do tego zbioru da się zastąpić napisem
jednoliterowym. Proszę sprawdzić, że punkty przestrzeni euklidesowej
dowolnego wymiaru tworzą pęk (jak by to brzmiało klasycznie?).
są
współpękowe (prawda?). Ale takie spojrzenie pozwala nam na naturalne
uogólnienie, że zbiór liter nazwiemy pękiem, gdy każdy trzyliterowy napis
złożony z liter należących do tego zbioru da się zastąpić napisem
jednoliterowym. Proszę sprawdzić, że punkty przestrzeni euklidesowej
dowolnego wymiaru tworzą pęk (jak by to brzmiało klasycznie?).
Czasami tłumaczenie bywa twórcze. Na przykład zdanie, które orzeka, że dla
dowolnych liter
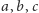 zachodzi
zachodzi

pełni rolę tzw. słowa Banacha, czyli pozwala stwierdzić, że w grupie izometrii płaszczyzny euklidesowej nie istnieją podgrupy wolne, co m.in. wyklucza paradoksalny rozkład na płaszczyźnie. Oryginalne słowo Banacha to twierdzenie:
Twierdzenie. Dla dowolnych izometrii płaszczyzny euklidesowej
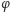 i
i
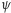 przekształcenie
przekształcenie

jest identycznością.
Które sformułowanie jest prostsze?
Kolejny przykład to
Twierdzenie (Michela Chasles’a). każda izometria jest postaci
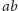 lub
lub
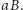
Chasles wyrażał to w następujący sposób:
Twierdzenie. Każda izometria płaszczyzny jest przesunięciem, obrotem lub symetrią z poślizgiem.
(Równoważność obu sformułowań była już obecna w tekście tego artykułu).
Argumentem za tym, że pierwsze ze sformułowań jest bardziej nośne, może być fakt, iż Bachmann pod jego inspiracją stworzył odrębny dział teorii grup: grupy biinwolutywne, czyli takie, w których każdy z elementów jest inwolucją lub złożeniem dwu inwolucji. Do badania tego rodzaju obiektów może zachęcić spostrzeżenie, że
Fakt. Grupa izometrii przestrzeni euklidesowej dowolnego wymiaru jest biinwolutywna.
czy jeszcze bardziej niespodziewane, że biinwolutywna jest też grupa bijekcji dowolnego zbioru.
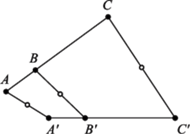
Rys. 2

Rys. 3
Czy odmienny punkt widzenia pozwala zobaczyć coś nowego
Podam przykład problemu łatwego w stylu leibnizowskim i trudnego w stylu klasycznym. Co więcej – klasycznie trudno było nawet wpaść na pomysł, że taka prawidłowość może mieć miejsce.
Twierdzenie (Hjelmsleva). Jeśli
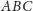 i
i
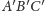 są
przystającymi trójkami punktów współliniowych, to środki odcinków
są
przystającymi trójkami punktów współliniowych, to środki odcinków
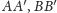 i
i
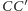 leżą na jednej prostej (Rys. 2).
leżą na jednej prostej (Rys. 2).
Dowód. Odcinek
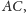 a więc punkty
a więc punkty
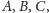 można
nałożyć na
odcinek
można
nałożyć na
odcinek
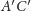 dwiema izometriami: jedną z nich będzie obrót lub
przesunięcie, a drugą symetria z poślizgiem. W symetrii z poślizgiem
zaś środek każdej pary punkt-obraz leży na jej osi (Rys. 3).
dwiema izometriami: jedną z nich będzie obrót lub
przesunięcie, a drugą symetria z poślizgiem. W symetrii z poślizgiem
zaś środek każdej pary punkt-obraz leży na jej osi (Rys. 3).
***
Pełny i zaawansowany wykład demonstrujący wykorzystanie tego języka można znaleźć w monografii Bachmanna Aufbau der Geometrie aus dem Spiegelungsbegrieff, Springer, 1959. Ale jest pytanie, czy ktoś normalny, a zatem niebędący zawodowym matematykiem, z tego języka korzysta. Okazuje się, że tak – program geometrii w szkołach niemieckich korzysta z tego języka. Możemy się o tym przekonać, zaglądając do wydanego przez Prószyńskiego poradnika pod nazwą Atlas matematyki, będącego tłumaczeniem szkolnego poradnika używanego w Niemczech – geometria w nim jest mocno odmienna od tej, jaką znamy ze szkoły.
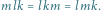 Jeśli to obustronnie pomnożymy przez
Jeśli to obustronnie pomnożymy przez
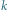 (i
(i
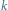 zniknie), to otrzymamy
zniknie), to otrzymamy
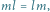 czyli dwa przeciwne przesunięcia.
czyli dwa przeciwne przesunięcia.