1. Wycinanie

W pierwszym kroku doświadczenia wytnijmy cokolwiek, np. lewą górną ćwiartkę kartki. To było proste, ale szybko dostrzegamy techniczny problem polegający na tym, że będziemy musieli decydować, co wyciąć w drugim kroku wycinania, i w następnym, i w następnym... Dobrze byłoby znaleźć jakąś metodę, dzięki której nie musielibyśmy podejmować decyzji i która uprościłaby całe doświadczenie. Usunięcie lewej górnej ćwiartki ma nieoczekiwanie pozytywne konsekwencje. Wszak pozostały nam w ręku trzy kwadratowe ćwiartki i możemy z nimi postąpić podobnie – usunąć z każdej z nich jej lewą górną ćwiartkę. To, co zostanie, będzie sumą większej już liczby „ćwiartek ćwiartek”, z którymi – dzięki naszej metodzie – poradzimy sobie bez trudu. Na każdym kroku wycinania będziemy wiedzieli, co wyciąć, nawet jeśli zechcemy wykonać tych kroków nieskończenie wiele. To zaś nieuchronnie nastąpi – wszak przeprowadzamy doświadczenie myślowe.

Rysunek obok przedstawia dobre przybliżenie naszej pierwszej nieskończonej wycinanki. Przyglądając się mu uważnie, można dostrzec pewną własność nieskończonej wycinanki, której nie mają jej kolejne przybliżenia, a która jest konsekwencją wybranej metody wycinania. Skoro w trzech częściach wycinanki nasze nożyczki pracowały podobnie do tego, jak wycinały całą wycinankę, to każda z tych części jest podobna do całej wycinanki. To podobieństwo ma już jednak sens ściśle geometryczny, tzn.:

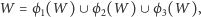
gdzie 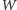 jest wycinanką, a 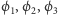 to trzy podobieństwa (w tym przypadku jednokładności) przekształcające kwadrat w jego odpowiednie ćwiartki. Własność figury 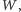 polegająca na tym, że jest ona sumą podobnych do siebie fragmentów, nazywa się samopodobieństwem.

Opanowawszy zdziwienie, że tak prosta procedura prowadzi do tak skomplikowanego kształtu, prawdziwy „doświadczalnik” znalazł już zapewne pole do dalszych doświadczeń. Kwadrat jest przecież podobny do swojej ćwiartki na 8 różnych sposobów. Każde z takich podobieństw jest złożeniem jednokładności o środku w wierzchołku kwadratu z jedną z ośmiu izometrii własnych kwadratu (czterech symetrii osiowych lub czterech obrotów).

Czy, wybrawszy dowolny z 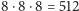  układów trzech podobieństw 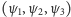 przekształcających kwadrat w trzy ustalone ćwiartki, można tak „zaprogramować” nożyczki, żeby wycinanka 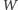 była sumą swoich kopii, czyli

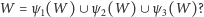
Pozytywnej (ale i znacznie ogólniejszej) odpowiedzi na to pytanie dostarcza twierdzenie Hutchinsona z 1982 roku, o którym pisze dokładniej Przemysław Kiciak w artykule Układy iterowanych przekształceń.

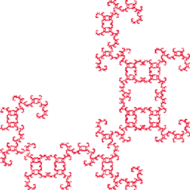
Czy – pytając dalej – wszystkie tak powstałe wycinanki będą istotnie różne (tzn. nieizometryczne)? Odpowiedź na to pytanie jest bardzo prosta. Wskazówką niech będzie przykład wycinanki, która jest samopodobna na przynajmniej 4096 sposobów. Wystarczy w pierwszym kroku wyciąć „nic”, by następnie z każdą z czterech pozostałych ćwiartek postąpić podobnie (na 8 różnych sposobów) i powtórzyć tę czynność (dla porządku jedynie) nieskończenie wiele razy.

Na marginesach (nie tylko tego artykułu) prezentujemy niektóre spośród 512 wycinanek powstałych w opisany powyżej sposób. Nie zawsze łatwo zgadnąć, jakich podobieństw użyto do ich wykonania. Jeśli ktoś to zrobi bez użycia linijki, to na pewno ma doskonale wygimnastykowane oko. W Albumie można obejrzeć wszystkie wycinanki powstające w opisany wyżej sposób.

2. Pomiary.

W każdym doświadczeniu, nawet myślowym, powinno się dokonać jakichś pomiarów. Spróbujmy zatem zmierzyć wycinanki. W zasięgu ręki mamy linijkę (przyrząd do mierzenia długości) i przyrząd do mierzenia pola powierzchni. Niestety, szybko okazuje się, że nasza wycinanka ma nieskończoną długość – wystarczy dodać długości wszystkich odcinków w niej zawartych. Równie szybko dochodzimy do wniosku, że wycinanka ma zerowe pole – wystarczy dodać pola wycinanych ćwiartek i porównać z polem kartki, od której zaczynaliśmy. Mamy również nieodparte wrażenie, że nasze wycinanki są w pewnym sensie bardziej skomplikowane niż typowe figury dodatniej długości i mniejsze niż figury o dodatnim polu.

Intuicja podpowiada nam, że użyliśmy niewłaściwych przyrządów – tak, jak to się czasem dzieje w życiu codziennym, np. wtedy, gdy próbujemy się zważyć na wadze aptekarskiej lub na wadze do ważenia parowozów. Jeden z przyrządów jest za czuły, a drugi w ogóle nie reaguje.

Czy istnieje przyrząd pomiarowy odpowiedni dla wycinanek?

Posługując się jedynie intuicją, szybko pokażemy, jak powinien ów przyrząd wyglądać (jeśli istnieje, oczywiście). Zauważmy najpierw, że zarówno długość, jak i pole mają coś wspólnego z wymiarem topologicznym. Dodatnią długość miewają figury 1-wymiarowe (ich pole jest na pewno zerowe), a dodatnie pole miewają figury 2-wymiarowe (ich długość jest na pewno nieskończona). Szukamy takiej miary, która przy próbie zmierzenia wycinanki dawałaby wynik dodatni – jej „czułość”  powinna być pomiędzy 1 a 2, tzn. pomiary tą miarą figur 1-wymiarowych powinny dawać wynik 0, a figur 2-wymiarowych  Oznaczmy tę hipotetyczną miarę przez 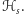 W konstrukcji naszej wycinanki główną rolę odgrywały podobieństwa. Wiemy, że długość zmienia się proporcjonalnie do pierwszej potęgi skali podobieństwa, a pole – do jej kwadratu. Możemy więc oczekiwać, że nasza hipotetyczna miara 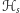 będzie się zmieniać proporcjonalnie do skali podobieństwa w potędze 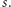 Jeśli zatem istnieje właściwa miara o czułości 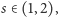 która dla naszej wycinanki przyjmuje wartość dodatnią, a ponadto przy podobieństwach zmienia się w sposób analogiczny do długości i pola przekształcanych figur, to

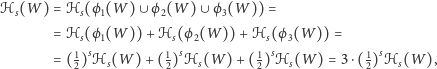
czyli (skoro przyjęliśmy, że 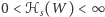) parametr  musi spełniać równanie 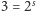 i ostatecznie 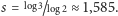 Ten wynik doskonale potwierdzałby naszą intuicję, że Świat (przynajmniej wycinanek) nie jest całkiem bez sensu. Potwierdzałby, gdyby miara 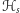 rzeczywiście istniała...

3. Na zakończenie

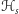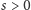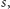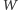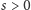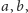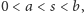Miary  dla  istnieją i noszą nazwę miar Hausdorffa. Parametr  który roboczo nazywaliśmy czułością miary, nazywa się wymiarem Hausdorffa. Jeśli dla pewnej figury  i liczby  oraz takich dowolnych liczb  że  mamy 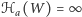 oraz 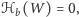 to mówimy, że figura 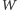 ma wymiar Hausdorffa 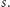 Jeśli wymiar Hausdorffa figury 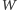 jest różny od jej wymiaru topologicznego, to 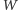 jest fraktalem. Każda z 512 naszych wycinanek jest fraktalem o wymiarze Hausdorffa równym

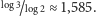
Dziwne to uczucie wiedzieć, że nie mówimy prozą...