Symetryzacja Steinera
Prosta operacja symetryzacji pozwala w elementarny sposób rozwiązywać nieelementarne problemy...
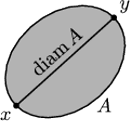
Rys. 1 Średnica zbioru mierzy, jak duży on jest.
Rozważmy wypukłą bryłę
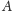 w przestrzeni trójwymiarowej
w przestrzeni trójwymiarowej
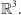 Jedną z wielkości charakteryzujących to, jak duża jest bryła, może być jej
średnica, którą oznaczamy przez
Jedną z wielkości charakteryzujących to, jak duża jest bryła, może być jej
średnica, którą oznaczamy przez
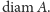 Jest to kres górny
odległości
Jest to kres górny
odległości
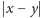 pomiędzy dowolną parą punktów
pomiędzy dowolną parą punktów
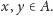 Na
przykład, średnica sześcianu
Na
przykład, średnica sześcianu
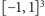 o wierzchołkach w punktach
o wierzchołkach w punktach
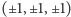 wynosi
wynosi
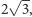 bowiem dwa najbardziej oddalone od
siebie punkty to np. wierzchołki
bowiem dwa najbardziej oddalone od
siebie punkty to np. wierzchołki
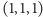 i
i
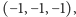 które są
odległe o
które są
odległe o
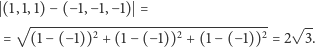
Zauważmy też, że zgodnie z tą definicją, średnica kuli o promieniu
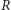 to
to
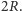
Czy bryła
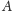 o ustalonej średnicy
o ustalonej średnicy
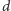 może mieć dowolnie dużą
objętość
może mieć dowolnie dużą
objętość
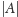 ? Oczywiście, że nie, bo z definicji średnicy
zbioru bryła
? Oczywiście, że nie, bo z definicji średnicy
zbioru bryła
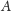 musi być zawarta w kuli o promieniu
musi być zawarta w kuli o promieniu
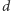 i środku w dowolnie wybranym punkcie
i środku w dowolnie wybranym punkcie
 bryły. Zapytajmy
dalej.
bryły. Zapytajmy
dalej.
Pytanie 1. Które spośród wszystkich brył wypukłych
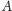 o ustalonej
średnicy
o ustalonej
średnicy
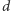 mają największą objętość i ile ona wynosi?
mają największą objętość i ile ona wynosi?

Rys. 2 Symetryzacja Steinera względem płaszczyzny
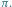
Jest to tzw. problem izodiametryczny. Można go łatwo rozwiązać przy użyciu
silnego geometrycznego narzędzia, jakim jest tytułowa symetryzacja. Dla bryły
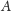 jej symetryzacja Steinera
jej symetryzacja Steinera
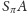 względem płaszczyzny
względem płaszczyzny
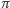 to
zbiór powstały przez zastąpienie każdego cięcia
to
zbiór powstały przez zastąpienie każdego cięcia
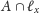 zbioru
zbioru
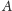 prostą
prostą
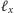 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny
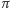 i przechodzącą przez punkt
i przechodzącą przez punkt
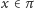 odcinkiem o środku w punkcie
odcinkiem o środku w punkcie
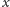 i długości równej
długości odcinka
i długości równej
długości odcinka
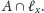 Jeśli ktoś lubi znaczki, to zapisujemy to
formalnie tak
Jeśli ktoś lubi znaczki, to zapisujemy to
formalnie tak
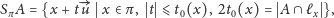
gdzie
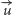 jest ustalonym jednostkowym wektorem prostopadłym do obranej
na samym początku płaszczyzny
jest ustalonym jednostkowym wektorem prostopadłym do obranej
na samym początku płaszczyzny
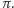
Intuicyjnie, niezależnie nad każdym punktem
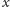 płaszczyzny
płaszczyzny
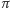 tak
przesuwamy fragment bryły, żeby był on symetryczny względem płaszczyzny
tak
przesuwamy fragment bryły, żeby był on symetryczny względem płaszczyzny
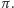 Ta operacja ma takie kluczowe własności:
Ta operacja ma takie kluczowe własności:
- (i)
- zachowuje wypukłość – jeśli
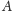 jest bryłą wypukłą, to
jest bryłą wypukłą, to
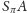 też,
też,
- (ii)
- bryła
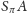 jest symetryczna względem płaszczyzny
jest symetryczna względem płaszczyzny
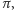
- (iii)
- nie zmienia objętości bryły –
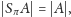
- (iv)
- nie powiększa średnicy –
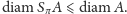
Rys. 3 Symetryzacja Steinera nie powiększa średnicy zbioru.
Własność (ii) jest jasna z konstrukcji zbioru
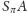 ; (iii) podobnie, bo
nalewając wody do
; (iii) podobnie, bo
nalewając wody do
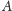 i do
i do
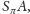 nalejemy jej tyle samo, gdyż nad
każdym punktem
nalejemy jej tyle samo, gdyż nad
każdym punktem
 z
z
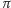 nalejemy jej tyle samo. Dla dowodu
własności (iv) ustalmy dwa punkty
nalejemy jej tyle samo. Dla dowodu
własności (iv) ustalmy dwa punkty
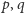 z
z
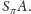 Naszym celem jest
udowodnić, że
Naszym celem jest
udowodnić, że
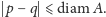 Niech
Niech
 i
i
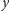 będą
odpowiednio rzutami punktów
będą
odpowiednio rzutami punktów
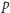 i
i
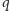 na
na
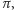 a
a
 i
i
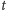 – rzutami
– rzutami
 i
i
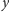 na prostą
na prostą
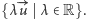 Przy tych
oznaczeniach możemy napisać
Przy tych
oznaczeniach możemy napisać

Oznaczmy jeszcze przez
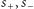 i
i
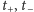 odpowiednio końce lewy
i prawy odcinków
odpowiednio końce lewy
i prawy odcinków
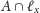 i
i
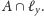 Mamy wtedy
Mamy wtedy
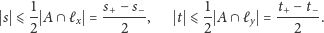
Stąd
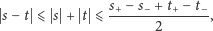
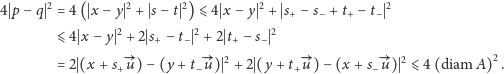
Dla jeszcze większego oswojenia się z naszym narzędziem dobrym ćwiczeniem, drogi Czytelniku, jest samodzielne udowodnienie własności (i).
Przyszła teraz pora na rozumowanie finałowe, jeśli chodzi o odpowiedź na
Pytanie 1. Mając dowolną wypukłą bryłę
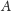 o średnicy
o średnicy
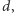 wysymetryzujmy ją kolejno względem każdej z trzech płaszczyzn
wysymetryzujmy ją kolejno względem każdej z trzech płaszczyzn
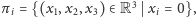
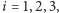 wyznaczonych przez
wszystkie możliwe pary osi
wyznaczonych przez
wszystkie możliwe pary osi
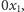
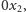
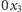 układu
współrzędnych. W ten sposób powstaje bryła
układu
współrzędnych. W ten sposób powstaje bryła
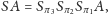 która
jako symetryczna względem każdej z płaszczyzn
która
jako symetryczna względem każdej z płaszczyzn
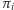 jest środkowo
symetryczna względem zera. Zatem dla dowolnego punktu
jest środkowo
symetryczna względem zera. Zatem dla dowolnego punktu
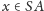 jest też
jest też
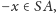 więc
więc

co oznacza, że bryła
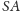 jest zawarta w kuli
jest zawarta w kuli
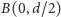 o środku
w zerze i promieniu
o środku
w zerze i promieniu
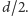 Stąd
Stąd
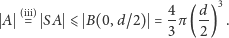 | (D) |
Uzyskaliśmy tym samym (D) – tak zwaną nierówność izodiametryczną.
Wynika z niej, że wśród ciał o ustalonej średnicy
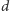 największą
objętość ma kula o promieniu
największą
objętość ma kula o promieniu
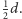 Jest to odpowiedź na postawione na
początku Pytanie 1. Trudne?
Jest to odpowiedź na postawione na
początku Pytanie 1. Trudne?
Przypomnijmy sobie, że zaczęliśmy od badania średnicy bryły wypukłej. Inną
wielkością charakteryzującą to, jak duża może być bryła, jest z pewnością
pole powierzchni
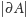 jej brzegu
jej brzegu
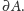 W duchu poprzedniego
pytania można się też zastanawiać, czy ma to jakiś związek z objętością
bryły, i zadać kolejne pytanie.
W duchu poprzedniego
pytania można się też zastanawiać, czy ma to jakiś związek z objętością
bryły, i zadać kolejne pytanie.
Pytanie 2. Które spośród wszystkich
brył wypukłych
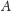 o ustalonym polu powierzchni brzegu
o ustalonym polu powierzchni brzegu
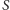 mają
największą objętość i ile ona wynosi?
mają
największą objętość i ile ona wynosi?
Jest to tzw. problem izoperymetryczny, wiązany w mitologii rzymskiej z imieniem Dydony, pierwszej królowej Kartaginy. Ścisłego rozwiązania doczekał się on jednak dopiero w XIX w. Nasz bohater, Jakub Steiner, przy użyciu swojej symetryzacji rozwiązał go na płaszczyźnie w 1838 roku. Naszkicujemy teraz jego argument. Na początku kluczowe jest zauważenie kolejnej własności symetryzacji Steinera:
- (v)
- nie powiększa pola powierzchni brzegu –
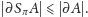
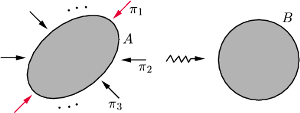
Rys. 4 Twierdzenie o kuli śnieżnej.
Dalej już wystarczy tylko wiedzieć, że startując z dowolnej bryły wypukłej
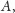 można znaleźć taki ciąg płaszczyzn
można znaleźć taki ciąg płaszczyzn
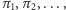 że
symetryzując
że
symetryzując
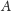 kolejno względem nich będziemy w pewnym sensie coraz
bliżej pewnej kuli
kolejno względem nich będziemy w pewnym sensie coraz
bliżej pewnej kuli
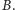 Nazwa tego twierdzenia doskonale prezentuje jego
ideę. Jest to tzw. twierdzenie o kuli śnieżnej.
Nazwa tego twierdzenia doskonale prezentuje jego
ideę. Jest to tzw. twierdzenie o kuli śnieżnej.
Zatem
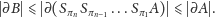
Ale symetryzacja nie zmienia objętości (pamiętamy o własności (iii)), więc
kula
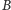 ma taką objętość jak bryła
ma taką objętość jak bryła
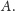 Czyli
Czyli
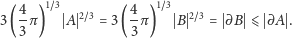 | (P) |
Otrzymaliśmy tym samym klasyczną nierówność izoperymetryczną. Znowu widać, że kule są ekstremalne — przy ustalonym polu powierzchni mają największą objętość.
Widzimy, że zupełnie elementarnie byliśmy w stanie odpowiedzieć na dwa wariacyjne pytania. Wszystko dzięki prostej geometrycznej idei symetryzacji. Do kompletności wywodu pozostał dowód twierdzenia o kuli śnieżnej i faktu, że symetryzacja nie powiększa pola powierzchni, ale to już temat na inną opowieść.
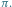
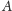 nazywamy wypukłą, jeśli wraz z każdymi dwoma swoimi
punktami zawiera odcinek łączący te punkty.
nazywamy wypukłą, jeśli wraz z każdymi dwoma swoimi
punktami zawiera odcinek łączący te punkty.
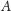 prostą
prostą
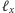 jest
wypukłym podzbiorem tej prostej, czyli odcinkiem.
jest
wypukłym podzbiorem tej prostej, czyli odcinkiem.
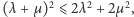 słusznej
dla dowolnych liczb rzeczywistych
słusznej
dla dowolnych liczb rzeczywistych
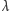 i
i
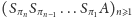 zbiega w metryce Hausdorffa do pewnej kuli
zbiega w metryce Hausdorffa do pewnej kuli