Z orbity na orbitę
Wyobraźmy sobie wahadłowiec krążący wokół Ziemi po kołowej orbicie o promieniu 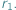 Jego prędkość w tym ruchu
Jego prędkość w tym ruchu 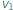 można łatwo wyznaczyć, biorąc pod uwagę, że siła grawitacji pełni rolę siły dośrodkowej, zakrzywiającej tor lotu wahadłowca...
można łatwo wyznaczyć, biorąc pod uwagę, że siła grawitacji pełni rolę siły dośrodkowej, zakrzywiającej tor lotu wahadłowca...
Można to ująć równaniem
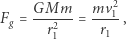 |
gdzie 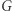 jest stałą grawitacji,
jest stałą grawitacji, 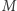 masą Ziemi, a
masą Ziemi, a 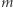 masą wahadłowca. Wynika z tego, że
masą wahadłowca. Wynika z tego, że
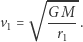 |
Załóżmy, że misja wahadłowca wymaga przejścia na inną kołową orbitę o większym promieniu 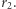 Wzór analogiczny do powyższego przewiduje, że prędkość na tej nowej, większej orbicie będzie mniejsza:
Wzór analogiczny do powyższego przewiduje, że prędkość na tej nowej, większej orbicie będzie mniejsza:
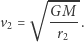 |
Tymczasem, aby osiągnąć tę orbitę, wahadłowiec musi nie przyhamować, lecz zwiększyć prędkość ponad wartość 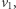 co może wydać się dziwne.
co może wydać się dziwne.
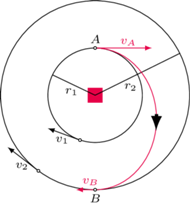
rys1. Przejście z orbity o promieniu  na orbitę o promieniu
na orbitę o promieniu 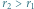 z zastosowaniem manewru Hohmanna
z zastosowaniem manewru Hohmanna
Poniżej opisane są dwa sposoby przeprowadzenia takiej zmiany orbity.
Pierwszy z nich znany jest jako manewr transferowy Hohmanna. Nazwa ta pochodzi od nazwiska Waltera Hohmanna, niemieckiego naukowca, który opisał go w roku 1925. Zmiana orbity składa się z kilku etapów przedstawionych na rysunku 1. W pewnym punkcie 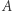 orbity kołowej ciąg silników wahadłowca - zakładamy dla uproszczenia, że działają bardzo krótko - nadaje mu prędkość
orbity kołowej ciąg silników wahadłowca - zakładamy dla uproszczenia, że działają bardzo krótko - nadaje mu prędkość
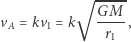 |
gdzie 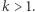 Powoduje to zmianę kształtu orbity z okręgu w elipsę, której ognisko pokrywa się ze środkiem Ziemi. (Zakładamy, że intencją kosmonautów nie jest ucieczka w kosmos po paraboli lub hiperboli, więc
Powoduje to zmianę kształtu orbity z okręgu w elipsę, której ognisko pokrywa się ze środkiem Ziemi. (Zakładamy, że intencją kosmonautów nie jest ucieczka w kosmos po paraboli lub hiperboli, więc 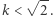 ) Prędkość
) Prędkość 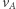 powinna być tak dobrana, aby apogeum elipsy, tj. punkt
powinna być tak dobrana, aby apogeum elipsy, tj. punkt 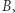 znalazło się na planowanej orbicie kołowej. Zasada zachowania momentu pędu dla ruchu po tej elipsie wyraża się równością
znalazło się na planowanej orbicie kołowej. Zasada zachowania momentu pędu dla ruchu po tej elipsie wyraża się równością
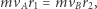 |
więc w punkcie 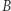 wahadłowiec będzie miał prędkość
wahadłowiec będzie miał prędkość
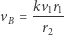 |
mniejszą od 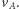 Czynnik
Czynnik 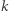 określający wartość
określający wartość 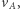 a także prędkość
a także prędkość 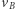 można wyznaczyć z zasady zachowania energii zapisanej dla ruchu po elipsie. Zachowanie energii oznacza równość całkowitych energii w perigeum (punkt
można wyznaczyć z zasady zachowania energii zapisanej dla ruchu po elipsie. Zachowanie energii oznacza równość całkowitych energii w perigeum (punkt 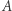 ) i apogeum (punkt
) i apogeum (punkt  )
)
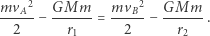 |
Stąd otrzymujemy
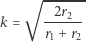 |
oraz
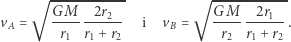 |
Prędkość 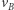 jest mniejsza od
jest mniejsza od 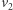 odpowiadającej orbicie kołowej przechodzącej przez punkt
odpowiadającej orbicie kołowej przechodzącej przez punkt 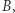 dlatego aby przejść z orbity eliptycznej na kołową, wahadłowiec musi drugi raz przyspieszyć. Pierwsze przyspieszenie jest niezbędne, aby zastąpić kołową orbitę elipsą z apogeum w odległości
dlatego aby przejść z orbity eliptycznej na kołową, wahadłowiec musi drugi raz przyspieszyć. Pierwsze przyspieszenie jest niezbędne, aby zastąpić kołową orbitę elipsą z apogeum w odległości 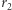 od środka Ziemi, gdzie energia potencjalna jest większa niż w odległości
od środka Ziemi, gdzie energia potencjalna jest większa niż w odległości 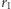 i trzeba ją uzyskać kosztem energii kinetycznej zwiększonej przyspieszającym działaniem silników. Drugie przyspieszenie jest konieczne, aby odrobić stratę prędkości powstałą podczas ruchu po elipsie od
i trzeba ją uzyskać kosztem energii kinetycznej zwiększonej przyspieszającym działaniem silników. Drugie przyspieszenie jest konieczne, aby odrobić stratę prędkości powstałą podczas ruchu po elipsie od 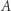 do
do 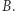 Wartości bezwzględne zmian prędkości wynoszą
Wartości bezwzględne zmian prędkości wynoszą
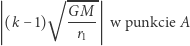 |
oraz
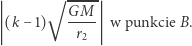 |
Suma ich modułów bywa używana jako miara wydatku energii niezbędnej do wykonania manewru, uzyskanej kosztem zużycia paliwa przez silniki. Czas przejścia, czyli czas lotu po połówce elipsy, można obliczyć ze wzoru
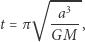 |
gdzie 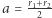 jest długością dużej półosi elipsy. Wzór ten wyraża połowę ujętego III prawem Keplera okresu obiegu po pełnej eliptycznej orbicie. Analogiczne rozważania dotyczą przejścia z orbity dalszej na bliższą Ziemi. Po przyhamowaniu następuje lot po trajektorii eliptycznej, która zbliża wahadłowiec do Ziemi. Druga redukcja prędkości zapewnia prędkość właściwą dla ruchu po planowanej orbicie kołowej.
jest długością dużej półosi elipsy. Wzór ten wyraża połowę ujętego III prawem Keplera okresu obiegu po pełnej eliptycznej orbicie. Analogiczne rozważania dotyczą przejścia z orbity dalszej na bliższą Ziemi. Po przyhamowaniu następuje lot po trajektorii eliptycznej, która zbliża wahadłowiec do Ziemi. Druga redukcja prędkości zapewnia prędkość właściwą dla ruchu po planowanej orbicie kołowej.

Rys. 2 Przejście z orbity o promieniu  na orbitę o promieniu
na orbitę o promieniu 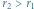 z zastosowaniem transferu dwueliptycznego
z zastosowaniem transferu dwueliptycznego
Dla przykładu rozważmy przejście z orbity o promieniu 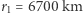 na
na 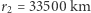 . Następowałoby ono dzięki przyspieszeniom od
. Następowałoby ono dzięki przyspieszeniom od 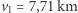 /s do
/s do 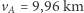 /s oraz od
/s oraz od 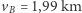 /s do
/s do 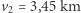 /s. Suma zmian prędkości wynosiłaby
/s. Suma zmian prędkości wynosiłaby 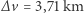 /s, a cały manewr trwałby 3 godziny i 56 minut.
/s, a cały manewr trwałby 3 godziny i 56 minut.
Manewr Hohmanna przestaje być optymalny przy dużym stosunku promieni orbit 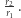 Wtedy lepiej zastosować tzw. transfer dwueliptyczny, służący także do zmiany orbity mniejszej na większą i odwrotnie. Przejście z niskiej orbity o promieniu
Wtedy lepiej zastosować tzw. transfer dwueliptyczny, służący także do zmiany orbity mniejszej na większą i odwrotnie. Przejście z niskiej orbity o promieniu 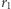 na wyższą o promieniu
na wyższą o promieniu 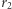 zilustrowane jest na rysunku 2.
zilustrowane jest na rysunku 2.
Tak jak w manewrze Hohmanna, krótki impuls ciągu w punkcie 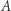 pierwotnej orbity zwiększa prędkość od
pierwotnej orbity zwiększa prędkość od 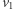 do
do 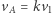 (gdzie
(gdzie 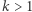 ), dzięki czemu wahadłowiec wchodzi na orbitę eliptyczną. Jej kształt określony jest odległością
), dzięki czemu wahadłowiec wchodzi na orbitę eliptyczną. Jej kształt określony jest odległością 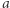 od ogniska (środek Ziemi) do apogeum (punkt
od ogniska (środek Ziemi) do apogeum (punkt 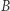 ). Wielkość
). Wielkość 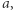 która musi być większa od
która musi być większa od 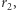 powinna być wybrana z uwzględnieniem faktu, że decyduje o energii zużytej na wykonanie transferu i o czasie jego trwania. Podczas lotu po połowie elipsy od
powinna być wybrana z uwzględnieniem faktu, że decyduje o energii zużytej na wykonanie transferu i o czasie jego trwania. Podczas lotu po połowie elipsy od 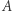 do
do 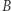 prędkość w punkcie
prędkość w punkcie 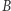 spada do wartości
spada do wartości 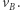 W tym punkcie następuje kolejne impulsowe przyspieszenie do prędkości
W tym punkcie następuje kolejne impulsowe przyspieszenie do prędkości 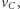 dobranej tak, aby wahadłowiec kontynuował lot po innej eliptycznej orbicie z apogeum w punkcie
dobranej tak, aby wahadłowiec kontynuował lot po innej eliptycznej orbicie z apogeum w punkcie 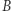 i perigeum w punkcie
i perigeum w punkcie 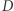 leżącym już na orbicie końcowej. Dążąc po tej elipsie do perigeum, wahadłowiec przyspiesza i do punktu
leżącym już na orbicie końcowej. Dążąc po tej elipsie do perigeum, wahadłowiec przyspiesza i do punktu 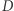 dociera z prędkością
dociera z prędkością 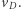 Jest ona większa niż
Jest ona większa niż 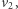 a więc do przejścia na orbitę kołową o promieniu
a więc do przejścia na orbitę kołową o promieniu 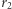 niezbędne jest hamowanie od
niezbędne jest hamowanie od 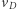 do
do 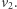 Wzory wyrażające zasady zachowania pozwalają obliczyć poszczególne prędkości.
Wzory wyrażające zasady zachowania pozwalają obliczyć poszczególne prędkości.
Jeśli zmiana orbity z 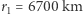 na
na 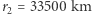 odbyłaby się drogą transferu dwueliptycznego z parametrem równym np. 50
odbyłaby się drogą transferu dwueliptycznego z parametrem równym np. 50 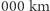 , to charakterystyczne prędkości wynosiłyby
, to charakterystyczne prędkości wynosiłyby 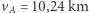 /s
/s 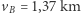 /s,
/s, 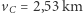 /s i
/s i 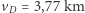 /s. Sumaryczna zmiana prędkości
/s. Sumaryczna zmiana prędkości 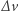 przyjęłaby wartość 4,
przyjęłaby wartość 4, 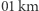 /s, co oznacza większe zużycie paliwa niż podczas transferu Hohmanna. Zmiana orbity zajęłaby także dużo więcej czasu, bo aż 44 godziny i 52 minuty. Ten przykład ilustruje główną wadę transferu dwueliptycznego, jaką jest długi czas jego realizacji. Manewr dwueliptyczny przeprowadzony z dowolnym
/s, co oznacza większe zużycie paliwa niż podczas transferu Hohmanna. Zmiana orbity zajęłaby także dużo więcej czasu, bo aż 44 godziny i 52 minuty. Ten przykład ilustruje główną wadę transferu dwueliptycznego, jaką jest długi czas jego realizacji. Manewr dwueliptyczny przeprowadzony z dowolnym 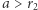 jest oszczędniejszy od manewru Hohmanna, jeśli
jest oszczędniejszy od manewru Hohmanna, jeśli 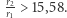 Taką samą przewagę ma on, gdy
Taką samą przewagę ma on, gdy 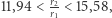 pod warunkiem, że przeprowadza się go z dostatecznie dużą wartością
pod warunkiem, że przeprowadza się go z dostatecznie dużą wartością 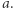 Natomiast gdy
Natomiast gdy 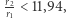 to żaden wariant transferu dwueliptycznego nie jest korzystniejszy od manewru Hohmanna. Różnice w zużyciu paliwa pomiędzy tymi dwiema procedurami są jednak niewielkie. Maksymalna oszczędność, jaką można uzyskać, zastępując manewr Hohmanna dwueliptycznym, wynosi 8%.
to żaden wariant transferu dwueliptycznego nie jest korzystniejszy od manewru Hohmanna. Różnice w zużyciu paliwa pomiędzy tymi dwiema procedurami są jednak niewielkie. Maksymalna oszczędność, jaką można uzyskać, zastępując manewr Hohmanna dwueliptycznym, wynosi 8%.
 na orbitę o promieniu
na orbitę o promieniu 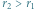 z zastosowaniem manewru Hohmanna
z zastosowaniem manewru Hohmanna na orbitę o promieniu
na orbitę o promieniu 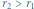 z zastosowaniem transferu dwueliptycznego
z zastosowaniem transferu dwueliptycznego