W chwili początkowej prędkość względna powierzchni kółek w punkcie ich styku wynosiła 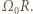 Na powierzchnie kółek działały więc siły tarcia kinetycznego równe co do wielkości, ale skierowane przeciwnie. Większe kółko było "hamowane", a mniejsze "przyspieszane", aż do chwili, gdy prędkości liniowe powierzchni w miejscu ich styku wyrównały się, co oznacza, że końcowe prędkości kątowe większego kółka
Na powierzchnie kółek działały więc siły tarcia kinetycznego równe co do wielkości, ale skierowane przeciwnie. Większe kółko było "hamowane", a mniejsze "przyspieszane", aż do chwili, gdy prędkości liniowe powierzchni w miejscu ich styku wyrównały się, co oznacza, że końcowe prędkości kątowe większego kółka 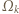 i mniejszego
i mniejszego 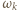 spełniły warunek:
spełniły warunek:

(znak minus, bo obroty są w przeciwne strony). Niech 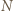 oznacza siłę dociskającą powierzchnie kółek,
oznacza siłę dociskającą powierzchnie kółek, 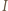 moment bezwładności większego z nich, a
moment bezwładności większego z nich, a 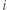 mniejszego. Mamy równania ruchu obrotowego walców:
mniejszego. Mamy równania ruchu obrotowego walców:
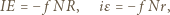
gdzie 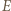 i
i  oznaczają odpowiednio przyspieszenia kątowe większego i mniejszego kółka (w obu równaniach występuje po prawej stronie znak minus, bo i siły, i wektory położenia punktów przyłożenia sił względem osi kółek są skierowane przeciwnie). Z upływem czasu
oznaczają odpowiednio przyspieszenia kątowe większego i mniejszego kółka (w obu równaniach występuje po prawej stronie znak minus, bo i siły, i wektory położenia punktów przyłożenia sił względem osi kółek są skierowane przeciwnie). Z upływem czasu 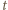 prędkość kątowa większego kółka
prędkość kątowa większego kółka 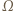 zmienia się jak
zmienia się jak 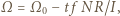 a mniejszego jak
a mniejszego jak 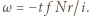 Podstawienie tych zależności do warunku
Podstawienie tych zależności do warunku 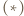 pozwala znaleźć czas ruchu
pozwala znaleźć czas ruchu 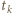 do chwili ustania poślizgu powierzchni:
do chwili ustania poślizgu powierzchni:
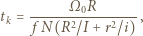
a następnie końcową prędkość kątową 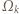 :
:
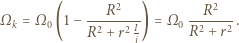
Ostatnia równość wynika z faktu, że jeśli kółka wycięto z tego samego arkusza blachy, to ich masy pozostają w stosunku jak kwadraty ich promieni, a momenty bezwładności jak czwarte potęgi promieni. Jak widać, siła tarcia 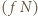 występuje tylko we wzorze na
występuje tylko we wzorze na 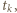 co oznacza, że tę samą wartość
co oznacza, że tę samą wartość 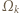 otrzymalibyśmy, gdyby uzgodnienie prędkości obrotu następowało natychmiast po zetknięciu kółek, tak jak można by przyjąć dla kół zębatych.
otrzymalibyśmy, gdyby uzgodnienie prędkości obrotu następowało natychmiast po zetknięciu kółek, tak jak można by przyjąć dla kół zębatych.
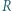 i
i 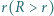 wycięte z tego samego arkusza blachy osadzone są na dwóch równoległych osiach, wokół których mogą się swobodnie obracać. Większe z kółek wprawiono w ruch obrotowy, nadając mu prędkość kątową
wycięte z tego samego arkusza blachy osadzone są na dwóch równoległych osiach, wokół których mogą się swobodnie obracać. Większe z kółek wprawiono w ruch obrotowy, nadając mu prędkość kątową 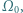 a następnie osie zsunięto tak, że kółka stykały się. Jaka ustaliła się końcowa prędkość kątowa większego z kółek? Przyjmij, że współczynnik tarcia kinetycznego między powierzchniami bocznymi kółek wynosi
a następnie osie zsunięto tak, że kółka stykały się. Jaka ustaliła się końcowa prędkość kątowa większego z kółek? Przyjmij, że współczynnik tarcia kinetycznego między powierzchniami bocznymi kółek wynosi 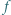 i pomiń pozostałe opory ruchu (tarcie w zamocowaniu osi, opór powietrza itp.).
i pomiń pozostałe opory ruchu (tarcie w zamocowaniu osi, opór powietrza itp.).
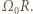 Na powierzchnie kółek działały więc siły tarcia kinetycznego równe co do wielkości, ale skierowane przeciwnie. Większe kółko było "hamowane", a mniejsze "przyspieszane", aż do chwili, gdy prędkości liniowe powierzchni w miejscu ich styku wyrównały się, co oznacza, że końcowe prędkości kątowe większego kółka
Na powierzchnie kółek działały więc siły tarcia kinetycznego równe co do wielkości, ale skierowane przeciwnie. Większe kółko było "hamowane", a mniejsze "przyspieszane", aż do chwili, gdy prędkości liniowe powierzchni w miejscu ich styku wyrównały się, co oznacza, że końcowe prędkości kątowe większego kółka 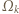 i mniejszego
i mniejszego 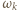 spełniły warunek:
spełniły warunek:
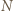 oznacza siłę dociskającą powierzchnie kółek,
oznacza siłę dociskającą powierzchnie kółek, 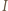 moment bezwładności większego z nich, a
moment bezwładności większego z nich, a 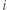 mniejszego. Mamy równania ruchu obrotowego walców:
mniejszego. Mamy równania ruchu obrotowego walców: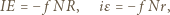
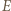 i
i  oznaczają odpowiednio przyspieszenia kątowe większego i mniejszego kółka (w obu równaniach występuje po prawej stronie znak minus, bo i siły, i wektory położenia punktów przyłożenia sił względem osi kółek są skierowane przeciwnie). Z upływem czasu
oznaczają odpowiednio przyspieszenia kątowe większego i mniejszego kółka (w obu równaniach występuje po prawej stronie znak minus, bo i siły, i wektory położenia punktów przyłożenia sił względem osi kółek są skierowane przeciwnie). Z upływem czasu 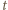 prędkość kątowa większego kółka
prędkość kątowa większego kółka 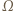 zmienia się jak
zmienia się jak 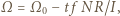 a mniejszego jak
a mniejszego jak 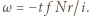 Podstawienie tych zależności do warunku
Podstawienie tych zależności do warunku 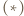 pozwala znaleźć czas ruchu
pozwala znaleźć czas ruchu 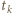 do chwili ustania poślizgu powierzchni:
do chwili ustania poślizgu powierzchni: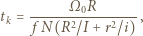
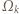 :
: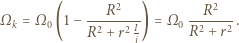
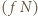 występuje tylko we wzorze na
występuje tylko we wzorze na 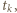 co oznacza, że tę samą wartość
co oznacza, że tę samą wartość 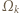 otrzymalibyśmy, gdyby uzgodnienie prędkości obrotu następowało natychmiast po zetknięciu kółek, tak jak można by przyjąć dla kół zębatych.
otrzymalibyśmy, gdyby uzgodnienie prędkości obrotu następowało natychmiast po zetknięciu kółek, tak jak można by przyjąć dla kół zębatych.