Klub 44F - zadania I 2017»Zadanie 631
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2017
- Publikacja w Delcie: styczeń 2017
- Publikacja elektroniczna: 30 grudnia 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (78 KB)
Na powierzchni poziomej znajdują się dwa jednakowe, cienkościenne walce o masie  każdy. Osie walców są równoległe, promienie są równe
każdy. Osie walców są równoległe, promienie są równe 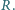 Na początku jeden z walców spoczywa, a drugi toczy się bez poślizgu w kierunku pierwszego z prędkością ruchu postępowego
Na początku jeden z walców spoczywa, a drugi toczy się bez poślizgu w kierunku pierwszego z prędkością ruchu postępowego 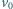 aż do centralnego, sprężystego zderzenia. Współczynnik tarcia kinetycznego walców o podłoże jest równy
aż do centralnego, sprężystego zderzenia. Współczynnik tarcia kinetycznego walców o podłoże jest równy 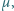 tarcie między walcami jest zaniedbywalne. Znaleźć maksymalną odległość między walcami po zderzeniu.
tarcie między walcami jest zaniedbywalne. Znaleźć maksymalną odległość między walcami po zderzeniu.

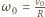 nie zmienia się w wyniku zderzenia. Z zasad zachowania pędu i energii (zderzenie sprężyste) wynika, że po zderzeniu prędkość ruchu postępowego pierwszego walca wynosi zero, a drugiego
nie zmienia się w wyniku zderzenia. Z zasad zachowania pędu i energii (zderzenie sprężyste) wynika, że po zderzeniu prędkość ruchu postępowego pierwszego walca wynosi zero, a drugiego 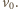 Po zderzeniu na pierwszy walec działa siła tarcia skierowana do przodu. Jego prędkość ruchu postępowego rośnie liniowo z czasem:
Po zderzeniu na pierwszy walec działa siła tarcia skierowana do przodu. Jego prędkość ruchu postępowego rośnie liniowo z czasem: 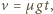 prędkość kątowa ruchu obrotowego maleje liniowo z czasem:
prędkość kątowa ruchu obrotowego maleje liniowo z czasem: 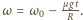 Po czasie
Po czasie 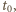 gdy spełniony jest związek
gdy spełniony jest związek 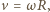 rozpoczyna się toczenie bez poślizgu. Stąd
rozpoczyna się toczenie bez poślizgu. Stąd 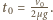 Na drugi walec działa siła tarcia skierowana do tyłu. Jego prędkość ruchu postępowego maleje liniowo z czasem, prędkość ruchu obrotowego rośnie liniowo z czasem. Po czasie
Na drugi walec działa siła tarcia skierowana do tyłu. Jego prędkość ruchu postępowego maleje liniowo z czasem, prędkość ruchu obrotowego rośnie liniowo z czasem. Po czasie 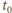 drugi walec również zaczyna toczyć się bez poślizgu. Od chwili
drugi walec również zaczyna toczyć się bez poślizgu. Od chwili 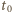 prędkości ruchu postępowego obu walców wynoszą
prędkości ruchu postępowego obu walców wynoszą 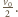 Drogi przebyte przez walce w czasie
Drogi przebyte przez walce w czasie 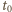 wynoszą odpowiednio
wynoszą odpowiednio 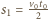 i
i 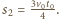 Maksymalna odległość, na jaką się oddalą, jest równa
Maksymalna odległość, na jaką się oddalą, jest równa