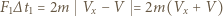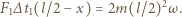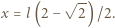Klub 44F - zadania XI 2019»Zadanie 686
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania XI 2019
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (376 KB)

Dwie małe kulki o masach 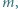 połączone nieważkim prętem o długości
połączone nieważkim prętem o długości 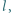 spoczywają na gładkim stole. W odległości
spoczywają na gładkim stole. W odległości  od jednej z kulek znajduje się wbity w powierzchnię stołu kołek. W chwili początkowej odległość między prętem a kołkiem jest bardzo mała (rysunek). Kulka położona bliżej kołka została uderzona w kierunku równoległym do powierzchni stołu i prostopadłym do pręta i w bardzo krótkim czasie uzyskała prędkość
od jednej z kulek znajduje się wbity w powierzchnię stołu kołek. W chwili początkowej odległość między prętem a kołkiem jest bardzo mała (rysunek). Kulka położona bliżej kołka została uderzona w kierunku równoległym do powierzchni stołu i prostopadłym do pręta i w bardzo krótkim czasie uzyskała prędkość 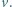 Następnie pręt zderzył się sprężyście z kołkiem. Jaka powinna być odległość
Następnie pręt zderzył się sprężyście z kołkiem. Jaka powinna być odległość 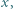 aby po zderzeniu pręt nie obracał się?
aby po zderzeniu pręt nie obracał się?

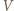 opisuje równanie
opisuje równanie 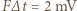 , gdzie
, gdzie 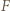 jest średnią siłą działającą na kulkę w czasie zderzenia
jest średnią siłą działającą na kulkę w czasie zderzenia 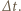 Równanie ruchu obrotowego układu z prędkością kątową
Równanie ruchu obrotowego układu z prędkością kątową 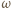 wokół środka masy ma postać
wokół środka masy ma postać 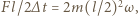 stąd
stąd 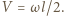 Ruch kulki, której nadano prędkość
Ruch kulki, której nadano prędkość 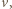 jest złożeniem ruchu postępowego i obrotowego, zatem
jest złożeniem ruchu postępowego i obrotowego, zatem 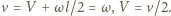 Prędkość drugiej kulki wynosi
Prędkość drugiej kulki wynosi 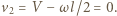 Po zderzeniu sprężystym z kołkiem ruch układu jest ruchem czysto postępowym, zasada zachowania energii ma więc postać
Po zderzeniu sprężystym z kołkiem ruch układu jest ruchem czysto postępowym, zasada zachowania energii ma więc postać 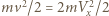 , gdzie
, gdzie 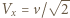 jest prędkością układu po zderzeniu. Oznaczając przez
jest prędkością układu po zderzeniu. Oznaczając przez 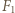 średnią siłę działającą na pręt w czasie
średnią siłę działającą na pręt w czasie 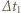 podczas zderzenia z kołkiem, możemy napisać równanie ruchu postępowego:
podczas zderzenia z kołkiem, możemy napisać równanie ruchu postępowego: