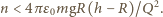Każda kropla, wpadając do naczynia, powiększa jego ładunek o 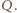Ładunek ten rozkłada się równomiernie na powierzchni sfery i wytwarza wokół niej pole elektryczne, które jest takie jak pole pochodzące od ładunku punktowego, równego ładunkowi sfery, umieszczonego w jej środku. Na spadającą kroplę działają więc dwie siły: przyspieszająca ruch kropli siła ciężkości i opóźniająca ten ruch siła elektrostatyczna. Przyjmijmy, że do naczynia wpadło kropli, a więc jego ładunek wynosi 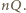Kropla 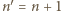już do naczynia nie wpadnie, jeżeli jej prędkość na wysokości otworu w naczyniu będzie równa zeru.

Prędkość tę znajdziemy, obliczając energię kinetyczną, jaką ma na wysokości 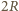kropla spadająca z wysokości 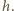Będzie ona równa zmianie jej energii potencjalnej, na którą składa się energia pochodząca od pola grawitacyjnego i od pola elektrycznego przy spadku z wysokości 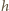do wysokości :

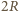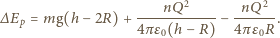
Mamy więc

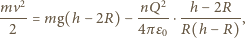
a stąd

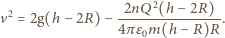
Z warunku 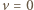dostajemy

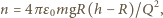
a to oznacza, że ostatnia kropla, która wpadnie do naczynia, ma numer 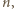będący największą liczbą całkowitą spełniającą warunek: