Klub 44F - zadania I 2015»Zadanie 590
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2015
- Publikacja w Delcie: styczeń 2015
- Publikacja elektroniczna: 1 stycznia 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (93 KB)
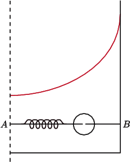
W naczyniu w kształcie walca znajduje się ciecz o gęstości 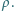 Walec obraca się ze stałą prędkością kątową
Walec obraca się ze stałą prędkością kątową 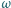 wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt
wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt 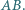 Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie
Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie  i promieniu
i promieniu 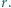 Kula połączona jest z końcem
Kula połączona jest z końcem 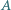 pręta za pomocą sprężyny o współczynniku sprężystości
pręta za pomocą sprężyny o współczynniku sprężystości 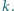 Długość nieodkształconej sprężyny wynosi
Długość nieodkształconej sprężyny wynosi 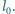 Znaleźć odległość środka kuli od osi obrotu.
Znaleźć odległość środka kuli od osi obrotu.

 szukaną odległość środka kuli od punktu
szukaną odległość środka kuli od punktu 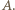 W układzie inercjalnym w kierunku wzdłuż pręta działają na kulę: siła sprężystości
W układzie inercjalnym w kierunku wzdłuż pręta działają na kulę: siła sprężystości 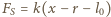 oraz siła ze strony cieczy
oraz siła ze strony cieczy 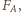 a ich wypadkowa jest siłą dośrodkową
a ich wypadkowa jest siłą dośrodkową 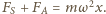 Aby wyznaczyć siłę
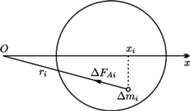
Aby wyznaczyć siłę 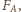 rozważmy obracające się naczynie z samą cieczą, wyodrębnijmy w niej myślowo część znajdującą się w tym samym miejscu co kula i podzielmy ją na bardzo małe elementy o masach
rozważmy obracające się naczynie z samą cieczą, wyodrębnijmy w niej myślowo część znajdującą się w tym samym miejscu co kula i podzielmy ją na bardzo małe elementy o masach 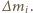 Siła ze strony pozostałej cieczy działająca na taki element w płaszczyźnie poziomej wynosi
Siła ze strony pozostałej cieczy działająca na taki element w płaszczyźnie poziomej wynosi 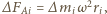 gdzie
gdzie 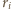 jest odległością elementu od osi obrotu. Niech pozioma oś
jest odległością elementu od osi obrotu. Niech pozioma oś 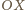 prostokątnego układu współrzędnych ma początek na osi obrotu i przechodzi przez środek wydzielonej części cieczy, a oś
prostokątnego układu współrzędnych ma początek na osi obrotu i przechodzi przez środek wydzielonej części cieczy, a oś 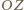 skierowana jest wzdłuż osi obrotu, prostopadle do płaszczyzny rysunku. Rzut siły
skierowana jest wzdłuż osi obrotu, prostopadle do płaszczyzny rysunku. Rzut siły 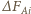 na oś
na oś 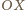 wynosi
wynosi 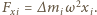 Całkowita siła działająca w płaszczyźnie poziomej ze strony pozostałej cieczy na część wyróżnioną działa wzdłuż osi
Całkowita siła działająca w płaszczyźnie poziomej ze strony pozostałej cieczy na część wyróżnioną działa wzdłuż osi 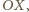 co wynika z symetrii problemu, skierowana jest do osi obrotu i ma wartość
co wynika z symetrii problemu, skierowana jest do osi obrotu i ma wartość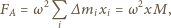
 jest odległością środka masy kuli od osi obrotu, a
jest odległością środka masy kuli od osi obrotu, a 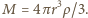 Siła
Siła 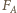 zależy tylko od położenia, kształtu i objętości wyróżnionej części cieczy. Taka sama siła działa na dowolne ciało umieszczone w tym samym miejscu wewnątrz cieczy. Szukana odległość wynosi
zależy tylko od położenia, kształtu i objętości wyróżnionej części cieczy. Taka sama siła działa na dowolne ciało umieszczone w tym samym miejscu wewnątrz cieczy. Szukana odległość wynosi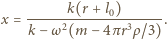
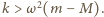 W przeciwnym przypadku sprężyna jest zbyt słaba, aby utrzymać kulę wewnątrz cieczy, i kula w zależności od swojej gęstości przemieszcza się do jednego z końców pręta.
W przeciwnym przypadku sprężyna jest zbyt słaba, aby utrzymać kulę wewnątrz cieczy, i kula w zależności od swojej gęstości przemieszcza się do jednego z końców pręta.