Klub 44F - zadania IV 2014»Zadanie 576
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IV 2014
- Publikacja w Delcie: kwiecień 2014
- Publikacja elektroniczna: 31 marca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (232 KB)
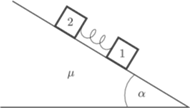
Z równi pochyłej nachylonej do poziomu pod kątem
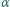 zsuwają się dwa
klocki o jednakowych masach
zsuwają się dwa
klocki o jednakowych masach
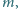 połączone nieważką sprężyną
o współczynniku sprężystości
połączone nieważką sprężyną
o współczynniku sprężystości
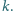 W chwili początkowej sprężyna jest
nieodkształcona, a prędkości klocków są równe zeru. Współczynnik
tarcia między drugim klockiem a równią wynosi
W chwili początkowej sprężyna jest
nieodkształcona, a prędkości klocków są równe zeru. Współczynnik
tarcia między drugim klockiem a równią wynosi
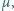 przy czym
przy czym
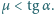 Między pierwszym klockiem a równią tarcia nie ma. Znaleźć
maksymalne wydłużenie sprężyny oraz inne wielkości charakteryzujące ruch
klocków.
Między pierwszym klockiem a równią tarcia nie ma. Znaleźć
maksymalne wydłużenie sprężyny oraz inne wielkości charakteryzujące ruch
klocków.

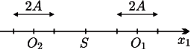
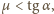 oba klocki ruszają
jednocześnie. Środek masy układu porusza się z przyspieszeniem
oba klocki ruszają
jednocześnie. Środek masy układu porusza się z przyspieszeniem
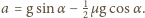 Dalej rozważać będziemy problem w układzie
środka masy.
Dalej rozważać będziemy problem w układzie
środka masy.
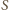 znajduje się
w połowie odległości między klockami, a ich ruch jest symetryczny względem
środka masy. Możemy więc ograniczyć się do rozpatrzenia ruchu
jednego z klocków. Wypadkowa siła, działająca na klocek pierwszy,
wynosi
znajduje się
w połowie odległości między klockami, a ich ruch jest symetryczny względem
środka masy. Możemy więc ograniczyć się do rozpatrzenia ruchu
jednego z klocków. Wypadkowa siła, działająca na klocek pierwszy,
wynosi
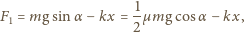
 jest odkształceniem sprężyny (
jest odkształceniem sprężyny (
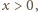 gdy sprężyna jest
rozciągnięta). Gdy
gdy sprężyna jest
rozciągnięta). Gdy
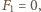 czyli w stanie równowagi, wydłużenie
sprężyny jest równe
czyli w stanie równowagi, wydłużenie
sprężyny jest równe
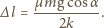
 oznacza współrzędną pierwszego klocka względem położenia
równowagi
oznacza współrzędną pierwszego klocka względem położenia
równowagi