Zadanie ZF-983
o zadaniu...
- Publikacja w Delcie: wrzesień 2019
- Publikacja elektroniczna: 1 września 2019
Dwa jednakowe, nieważkie pierścienie ślizgają się bez tarcia po pionowej, kołowej obręczy. Przez pierścienie przewleczono wiotką, nierozciągliwą i nieważką nić. Na końcach nici umocowano dwa ciężarki, każdy o masie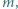 
a w jej środku ciężarek o masie 
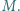W stanie równowagi pierścienie znajdują się w odległości kątowej 
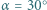od najwyższego punktu obręczy. Jaki jest stosunek mas 
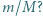Między nicią i pierścieniami nie występuje tarcie.
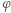oznacza kąt między pionem i odcinkami nici "trzymającymi" masę 
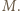Aby układ pozostawał w równowadze, siły działające na masę 
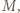masy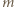 
i na każdy z pierścieni muszą się równoważyć. Nić porusza się bez tarcia wewnątrz pierścieni, a więc siła naciągu każdej z nici "trzymających" masę 
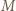równa jest ciężarowi masy 
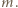Zrównoważenie ciężaru masy 
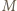wymaga spełnienia warunku: 
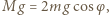a równowaga sił "ciągnących" każdy z pierścieni: 
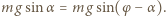Drugi z warunków, po podstawieniu wartości funkcji sinus i cosinus kąta 
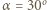oraz skorzystaniu z tożsamości 
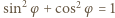prowadzi do równania 
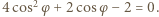Dodatnim rozwiązaniem tego równania jest 
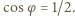Ostatecznie otrzymujemy więc 