Klub 44F - zadania X 2017»Zadanie 644
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania X 2017
- Publikacja w Delcie: październik 2017
- Publikacja elektroniczna: 29 września 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (101 KB)
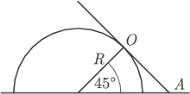
Półwalec o promieniu 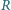 umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości
umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości 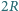 opiera się na walcu w połowie swojej długości, a jego dolny koniec
opiera się na walcu w połowie swojej długości, a jego dolny koniec 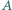 jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta
jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta 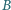 w chwili, gdy zetknie się on z powierzchnią walca?
w chwili, gdy zetknie się on z powierzchnią walca?

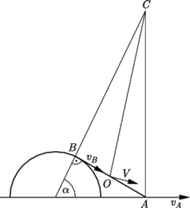
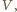 a prędkość kątową ruchu obrotowego wokół środka masy przez
a prędkość kątową ruchu obrotowego wokół środka masy przez 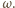 Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową
Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową 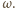 Prędkość
Prędkość 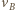 punktu
punktu 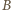 w chwili końcowej jest styczna do walca, a prędkość
w chwili końcowej jest styczna do walca, a prędkość 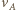 punktu
punktu 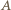 ma kierunek poziomy. Punkt
ma kierunek poziomy. Punkt 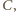 przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości
przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości 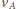 i
i 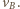 Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka
Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka 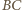 wynosi
wynosi 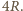 Z twierdzenia Pitagorasa długość odcinka
Z twierdzenia Pitagorasa długość odcinka 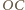 jest równa
jest równa 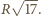 Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem
Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem 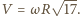 Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta
Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta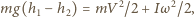
 jest masą pręta,
jest masą pręta, 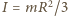 jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio
jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio 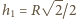 i
i 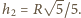 Podstawiając to do równania (1), otrzymujemy prędkość kątową
Podstawiając to do równania (1), otrzymujemy prędkość kątową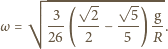
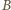 dana jest wzorem
dana jest wzorem