Klub 44F - zadania III 2015»Zadanie 594
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania III 2015
- Publikacja w Delcie: marzec 2015
- Publikacja elektroniczna: 1 marca 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (125 KB)

Żuk pełznie po sztywnej słomce, opartej o gładką podłogę i gładką pionową ściankę. Słomka jest jednorodna, tworzy z poziomem kąt 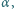 jej długość wynosi
jej długość wynosi 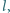 masa słomki jest zaniedbywalna w porównaniu z masą żuka
masa słomki jest zaniedbywalna w porównaniu z masą żuka  Prędkość początkowa żuka w punkcie
Prędkość początkowa żuka w punkcie 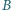 wynosi
wynosi 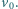 Jak musi poruszać się żuk, aby słomka pozostawała nieruchoma? Po jakim czasie dopełznie on do punktu
Jak musi poruszać się żuk, aby słomka pozostawała nieruchoma? Po jakim czasie dopełznie on do punktu 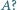

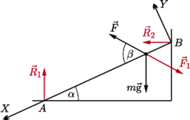
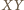 jak na rysunku obok. Niech żuk znajduje się w odległości
jak na rysunku obok. Niech żuk znajduje się w odległości 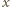 od początku układu
od początku układu 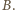 Siły działające na słomkę zaznaczono na rysunku kolorem. Są to siły reakcji
Siły działające na słomkę zaznaczono na rysunku kolorem. Są to siły reakcji 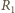 i
i 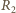 prostopadłe odpowiednio do podłogi i ścianki oraz siła
prostopadłe odpowiednio do podłogi i ścianki oraz siła 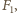 jaką żuk działa na słomkę. Siłę ciężkości działającą na słomkę pomijamy zgodnie z treścią zadania. Słomka nie porusza się, więc siły działające na nią równoważą się:
jaką żuk działa na słomkę. Siłę ciężkości działającą na słomkę pomijamy zgodnie z treścią zadania. Słomka nie porusza się, więc siły działające na nią równoważą się: 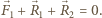 Na żuka działa siła ciężkości oraz siła reakcji słomki
Na żuka działa siła ciężkości oraz siła reakcji słomki 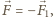 która tworzy ze słomką nieznany kąt
która tworzy ze słomką nieznany kąt 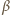 (siły te zaznaczono na rysunku na czarno). Równanie ruchu żuka ma postać
(siły te zaznaczono na rysunku na czarno). Równanie ruchu żuka ma postać 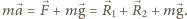 Przyspieszenie
Przyspieszenie 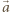 skierowane jest wzdłuż słomki. Stąd
skierowane jest wzdłuż słomki. Stąd 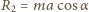 oraz
oraz 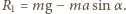 Momenty sił działających na słomkę względem dowolnego punktu równoważą się. Względem punktu
Momenty sił działających na słomkę względem dowolnego punktu równoważą się. Względem punktu 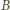 warunek ten ma postać:
warunek ten ma postać: 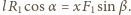 Siły działające na żuka prostopadle do słomki równoważą się:
Siły działające na żuka prostopadle do słomki równoważą się: 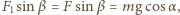 zatem
zatem 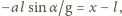 gdzie
gdzie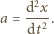
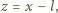 otrzymujemy równanie
otrzymujemy równanie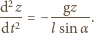
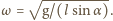 Ruch żuka opisuje funkcja
Ruch żuka opisuje funkcja 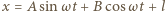 z warunkami początkowymi:
z warunkami początkowymi: 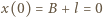 oraz
oraz 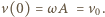 Zatem
Zatem 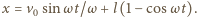 Kładąc
Kładąc 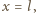 otrzymujemy czas
otrzymujemy czas 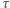 podróży żuka do końca słomki:
podróży żuka do końca słomki: