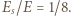Klub 44F - zadania V 2019»Zadanie 679
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania V 2019
- Publikacja w Delcie: maj 2019
- Publikacja elektroniczna: 30 kwietnia 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (373 KB)
Na gładkim lodzie zderzają się sprężyście dwa jednakowe okrągłe kamienie do gry w curling, z których jeden początkowo spoczywa, a drugi porusza się ruchem postępowym. Prosta przechodząca przez środki kamieni podczas zderzenia tworzy kąt 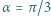 z wektorem prędkości początkowej poruszającego się kamienia. Znaleźć maksymalną część energii układu, która podczas zderzenia przechodzi w energię sprężystej deformacji. Nie ma tarcia między kamieniami.
z wektorem prędkości początkowej poruszającego się kamienia. Znaleźć maksymalną część energii układu, która podczas zderzenia przechodzi w energię sprężystej deformacji. Nie ma tarcia między kamieniami.

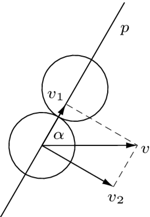
 poruszającego się kamienia na składowe:
poruszającego się kamienia na składowe: 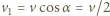 wzdłuż prostej
wzdłuż prostej 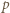 przechodzącej przez środki obu kamieni podczas zderzenia i prostopadłą do niej
przechodzącej przez środki obu kamieni podczas zderzenia i prostopadłą do niej 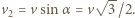 Gdy deformacja jest maksymalna, prędkości kamieni w kierunku
Gdy deformacja jest maksymalna, prędkości kamieni w kierunku 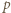 wyrównują się. Oznaczając ich wartość przez
wyrównują się. Oznaczając ich wartość przez 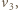 mamy z zasady zachowania pędu
mamy z zasady zachowania pędu 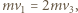 gdzie
gdzie 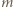 jest masą kamienia, stąd
jest masą kamienia, stąd 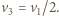 Zasada zachowania energii ma postać:
Zasada zachowania energii ma postać: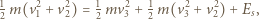
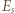 jest maksymalną energią sprężystej deformacji, a jej wartość
jest maksymalną energią sprężystej deformacji, a jej wartość 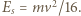 Całkowita energia układu
Całkowita energia układu 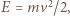 stąd
stąd