Klub 44F - zadania III 2017»Zadanie 635
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania III 2017
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
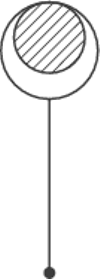
Do dolnego końca pręta o długości 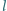 przyczepiono małą kulkę o masie
przyczepiono małą kulkę o masie 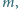 a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu
a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu 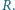 Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy
Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy 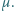 Dla jakich wartości kąta
Dla jakich wartości kąta 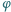 odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?
odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?

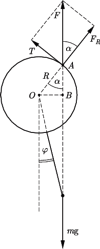
 zaczepiona w środku kulki oraz siły reakcji
zaczepiona w środku kulki oraz siły reakcji 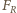 i tarcia
i tarcia 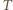 w punkcie
w punkcie 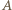 styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt
styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt 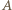 leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień
leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień 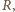 równowaga jest niemożliwa. Gdy kąt
równowaga jest niemożliwa. Gdy kąt 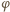 odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość
odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość 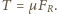 Ponieważ w stanie równowagi wypadkowa
Ponieważ w stanie równowagi wypadkowa 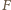 sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek
sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek 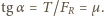 Odcinek
Odcinek 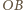 na rysunku możemy wyrazić przez kąty
na rysunku możemy wyrazić przez kąty 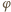 i
i 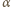 wzorem
wzorem 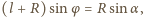 stąd
stąd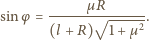
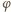 nie zależy od masy kulki. Dla
nie zależy od masy kulki. Dla 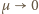 stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy
stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy 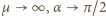 i
i 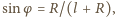 wtedy maksymalne odchylenie kulki w prawo dąży do
wtedy maksymalne odchylenie kulki w prawo dąży do  Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi.
Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi.