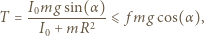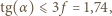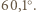Rozważmy staczanie walca (belki) po równi (pochylni), gdy nie występuje poślizg. W każdej chwili tworząca powierzchni walca stykająca się z równią jest (chwilową) osią obrotu. Obrót walca wokół tej osi opisuje równanie:
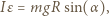
gdzie 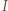 oznacza moment bezwładności walca względem jednej z krawędzi bocznych walca (chwilowej osi obrotu),
oznacza moment bezwładności walca względem jednej z krawędzi bocznych walca (chwilowej osi obrotu), 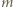 jest masą walca,
jest masą walca,  jego przyspieszeniem kątowym, zaś
jego przyspieszeniem kątowym, zaś 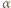 kątem nachylenia równi. Zgodnie z twierdzeniem Steinera, dla walca o promieniu
kątem nachylenia równi. Zgodnie z twierdzeniem Steinera, dla walca o promieniu 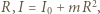 przy czym
przy czym 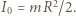 Gdy nie występuje poślizg, przyspieszenie
Gdy nie występuje poślizg, przyspieszenie  ruchu postępowego wzdłuż równi spełnia warunek:
ruchu postępowego wzdłuż równi spełnia warunek:
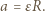
Z drugiej strony, zgodnie z drugą zasadą dynamiki:
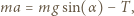
gdzie 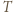 oznacza siłę tarcia statycznego zapewniającą brak poślizgu, a
oznacza siłę tarcia statycznego zapewniającą brak poślizgu, a 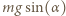 jest składową siły ciężkości wzdłuż równi. Możemy teraz wyznaczyć wartość siły tarcia statycznego:
jest składową siły ciężkości wzdłuż równi. Możemy teraz wyznaczyć wartość siły tarcia statycznego:
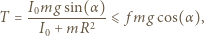
gdzie prawa strona nierówności określa maksymalną wartość siły tarcia statycznego zapobiegającego poślizgowi. Ostatecznie otrzymujemy, że staczanie walca bez poślizgu odbywa się, gdy:
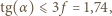
co odpowiada ograniczeniu kąta do 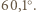
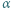 między pochylnią i poziomem, dla której belki staczają się bez poślizgu? Należy przyjąć, że belki mają kształt walców, a współczynnik tarcia statycznego drzewa między powierzchniami z drzewa dębowego wynosi
między pochylnią i poziomem, dla której belki staczają się bez poślizgu? Należy przyjąć, że belki mają kształt walców, a współczynnik tarcia statycznego drzewa między powierzchniami z drzewa dębowego wynosi 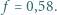

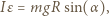
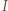 oznacza moment bezwładności walca względem jednej z krawędzi bocznych walca (chwilowej osi obrotu),
oznacza moment bezwładności walca względem jednej z krawędzi bocznych walca (chwilowej osi obrotu), 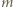 jest masą walca,
jest masą walca,  jego przyspieszeniem kątowym, zaś
jego przyspieszeniem kątowym, zaś 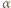 kątem nachylenia równi. Zgodnie z twierdzeniem Steinera, dla walca o promieniu
kątem nachylenia równi. Zgodnie z twierdzeniem Steinera, dla walca o promieniu 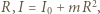 przy czym
przy czym 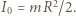 Gdy nie występuje poślizg, przyspieszenie
Gdy nie występuje poślizg, przyspieszenie  ruchu postępowego wzdłuż równi spełnia warunek:
ruchu postępowego wzdłuż równi spełnia warunek: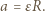
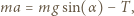
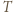 oznacza siłę tarcia statycznego zapewniającą brak poślizgu, a
oznacza siłę tarcia statycznego zapewniającą brak poślizgu, a 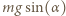 jest składową siły ciężkości wzdłuż równi. Możemy teraz wyznaczyć wartość siły tarcia statycznego:
jest składową siły ciężkości wzdłuż równi. Możemy teraz wyznaczyć wartość siły tarcia statycznego: