Punkty libracji trzech ciał i twierdzenie KAM
W artykule Stabilność układu słonecznego zamieszczonym w Delcie 9/2016 zaanonsowałem zastosowanie teorii Kołmogorowa-Arnolda-Mosera (KAM) do problemu stabilności w zagadnieniu  ciał.
ciał.
Na Międzynarodowym Kongresie Matematyków w Amsterdamie w 1954 roku Andriej Kołmogorow przedstawił swój pomysł na dowód zbieżności tzw. szeregów Poincarégo, które opisują ruch 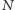 ciał i które stanowią uogólnienie szeregów Fouriera, czyli sum sinusów i kosinusów o częstościach będących wielokrotnościami pewnej częstości podstawowej. Ścisłe dowody zbieżności szeregów Poincarégo zostały podane na początku lat 60. niezależnie przez Władimira Arnolda (ucznia Kołmogorowa) i Jurgena Mosera - twierdzenie KAM.
ciał i które stanowią uogólnienie szeregów Fouriera, czyli sum sinusów i kosinusów o częstościach będących wielokrotnościami pewnej częstości podstawowej. Ścisłe dowody zbieżności szeregów Poincarégo zostały podane na początku lat 60. niezależnie przez Władimira Arnolda (ucznia Kołmogorowa) i Jurgena Mosera - twierdzenie KAM.
We właściwym sformułowaniu twierdzenia KAM mamy do czynienia z układem hamiltonowskim, czyli opisanym za pomocą funkcji Hamiltona, wyrażającej zależność całkowitej energii układu od pędów 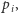 i położeń
i położeń 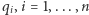 cząstek. Równania opisujące ewolucję takiego układu są równaniami różniczkowymi pierwszego rzędu na pędy oraz położenia i są równoważne układowi równań Newtona, które są równaniami drugiego rzędu na położenia. Funkcja Hamiltona ma następującą postać:
cząstek. Równania opisujące ewolucję takiego układu są równaniami różniczkowymi pierwszego rzędu na pędy oraz położenia i są równoważne układowi równań Newtona, które są równaniami drugiego rzędu na położenia. Funkcja Hamiltona ma następującą postać:

gdzie 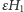 jest małym zaburzeniem, a
jest małym zaburzeniem, a  jest funkcją Hamiltona układu całkowalnego, czyli takiego, który - mówiąc najprościej - umiemy rozwiązać.
jest funkcją Hamiltona układu całkowalnego, czyli takiego, który - mówiąc najprościej - umiemy rozwiązać.
Ściślej, własność całkowalności oznacza, że istnieją tzw. zmienne kąt-działanie 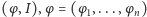 (gdzie
(gdzie 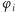 są kątami),
są kątami), 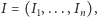 w których odpowiedni układ różniczkowy przyjmuje szczególnie prostą postać:
w których odpowiedni układ różniczkowy przyjmuje szczególnie prostą postać:

Zatem ruch niezaburzony odbywa się na torusach 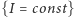 parametryzowanych przez kąty
parametryzowanych przez kąty 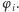 Mamy
Mamy 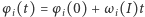 (z dokładnością do
(z dokładnością do  ). Jeśli układ częstości
). Jeśli układ częstości  jest rezonansowy, tj.
jest rezonansowy, tj. 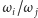 są liczbami wymiernymi, to ruch na torusie jest okresowy (układ po skończonym czasie wraca do punktu początkowego i ruch dalej odbywa się po tej samej trajektorii). W skrajnie przeciwnym przypadku każda trajektoria na torusie jest gęsta (tworzy obmotkę, przebiegając dowolnie blisko każdego punktu); mówimy wtedy, że ruch jest prawie okresowy. Jeśli częstości
są liczbami wymiernymi, to ruch na torusie jest okresowy (układ po skończonym czasie wraca do punktu początkowego i ruch dalej odbywa się po tej samej trajektorii). W skrajnie przeciwnym przypadku każda trajektoria na torusie jest gęsta (tworzy obmotkę, przebiegając dowolnie blisko każdego punktu); mówimy wtedy, że ruch jest prawie okresowy. Jeśli częstości 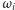 zmieniają się w sposób regularny w zależności od zmian działań
zmieniają się w sposób regularny w zależności od zmian działań 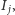 to na większości torusów ruch jest prawie okresowy.
to na większości torusów ruch jest prawie okresowy.
Teza twierdzenia KAM mówi, że jeżeli spełniony jest pewien warunek regularności częstości (nieznikanie pewnych wyznaczników), to przy przejściu od układu niezaburzonego, opisanego przez 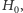 do układu zaburzonego, opisywanego przez
do układu zaburzonego, opisywanego przez 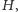 większość torusów niezmienniczych nie znika, tylko lekko się zaburza, i ruch na nich jest prawie okresowy. To, niestety, jeszcze nie gwarantuje stabilności, bo zawsze można tak dobrać dane początkowe
większość torusów niezmienniczych nie znika, tylko lekko się zaburza, i ruch na nich jest prawie okresowy. To, niestety, jeszcze nie gwarantuje stabilności, bo zawsze można tak dobrać dane początkowe 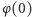 i
i 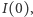 żeby ruch nie leżał na torusie niezmienniczym. Taka sytuacja ma miejsce dla liczby stopni swobody
żeby ruch nie leżał na torusie niezmienniczym. Taka sytuacja ma miejsce dla liczby stopni swobody 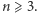
Rys. 1
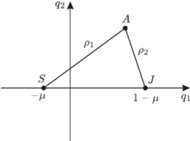
Istnieje jednak spektakularny przykład dla 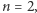 gdzie teoria KAM daje tzw. stabilność w sensie Lapunowa. Jest to tzw. ograniczone zagadnienie 3 ciał. Możemy przyjąć, że te ciała to Słońce
gdzie teoria KAM daje tzw. stabilność w sensie Lapunowa. Jest to tzw. ograniczone zagadnienie 3 ciał. Możemy przyjąć, że te ciała to Słońce 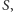 Jowisz
Jowisz 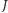 i Asteroida
i Asteroida 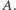 Przy tym zakłada się, że
Przy tym zakłada się, że 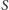 i
i 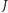 poruszają się w stałej płaszczyźnie po orbitach kołowych ze stałą częstością, natomiast
poruszają się w stałej płaszczyźnie po orbitach kołowych ze stałą częstością, natomiast 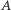 porusza się w tej samej płaszczyźnie pod wpływem pola grawitacyjnego wytwarzanego przez
porusza się w tej samej płaszczyźnie pod wpływem pola grawitacyjnego wytwarzanego przez 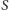 i
i 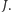 Masa
Masa 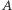 jest zaniedbywalnie mała. Po przejściu do układu położeń
jest zaniedbywalnie mała. Po przejściu do układu położeń 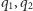 i odpowiednich pędów
i odpowiednich pędów 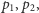 takich że
takich że 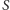 i
i 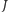 spoczywają (oraz wyborze odpowiednich jednostek fizycznych), funkcja Hamiltona opisująca ruch
spoczywają (oraz wyborze odpowiednich jednostek fizycznych), funkcja Hamiltona opisująca ruch 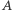 wygląda następująco:
wygląda następująco:

gdzie 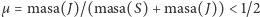 a
a 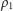 i
i 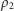 są odległościami
są odległościami 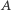 od
od 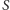 i
i  odpowiednio (Rys. 1).
odpowiednio (Rys. 1).
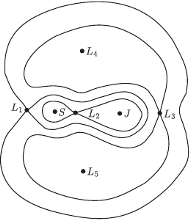
Rys. 2
Punkty równowagi odpowiedniego układu hamiltonowskiego, nazywane punktami libracji, są punktami krytycznymi funkcji 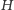 (lokalne minima, maksima lub punkty siodłowe). Są one jednoznacznie wyznaczone przez punkty krytyczne funkcji
(lokalne minima, maksima lub punkty siodłowe). Są one jednoznacznie wyznaczone przez punkty krytyczne funkcji 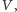 której poziomice (krzywe, na których wartość
której poziomice (krzywe, na których wartość 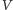 jest stała) są naszkicowane na rysunku 2 Mamy tzw. współliniowe punkty libracji
jest stała) są naszkicowane na rysunku 2 Mamy tzw. współliniowe punkty libracji 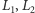 i
i 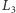 na osi
na osi 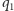 i tzw. trójkątne punkty libracji (nazywane też punktami libracji Lagrange'a)
i tzw. trójkątne punkty libracji (nazywane też punktami libracji Lagrange'a) 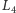 i
i 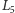 w wierzchołkach trójkątów równobocznych o boku
w wierzchołkach trójkątów równobocznych o boku 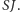 Punkty
Punkty 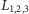 są niestabilne dla układu Hamiltona już w przybliżeniu liniowym. Oznacza to, że umieszczona w tym punkcie Asteroida będzie pozostawać w spoczynku, ale dowolnie małe wychylenie jej z tego położenia spowoduje, że zacznie oddalać się od tego punktu, tak jak piłka położona na szczycie pagórka wytrącona z położenia równowagi zaczyna staczać się po zboczu.
są niestabilne dla układu Hamiltona już w przybliżeniu liniowym. Oznacza to, że umieszczona w tym punkcie Asteroida będzie pozostawać w spoczynku, ale dowolnie małe wychylenie jej z tego położenia spowoduje, że zacznie oddalać się od tego punktu, tak jak piłka położona na szczycie pagórka wytrącona z położenia równowagi zaczyna staczać się po zboczu.
W punktach 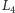 i
i 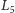 rozwinięcie funkcji
rozwinięcie funkcji 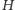 w szereg Taylora i zastosowanie pewnej subtelnej redukcji (pochodzącej of George'a Birkhoffa) daje nową funkcję Hamiltona postaci
w szereg Taylora i zastosowanie pewnej subtelnej redukcji (pochodzącej of George'a Birkhoffa) daje nową funkcję Hamiltona postaci 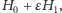 do której daje się zastosować twierdzenie KAM. Ściślej, w przybliżeniu kwadratowym mamy
do której daje się zastosować twierdzenie KAM. Ściślej, w przybliżeniu kwadratowym mamy

gdzie 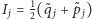 a
a 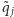 i
i 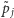 są odpowiednimi funkcjami liniowymi (uogólnione położenia i pędy) zerującymi się w
są odpowiednimi funkcjami liniowymi (uogólnione położenia i pędy) zerującymi się w  (odpowiednio
(odpowiednio 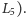 Gdyby zamiast minusa w powyższym wzorze był plus, to funkcja
Gdyby zamiast minusa w powyższym wzorze był plus, to funkcja 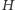 (która nie zmienia się w trakcie ruchu) miałaby lokalne minimum w
(która nie zmienia się w trakcie ruchu) miałaby lokalne minimum w 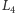 i własność stabilności byłaby automatyczna. Moglibyśmy też przyjąć
i własność stabilności byłaby automatyczna. Moglibyśmy też przyjąć 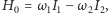 a wyrazy wyższego rzędu potraktować jako zaburzenie
a wyrazy wyższego rzędu potraktować jako zaburzenie 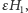 ale wtedy nie byłoby spełnione założenie twierdzenia KAM o regularnej zależności częstości od działań.
ale wtedy nie byłoby spełnione założenie twierdzenia KAM o regularnej zależności częstości od działań.
Dlatego potrzebna jest dalsza redukcja, w wyniku której dostaniemy 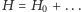 z
z 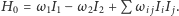 Przy tym należy odrzucić wartości parametru
Przy tym należy odrzucić wartości parametru 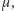 odpowiadające rezonansom niskich rzędów, tj.
odpowiadające rezonansom niskich rzędów, tj. 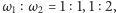
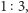 oraz dodatkowej wartości
oraz dodatkowej wartości 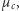 związanej z warunkiem zdegenerowania zależności
związanej z warunkiem zdegenerowania zależności 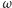 od
od 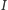 (wyliczonej przez André Deprit i Andrée Deprit-Bartholomé).
(wyliczonej przez André Deprit i Andrée Deprit-Bartholomé).
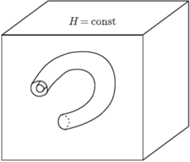
Rys. 3
Teraz stabilność położeń równowagi 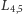 wynika z następujących rozważań. Ponieważ funkcja
wynika z następujących rozważań. Ponieważ funkcja 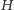 jest całką ruchu (jest ona stała na rozwiązaniach), to jej poziomice
jest całką ruchu (jest ona stała na rozwiązaniach), to jej poziomice 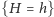 są niezmienniczymi
są niezmienniczymi  -wymiarowymi hiperpowierzchniami w przestrzeni fazowej zmiennych
-wymiarowymi hiperpowierzchniami w przestrzeni fazowej zmiennych 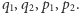 Na każdej takiej poziomicy mamy dużo torusów niezmienniczych i każdy z nich rozcina poziomicę na dwa obszary, wnętrze i zewnętrze. Punkty z wnętrz nie wychodzą z nich w trakcie ewolucji i pozostają blisko punktu równowagi (Rys. 3).
Na każdej takiej poziomicy mamy dużo torusów niezmienniczych i każdy z nich rozcina poziomicę na dwa obszary, wnętrze i zewnętrze. Punkty z wnętrz nie wychodzą z nich w trakcie ewolucji i pozostają blisko punktu równowagi (Rys. 3).
Na koniec warto dodać, że są obserwowane gromady asteroid w trójkątnych punktach libracji związanych zarówno z parą Słońce-Jowisz, jak i z innymi parami. W przypadkach silnych rezonansów (jak te wyróżnione powyżej) takich asteroid brak.