Stabilność Układu Słonecznego

Od czasów Newtona znane są prawa rządzące ruchem ciał podlegających siłom przyciągania grawitacyjnego. Dla izolowanego układu 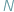$N$ ciał dostajemy układ 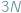$3N$ równań różniczkowych drugiego rzędu (po trzy na współrzędne środka masy każdego ciała), który ma jednoznaczne rozwiązanie przy zadanych położeniach i prędkościach początkowych. W istocie, można ograniczyć się do układu współrzędnych związanego ze środkiem masy całego układu i liczba równań redukuje się do 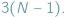$|3(N − 1):$ Tak precyzyjnie sformułowane zagadnienie nosi nazwę problemu 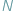$|N$ ciał.

Niestety, ścisłe rozwiązania tych równań zostały znalezione tylko w szczególnych przypadkach. Najważniejszym z nich jest zagadnienie Keplera, czyli problem dwóch ciał. Z pierwszego prawa Keplera (zasada zachowania momentu pędu) wynika, że oba ciała poruszają się w nieruchomej płaszczyźnie. Całkowanie odpowiednich równań w biegunowym układzie współrzędnych 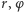$r,φ$ (w tej płaszczyźnie) pokazuje, że trajektoria każdego ciała jest opisana równaniem postaci

A r = 1+-εcosφ-,

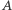gdzie $A$ jest amplitudą, a 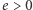$e | > 0$ jest mimośrodem orbity. Powyższe równanie opisuje krzywą stożkową. Dla 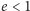$| e < 1$ jest to elipsa z ogniskiem w środku masy, a odpowiednie rozwiązania układu Newtona są okresowe.

Ciekawe rozwiązanie zagadnienia trzech ciał zostało znalezione przez Lagrange'a. Tutaj trzy ciała leżą w wierzchołkach trójkąta równobocznego obracającego się wokół środka masy w ustalonej płaszczyźnie.

Na Marginesie

Wszystkie planety obiegają Słońce po orbitach bardzo zbliżonych do elips będących rozwiązaniem odpowiedniego układu dwóch ciał dla $ε@ 1.$ Podobnie niektóre komety. Obserwujemy jednak również komety mające orbity paraboliczne bądź hiperboliczne (np. C/1980 E1 (Bowell); $|ε 1,057$ ).

Równanie elipsy uzyskuje się z praktycznego sposobu na jej rysowanie: wbijamy w podłoże dwie pinezki połączone sznurkiem o długości $2a$ i rysujemy wszystkie punkty (nazwijmy je położeniami planety), które zakreśli ołówek napinający sznurek. Jedną z pinezek nazwijmy Słońcem i oznaczmy $|S,$ a jedno z położeń planety $P.$ W układzie współrzędnych biegunowych (o początku $S$ i osi łączącej pinezki) planetę $P$ opisują $|r$ i $φ.$

Odległość między pinezkami musi być mniejsza od długości sznurka, oznaczmy ją $|2a ε,$ gdzie $ε @1$ nazywany jest mimośrodem. Z twierdzenia kosinusów mamy

r2 4a2ε 2 4raεcosφ 2a r 2.

Otwierając nawias, redukując $r2$ i dzieląc obustronnie przez $4a$ otrzymujemy $| 2 aε rεcosφ a r,$ czyli $| 2 r 1 εcosφ a 1 ε ,$ a więc równanie orbity planety podane w głównym tekście.

Naturalnym układem grawitacyjnym jest nasz Układ Słoneczny (z dyskusyjną, ale znacznie większą od 2 liczbą 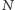$N$ ). Mimo iż nikt nie porywał się na rozwiązywanie skomplikowanego układu równań z nim związanego, to jednak problemu stabilności naszego sytemu nie można zignorować. Jest to pytanie, czy układ planetarny będzie zachowywał obecny kształt w odległej przyszłości, czy któraś z planet może go opuścić lub jakaś kolizja może spowodować jego dramatyczną zmianę.

Ta kwestia stała się swego rodzaju obsesją XIX wieku i była na tyle istotna, że w 1885 roku król szwedzki, Oskar II, ufundował nagrodę za postęp w tej sprawie. Nagrodę dostał Henri Poincaré, ale trzeba uczciwie powiedzieć, że ani on, ani nikt inny do tej pory nie podał ścisłego matematycznego dowodu stabilności układu 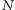$N$ ciał. W tym miejscu należy wymienić także nazwiska Karla Weierstrassa, Sophie Kowalewskiej i Petera Dirichleta, którzy aktywnie pracowali nad tym problemem.

Metoda stosowana przez XIX-wiecznych matematyków startowała od szeregów typu Fouriera. W pierwszym przybliżeniu zakładano, że Słońce jest nieruchome, a każda z planet porusza się ruchem okresowym (z okresem 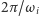$|2π/ω$ ) po orbicie eliptycznej. Zatem położenie 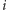$i$ -tej planety zadane jest szeregiem Fouriera

∞ Q Amcos(m m

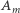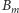z wektorami $Am$ i $Bm |$ zależnymi od danych początkowych. Następnie sukcesywnie uwzględniano się siły wzajemnych oddziaływań planet i ruch samego Słońca. Wprowadzenie tych zaburzeń prowadzi do tzw. szeregów Poincarégo. Niestety, nie można w rozsądny sposób zapewnić zbieżności tych szeregów.

Pewien postęp w tej sprawie uzyskano dopiero na przełomie lat pięćdziesiątych i sześćdziesiątych XX wieku - jest on znany jako twierdzenie KAM od nazwisk jego twórców: Andrieja Kołmogorowa, Władimira Arnolda i Jürgena Mosera. Ale o tym napiszę w następnym numerze Delty.