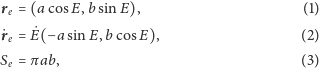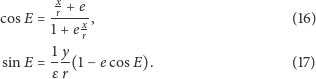Jak one obiegają?
Johannes Kepler wyprowadził swoje pierwsze dwa prawa, analizując obserwacje
Marsa wykonane przez Tychona Brahego. Po stuleciach obserwacji okresy
orbitalne (lata) Ziemi i Marsa,
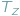 i
i
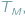 były wtedy znane bardzo
dokładnie...
były wtedy znane bardzo
dokładnie...
Kepler przytomnie zauważył, że po upływie każdego swojego roku Mars
znajduje się w tym samym punkcie przestrzeni, ale obserwowany jest z innego
punktu ziemskiej orbity, jako że w tym czasie Ziemia obiega całą swoją orbitę
i jeszcze dodatkowy łuk, którego długość łatwo obliczyć, znając różnicę
obu okresów. Znając ów łuk, Kepler mógł wyznaczyć długość boku
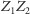 trójkąta
trójkąta
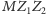 o wierzchołkach w początkowym
położeniu Marsa
o wierzchołkach w początkowym
położeniu Marsa
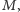 początkowym położeniu Ziemi
początkowym położeniu Ziemi
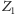 oraz
położeniu Ziemi po upływie marsjańskiego roku
oraz
położeniu Ziemi po upływie marsjańskiego roku
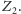 Kąty przy boku
Kąty przy boku
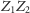 były znane dzięki obserwacjom Brahego, co pozwoliło Keplerowi
wyznaczyć przestrzenne położenie Marsa. Powtarzając procedurę dla
innych punktów orbity Marsa, Kepler określił kształt całej tej orbity,
łącznie z informacją o czasie przejścia przez każdy punkt. Tu był tylko
o jeden krok od empirycznego stwierdzenia, że orbita jest elipsą, a Słońce
znajduje się w jej ognisku (pierwsze prawo Keplera), i że linia łącząca
Słońce z planetą, tzw. promień wodzący, zakreśla równą część pola
orbity w równym czasie (drugie prawo Keplera). Dopiero potem Newton
wykazał teoretycznie, że z jego praw dynamiki i prawa grawitacji wynikają
prawa Keplera.
były znane dzięki obserwacjom Brahego, co pozwoliło Keplerowi
wyznaczyć przestrzenne położenie Marsa. Powtarzając procedurę dla
innych punktów orbity Marsa, Kepler określił kształt całej tej orbity,
łącznie z informacją o czasie przejścia przez każdy punkt. Tu był tylko
o jeden krok od empirycznego stwierdzenia, że orbita jest elipsą, a Słońce
znajduje się w jej ognisku (pierwsze prawo Keplera), i że linia łącząca
Słońce z planetą, tzw. promień wodzący, zakreśla równą część pola
orbity w równym czasie (drugie prawo Keplera). Dopiero potem Newton
wykazał teoretycznie, że z jego praw dynamiki i prawa grawitacji wynikają
prawa Keplera.
Dyskusję zagadnienia ruchu planet w potencjale grawitacyjnym Słońca, czyli tzw. problem Keplera, zazwyczaj przedstawia się dopiero na poziomie studiów uniwersyteckich, mimo że nie wymaga ona używania skomplikowanych pojęć fizycznych ani zaawansowanej matematyki. W tym artykule postaramy się rozwiązać elementarnie problem Keplera – pokazując, że empiryczne prawa Keplera, opisujące ruch planet, są zgodne z prawami dynamiki Newtona.
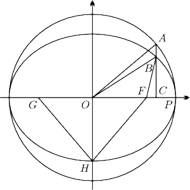
Wyjdziemy od zwykłego jednostajnego ruchu po okręgu o promieniu
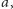 umieszczając środek
umieszczając środek
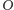 tego okręgu w początku układu
współrzędnych, tak jak na rysunku obok. Wektor wodzący
tego okręgu w początku układu
współrzędnych, tak jak na rysunku obok. Wektor wodzący
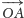 punktu
punktu
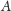 na okręgu można wówczas opisać jako
na okręgu można wówczas opisać jako

gdzie
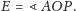 Prędkość ruchu jest styczna do okręgu, a więc
prostopadła do promienia, zatem
Prędkość ruchu jest styczna do okręgu, a więc
prostopadła do promienia, zatem

gdzie przez
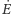 oznaczamy tempo zmiany kąta
oznaczamy tempo zmiany kąta
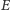 (prędkość
kątową). Oczywiście, pole koła ograniczonego przez rozważany okrąg
jest równe
(prędkość
kątową). Oczywiście, pole koła ograniczonego przez rozważany okrąg
jest równe
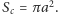
Jeżeli na płaszczyznę zawierającą opisany wyżej okrąg będziemy patrzeć
nie „z góry”, ale „z ukosa”, zobaczymy nie okrąg, ale elipsę o wielkiej półosi
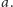 Załóżmy, że patrzymy z takiego kierunku, że wskutek rzutowania
współrzędne
Załóżmy, że patrzymy z takiego kierunku, że wskutek rzutowania
współrzędne
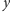 ulegają skróceniu o czynnik
ulegają skróceniu o czynnik
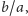 gdzie
gdzie
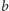 to długość
to długość
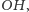 a współrzędne
a współrzędne
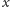 nie zmieniają się.
Oczywiście, zmniejszeniu o taki sam czynnik ulegną także składowa
nie zmieniają się.
Oczywiście, zmniejszeniu o taki sam czynnik ulegną także składowa
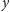 prędkości oraz pole powierzchni elipsy względem odpowiednich
wielkości dla okręgu:
prędkości oraz pole powierzchni elipsy względem odpowiednich
wielkości dla okręgu:
gdzie
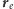 to wektor
to wektor
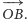 Kąt
Kąt
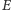 nazywamy teraz
anomalią mimośrodową. Ogniskami elipsy będą takie punkty
nazywamy teraz
anomalią mimośrodową. Ogniskami elipsy będą takie punkty
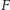 i
i
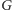 na osi
na osi
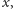 że suma ich odległości od dowolnego punktu elipsy
będzie stała i równa
że suma ich odległości od dowolnego punktu elipsy
będzie stała i równa
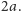 Jeśli długości odcinków
Jeśli długości odcinków
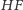 i
i
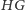 są równe
są równe
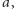 zaś długości odcinków
zaś długości odcinków
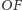 i
i
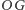 są równe
są równe
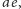 gdzie
gdzie
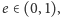 to z twierdzenia
Pitagorasa dla trójkąta
to z twierdzenia
Pitagorasa dla trójkąta
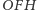 mamy
mamy
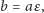 | (4) |
gdzie
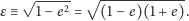 | (5) |
Zauważmy, że rzutowanie zachowuje równoległość wektorów, ale
prostopadłości już nie. Wynika stąd w szczególności, że rzutowana
prędkość w
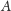 pozostaje styczna do toru w
pozostaje styczna do toru w
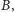 ale nie jest już
prostopadła do
ale nie jest już
prostopadła do
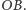 Jeśli przeniesiemy układ współrzędnych do
Jeśli przeniesiemy układ współrzędnych do
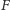 (lub
(lub
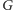 ), promień wodzący
), promień wodzący
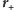 (
(
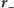 ) otrzymamy,
odejmując od
) otrzymamy,
odejmując od
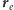 wektor
wektor
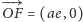 (lub
(lub
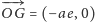 ),
a prędkość zostanie ta sama:
),
a prędkość zostanie ta sama:
Powyższe wzory opisują tor zgodny z pierwszym prawem Keplera, tj. elipsę.
Obliczając długości
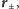 łatwo przekonać się, że odległości
łatwo przekonać się, że odległości
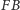 i
i
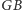 punktu
punktu
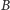 od ognisk
od ognisk
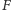 i
i
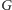 wynoszą
wynoszą
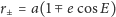 | (8) |
i ich suma rzeczywiście jest stała i równa
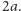 Ponadto, ze wzoru (8)
wynika, że minimalna odległość od ogniska
Ponadto, ze wzoru (8)
wynika, że minimalna odległość od ogniska
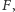 wynosząca
wynosząca
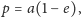 jest osiągana w punkcie
jest osiągana w punkcie
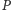 dla
dla
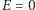 ;
punkt ten nazywamy perihelium. Kosinus kąta między prędkością
;
punkt ten nazywamy perihelium. Kosinus kąta między prędkością
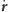 a promieniem wodzącym
a promieniem wodzącym
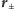 jest proporcjonalny do ich iloczynu
skalarnego i odwrotnie proporcjonalny do długości każdego z tych
wektorów. Skoro zaś
jest proporcjonalny do ich iloczynu
skalarnego i odwrotnie proporcjonalny do długości każdego z tych
wektorów. Skoro zaś
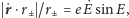 kąty te dla ognisk
kąty te dla ognisk
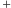 i
i
 są położone symetrycznie względem
są położone symetrycznie względem
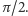 Wynika stąd
w szczególności, że promień światła wysłany z jednego ogniska i odbity
zgodnie z prawami optyki geometrycznej od elipsy trafi w drugie ognisko.
W dalszych rozważaniach nie będziemy już się więcej zajmować ogniskiem
Wynika stąd
w szczególności, że promień światła wysłany z jednego ogniska i odbity
zgodnie z prawami optyki geometrycznej od elipsy trafi w drugie ognisko.
W dalszych rozważaniach nie będziemy już się więcej zajmować ogniskiem
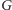 i opuścimy indeks
i opuścimy indeks
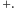
W sposób czysto empiryczny, porównując wartości okresów
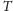 i półosi
i półosi
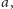 Kepler odkrył jako trzecie prawo, że
Kepler odkrył jako trzecie prawo, że
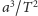 jest stałe. Postać
tej stałej znalazł dopiero Newton, pokazując, że
jest stałe. Postać
tej stałej znalazł dopiero Newton, pokazując, że
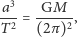 | (9) |
gdzie
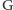 i
i
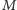 to stała grawitacji i masa Słońca. Dopiero
z ostatniego wzoru tego artykułu przekonamy się, że właśnie taki wybór stałej
jest poprawny. Jednak dla konkretnej planety
to stała grawitacji i masa Słońca. Dopiero
z ostatniego wzoru tego artykułu przekonamy się, że właśnie taki wybór stałej
jest poprawny. Jednak dla konkretnej planety
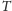 i
i
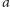 pozostają stałe
i ich związek nie ma znaczenia w rozważaniach ruchu.
pozostają stałe
i ich związek nie ma znaczenia w rozważaniach ruchu.
Dotąd nie zajmowaliśmy się czasem
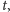 w którym jest osiągany
punkt
w którym jest osiągany
punkt
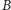 na elipsie, o ile znamy moment
na elipsie, o ile znamy moment
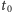 przejścia przez
perihelium
przejścia przez
perihelium
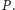 To zagadnienie Kepler rozwiązał w oparciu o prawo
stałych pól. Cała powierzchnia elipsy
To zagadnienie Kepler rozwiązał w oparciu o prawo
stałych pól. Cała powierzchnia elipsy
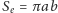 jest zakreślana
w czasie jednego okresu
jest zakreślana
w czasie jednego okresu
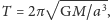 stąd prędkość polowa to
stąd prędkość polowa to
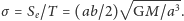 Na podstawie prawa pól Kepler przyjął, że
pole
Na podstawie prawa pól Kepler przyjął, że
pole
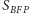 wycinka elipsy zawartego w
wycinka elipsy zawartego w
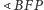 jest proporcjonalne
do przedziału czasu:
jest proporcjonalne
do przedziału czasu:
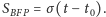 Następnie zauważył, że
Następnie zauważył, że
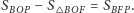 To równanie Keplera było kluczem do rozwiązania
problemu. Wycinek elipsy
To równanie Keplera było kluczem do rozwiązania
problemu. Wycinek elipsy
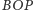 jest rzutem wycinka koła
jest rzutem wycinka koła
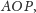 stąd
jego pole jest równe
stąd
jego pole jest równe
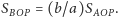 Z wyznaczeniem pola trójkąta
Z wyznaczeniem pola trójkąta
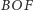 o znanych współrzędnych wierzchołków uczony poradził sobie
bez trudu i ostatecznie przedstawił (w 1619 roku) równanie w postaci
o znanych współrzędnych wierzchołków uczony poradził sobie
bez trudu i ostatecznie przedstawił (w 1619 roku) równanie w postaci
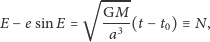 | (10) |
gdzie kąt
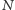 jest zwany anomalią średnią, a stała proporcjonalności
została uwspółcześniona. Czytelnik Wnikliwy może sprawdzić, jaki to stały
czynnik uczony uprościł w polach, podając wzór w postaci (10). Ponieważ po
okresie obiegu
jest zwany anomalią średnią, a stała proporcjonalności
została uwspółcześniona. Czytelnik Wnikliwy może sprawdzić, jaki to stały
czynnik uczony uprościł w polach, podając wzór w postaci (10). Ponieważ po
okresie obiegu
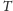 lewa strona równania (10) rośnie o
lewa strona równania (10) rośnie o
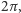 zatem
to samo robi prawa strona:
zatem
to samo robi prawa strona:
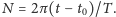 Równanie Keplera nie ma
rozwiązania analitycznego, ale dla danego
Równanie Keplera nie ma
rozwiązania analitycznego, ale dla danego
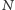 wartość rozwiązania
wartość rozwiązania
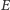 można szybko obliczyć metodą Newtona. Przyjmując pierwsze
przybliżenie rozwiązania, np. jako
można szybko obliczyć metodą Newtona. Przyjmując pierwsze
przybliżenie rozwiązania, np. jako
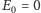 lub
lub
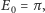 następne
otrzymuje się ze wzoru
następne
otrzymuje się ze wzoru
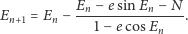 | (11) |
Dla rosnącego
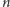 iteracje są szybko zbieżne do prawdziwego rozwiązania
iteracje są szybko zbieżne do prawdziwego rozwiązania
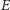 spełniającego zależność (10).
spełniającego zależność (10).
Posłużymy się równaniem Keplera do obliczenia chwilowej prędkości
kątowej
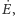 a stąd prędkości liniowej
a stąd prędkości liniowej
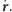 W tym celu
zastanówmy się nad prędkością zmian każdej ze stron wzoru (10).
Czynnik z pierwiastkiem jest stały, mamy więc do czynienia z „ruchem
jednostajnym” z prędkością
W tym celu
zastanówmy się nad prędkością zmian każdej ze stron wzoru (10).
Czynnik z pierwiastkiem jest stały, mamy więc do czynienia z „ruchem
jednostajnym” z prędkością
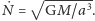 Po lewej stronie wzoru (10)
prędkość zmian
Po lewej stronie wzoru (10)
prędkość zmian
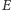 jest po prostu
jest po prostu
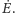 Pozostaje zatem
określić prędkość zmian wyrazu
Pozostaje zatem
określić prędkość zmian wyrazu
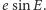 Wybierzmy sobie punkt
o współrzędnej
Wybierzmy sobie punkt
o współrzędnej
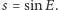 W czasie ruchu stosunek tej współrzędnej do
W czasie ruchu stosunek tej współrzędnej do
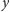 na elipsie pozostaje stały:
na elipsie pozostaje stały:
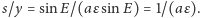 Zatem
stosunek tempa ich zmian w czasie
Zatem
stosunek tempa ich zmian w czasie
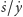 musi być identyczny, więc
ze wzoru (7),
musi być identyczny, więc
ze wzoru (7),
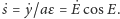 Mnożenie przez
Mnożenie przez
 odpowiada
jedynie zmianie jednostek, zatem prędkość zmian
odpowiada
jedynie zmianie jednostek, zatem prędkość zmian
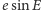 wynosi
wynosi
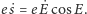 Podsumowując rozważania o prędkościach zmian obu
stron równania Keplera, otrzymujemy:
Podsumowując rozważania o prędkościach zmian obu
stron równania Keplera, otrzymujemy:

Zatem
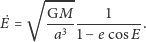 | (12) |
Po drodze otrzymaliśmy użyteczny wzór na
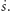 Postępując
podobnie dla
Postępując
podobnie dla
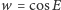 i zmian położenia
i zmian położenia
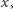 otrzymujemy
odpowiednio:
otrzymujemy
odpowiednio:
Czytelnik Wnikliwy zakrzyknie zaraz ze zgrozą, że przed chwilą po prostu wykonaliśmy różniczkowanie. Prawda to, ale korzystaliśmy tu nie tyle z rachunku różniczkowego, co z intymnego związku pochodnej z prędkością. Podstawiając wzór (12) do (7),
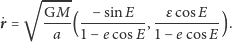 | (15) |
Moment pędu planety o masie
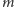 to
to
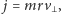 gdzie
gdzie
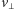 jest składową prędkości prostopadłą do
jest składową prędkości prostopadłą do
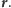 W bardzo
krótkim przedziale czasu
W bardzo
krótkim przedziale czasu
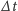 ruch planety może być traktowany
jako prostoliniowy z przesunięciem
ruch planety może być traktowany
jako prostoliniowy z przesunięciem
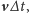 tak że zakreślony
obszar jest wydłużonym trójkątem o boku
tak że zakreślony
obszar jest wydłużonym trójkątem o boku
 i wysokości
i wysokości
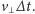 Jego pole to
Jego pole to
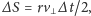 zatem prędkość polowa
zatem prędkość polowa
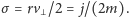 A zatem keplerowskie prawo stałych pól odpowiada
newtonowskiemu prawu zachowania momentu pędu, gdy działająca siła nie ma
składowej prostopadłej do promienia.
A zatem keplerowskie prawo stałych pól odpowiada
newtonowskiemu prawu zachowania momentu pędu, gdy działająca siła nie ma
składowej prostopadłej do promienia.
Dla
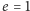 wzór (6) załamuje się, bo
wzór (6) załamuje się, bo
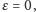 zatem zawsze
zatem zawsze
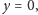 chyba
że
chyba
że
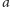 staje się wielkie:
staje się wielkie:
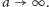 Ponadto we wzorze (12) dla
Ponadto we wzorze (12) dla
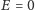 prędkość kątowa staje się wielka,
prędkość kątowa staje się wielka,
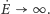 By uniknąć
tych problemów, wyrazimy
By uniknąć
tych problemów, wyrazimy
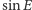 i
i
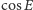 poprzez składowe
jednostkowego wektora kierunkowego
poprzez składowe
jednostkowego wektora kierunkowego
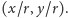 Ze wzorów
(6) i (8) mamy
Ze wzorów
(6) i (8) mamy
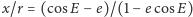 i podobnie
i podobnie
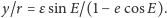 Rozwiązując względem
Rozwiązując względem
 oraz
oraz
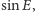 mamy
mamy
Teraz możemy podstawić (16) i (17) do wzoru (15), otrzymując
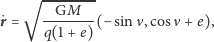 | (18) |
gdzie zamiast
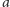 mamy
mamy
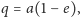 a potęgi
a potęgi
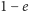 uprościliśmy.
Przy tym nowy kąt
uprościliśmy.
Przy tym nowy kąt
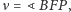 zwany anomalią prawdziwą, wybrano tak,
by
zwany anomalią prawdziwą, wybrano tak,
by
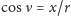 i
i
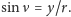 Taki wzór na prędkość to
równanie parametryczne okręgu o środku przesuniętym o
Taki wzór na prędkość to
równanie parametryczne okręgu o środku przesuniętym o
 względem
środka układu. W tym wzorze nie dzieje się nic osobliwego dla
względem
środka układu. W tym wzorze nie dzieje się nic osobliwego dla
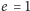 i można oczekiwać, że stosuje się on do ruchu keplerowskiego
po paraboli
i można oczekiwać, że stosuje się on do ruchu keplerowskiego
po paraboli
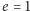 i po hiperboli
i po hiperboli
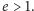 Przy tym dla paraboli
początek układu
Przy tym dla paraboli
początek układu
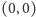 leży na obwodzie, czyli prędkość dąży do
leży na obwodzie, czyli prędkość dąży do
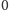 dla
dla
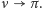 Natomiast dla
Natomiast dla
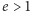 początek leży poza
okręgiem prędkości, zatem prędkość nigdy nie spada do zera, a jej
kierunek musi się zawierać w kącie ograniczonym stycznymi do okręgu
wyprowadzonymi z początku układu. Z zachowania prędkości polowej wynika,
że w perihelium, dla
początek leży poza
okręgiem prędkości, zatem prędkość nigdy nie spada do zera, a jej
kierunek musi się zawierać w kącie ograniczonym stycznymi do okręgu
wyprowadzonymi z początku układu. Z zachowania prędkości polowej wynika,
że w perihelium, dla
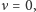 prędkość ma być największa – zatem
tylko dalsza od początku część okręgu pomiędzy stycznymi odpowiada
rzeczywistemu ruchowi po hiperboli.
prędkość ma być największa – zatem
tylko dalsza od początku część okręgu pomiędzy stycznymi odpowiada
rzeczywistemu ruchowi po hiperboli.
Przyspieszenie
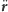 to szybkość zmiany prędkości
to szybkość zmiany prędkości
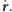 Jedyna
wielkość zmienna we wzorze (18) to
Jedyna
wielkość zmienna we wzorze (18) to
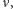 zatem, wykorzystując
równania (14) i (13) dla prędkości zmian tej wielkości, mamy
zatem, wykorzystując
równania (14) i (13) dla prędkości zmian tej wielkości, mamy

Prędkość kątową
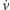 trzeba wyznaczyć z prędkości polowej
trzeba wyznaczyć z prędkości polowej
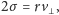 gdzie po prostu
gdzie po prostu
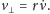 Mamy zatem
Mamy zatem
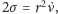 stąd
stąd
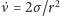 i ostatecznie
i ostatecznie
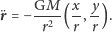 | (19) |
W ten sposób powtórzyliśmy dowód Newtona, że prawa Keplera wymagają
ruchu z przyspieszeniem proporcjonalnym do
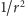 i skierowanym do
obieganego ciała w ognisku elipsy. To, że siła ma być proporcjonalna do
i skierowanym do
obieganego ciała w ognisku elipsy. To, że siła ma być proporcjonalna do
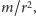 gdzie
gdzie
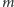 to masa planety, wynika z drugiego prawa
dynamiki, natomiast proporcjonalność do masy
to masa planety, wynika z drugiego prawa
dynamiki, natomiast proporcjonalność do masy
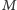 Słońca (drugiego
ciała) wynika z trzeciej zasady dynamiki i założenia symetrii prawa grawitacji
względem obu przyciągających się ciał.
Słońca (drugiego
ciała) wynika z trzeciej zasady dynamiki i założenia symetrii prawa grawitacji
względem obu przyciągających się ciał.
W całych rozważaniach popełniliśmy dwie niedokładności: zaniedbaliśmy ruch Słońca wokół środka masy układu dwóch ciał oraz przyciąganie innych planet. Z prawa ciążenia powszechnego wynika przyciąganie się wszystkich ciał układu słonecznego, a nie tylko Słońca i danej planety. Pomijając to, popełniliśmy błąd, wskutek którego rzeczywiste położenie planety na niebie może oscylować względem obliczonego o wielkość tarczy Księżyca. W rachunkach bardziej ścisłych oblicza się poprawki do przestrzennej orbity keplerowskiej lub dopasowuje się chwilową orbitę keplerowską styczną do prawdziwej, zwaną orbitą oskulacyjną. Oczywiście, jej parametry będą się nieco różnić od wyjściowych i będą również zmieniać się w czasie.