Co to jest?
Elementarne wyprowadzenie równoważności masy i energii
Przedstawione tu wyprowadzenie prawa równoważności, dotychczas nigdzie nie publikowane, ma dwie zalety. Chociaż wykorzystuje się w nim szczególną zasadę względności, nie wymaga to jednak stosowania formalnego aparatu teorii.
Dowód opiera się jedynie na trzech znanych wcześniej prawach:
- (1)
- zasadzie zachowania pędu,
- (2)
- wyrażeniu na pęd promieniowania, czyli - pęd pakietu falowego poruszającego się w danym kierunku,
- (3)
- znanym wyrażeniu dla aberracji światła (wpływu ruchu Ziemi na widziane z Ziemi położenie nieruchomych gwiazd, czyli - na prawie Bradleya).

Rozpatrzmy teraz następujący układ. Niech ciało 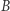 spoczywa swobodnie w przestrzeni względem układu odniesienia
spoczywa swobodnie w przestrzeni względem układu odniesienia 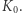 Dwa pakiety falowe
Dwa pakiety falowe 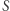 i
i 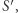 o energii
o energii 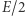 każdy, poruszają się odpowiednio w dodatnim i ujemnym kierunku osi
każdy, poruszają się odpowiednio w dodatnim i ujemnym kierunku osi 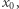 padają na ciało i są przez nie pochłonięte. W wyniku tego procesu energia ciała zwiększa się o
padają na ciało i są przez nie pochłonięte. W wyniku tego procesu energia ciała zwiększa się o 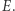 Ciało
Ciało 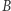 pozostaje przy tym w spoczynku względem układu
pozostaje przy tym w spoczynku względem układu 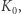 a wynika to z symetrii zagadnienia. Rozważmy teraz ten sam proces z układu odniesienia
a wynika to z symetrii zagadnienia. Rozważmy teraz ten sam proces z układu odniesienia 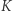 poruszającego się względem układu
poruszającego się względem układu 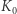 ze stałą prędkością o wartości
ze stałą prędkością o wartości  w ujemnym kierunku osi
w ujemnym kierunku osi 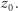 W układzie
W układzie 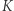 rozważany proces opisuje się następująco: ciało
rozważany proces opisuje się następująco: ciało 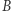 porusza się w dodatnim kierunku osi
porusza się w dodatnim kierunku osi  z prędkością o wartości
z prędkością o wartości  Kierunki dwóch pakietów falowych w układzie
Kierunki dwóch pakietów falowych w układzie 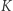 tworzą z osią
tworzą z osią 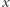 kąt
kąt 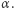 Zgodnie z prawem aberracji, w pierwszym przybliżeniu zachodzi związek:
Zgodnie z prawem aberracji, w pierwszym przybliżeniu zachodzi związek: 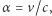 gdzie
gdzie  - prędkość światła. Z rozważań dotyczących przebiegu procesu w układzie
- prędkość światła. Z rozważań dotyczących przebiegu procesu w układzie 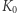 wiemy, że prędkość ciała
wiemy, że prędkość ciała 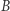 po pochłonięciu pakietów falowych
po pochłonięciu pakietów falowych 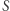 i
i 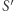 nie ulegnie zmianie.
nie ulegnie zmianie.
Zastosujemy teraz do naszego układu prawo zachowania pędu dla składowych w kierunku  w układzie
w układzie 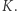
I. Niech 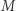 oznacza masę ciała
oznacza masę ciała 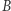 do chwili pochłonięcia pakietów falowych; w takim razie
do chwili pochłonięcia pakietów falowych; w takim razie 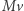 jest pędem ciała
jest pędem ciała 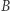 (zgodnie z mechaniką klasyczną). Każdy pakiet falowy ma energię
(zgodnie z mechaniką klasyczną). Każdy pakiet falowy ma energię 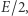 a więc - zgodnie ze znanym wnioskiem z teorii Maxwella - jego pęd ma wartość
a więc - zgodnie ze znanym wnioskiem z teorii Maxwella - jego pęd ma wartość 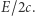 Ściśle rzecz biorąc, tyle jest równy pęd pakietu falowego
Ściśle rzecz biorąc, tyle jest równy pęd pakietu falowego 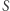 względem układu odniesienia
względem układu odniesienia 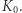 Kiedy jednak prędkość
Kiedy jednak prędkość  jest mała w porównaniu z
jest mała w porównaniu z 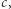 wówczas pęd w układzie
wówczas pęd w układzie 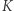 ma taką samą wartość - z dokładnością do wielkości małej drugiego rzędu (
ma taką samą wartość - z dokładnością do wielkości małej drugiego rzędu ( 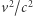 w porównaniu z 1). Wartość składowej tego pędu wzdłuż osi
w porównaniu z 1). Wartość składowej tego pędu wzdłuż osi  jest równa
jest równa 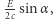 albo - z wystarczającą dokładnością (jeśli pominąć wielkości małe wyższych rzędów) -
albo - z wystarczającą dokładnością (jeśli pominąć wielkości małe wyższych rzędów) - 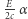 lub
lub 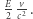 Zatem składowe pędów pakietów falowych
Zatem składowe pędów pakietów falowych 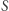 i
i 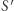 wzdłuż osi
wzdłuż osi  są w sumie równe
są w sumie równe 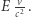 Tak więc pęd całkowity układu przed aktem pochłonięcia jest równy
Tak więc pęd całkowity układu przed aktem pochłonięcia jest równy
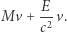 |
II. Niech 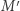 oznacza masę ciała
oznacza masę ciała 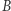 po akcie pochłonięcia. Z góry bierzemy tu pod uwagę możliwość zwiększenia masy po pochłonięciu energii
po akcie pochłonięcia. Z góry bierzemy tu pod uwagę możliwość zwiększenia masy po pochłonięciu energii 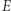 (jest to konieczne, aby ostateczny wynik naszych obliczeń był niesprzeczny). Wobec tego pęd układu po akcie pochłonięcia będzie równy
(jest to konieczne, aby ostateczny wynik naszych obliczeń był niesprzeczny). Wobec tego pęd układu po akcie pochłonięcia będzie równy
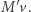 |
Skorzystamy wreszcie z zasady zachowania pędu dla składowych wzdłuż osi 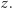 Daje to związek
Daje to związek
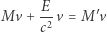 |
lub
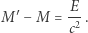 |
Związek ten wyraża prawo równoważności energii i masy. Zwiększenie energii o 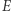 wiąże się ze wzrostem masy o
wiąże się ze wzrostem masy o 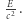 A wobec tego, że energię określa się zazwyczaj z dokładnością do stałej addytywnej, więc tę ostatnią możemy wybrać tak, aby zachodził związek:
A wobec tego, że energię określa się zazwyczaj z dokładnością do stałej addytywnej, więc tę ostatnią możemy wybrać tak, aby zachodził związek:
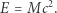 |
