Analizując proste zjawisko fizyczne, jakim było zderzenie dwóch cząstek, odtworzyliśmy tym samym nierówność Schwarza dla (dowolnych!) liczb nieujemnych 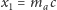, , 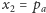, 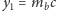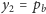(nieujemność liczb w nierówności Schwarza 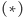 oczywiście nie uszczupla jej ogólności). Spróbujmy jeszcze spojrzeć na końcowy wynik (3) nieco ogólniej. W szczególnej teorii względności bardzo wygodnym pojęciem jest tzw.  czterowektor energii-pędu. Formalnie, dla poruszającej się cząstki o masie 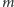 z pędem 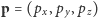i całkowitej energii 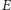 , jej czterowektor energii-pędu definiujemy jako uporządkowaną czwórkę 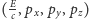i w skrócie piszemy 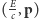. Jest to pojęcie analogiczne do pojęcia czterowektora położenia cząstki 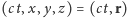. Takie czterowektory można mnożyć skalarnie. Żeby jednak iloczyn skalarny miał sensowne własności, nie powinien zmieniać się przy przekształceniach niezmieniających fizycznego sensu teorii, tzw. przekształceniach symetrii. W naszym przypadku przekształceniem symetrii jest transformacja Lorentza, a niezmienniczy iloczyn skalarny definiuje się następująco:

gdzie 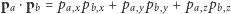oznacza już zwykły iloczyn skalarny w przestrzeni trójwymiarowej. Zauważmy, że wówczas długość czterowektora to po prostu

Zobaczmy, że (3) jest równoważna nierówności

a w języku czterowektorów i ich iloczynów skalarnych – nierówności

Zatem uzyskany główny wynik (3) jest niczym innym jak nierównością Schwarza dla czterowektorów energii-pędu cząstek 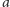 i 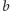 ! Tyle że zwrot tej nierówności jest w przeciwną stronę w stosunku do klasycznej nierówności Schwarza, co wynika ze szczególnej postaci iloczynu skalarnego. 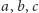Stwierdzenie, że zachodzi (3), można więc wyprowadzić bez żadnych, czynionych przez nas pracowicie, rozważań kinematycznych dla cząstek , po prostu powołując się na (4). Nierówność Schwarza (4) jest z kolei, jak widzieliśmy, naturalną konsekwencją tego, że iloczyn skalarny czterowektorów ma dobry sens fizyczny.

Dla autora przedstawione powyżej odkrycie nierówności w prawach fizyki było wstrząsającym i jednocześnie bardzo radosnym przeżyciem. Może Czytelnik zna fizyczny dowód jakiejś innej klasycznej nierówności?