Jak to działa?
Nierówność Schwarza a fizyka cząstek elementarnych
Czytelnik z pewnością zetknął się z tytułową nierównością Schwarza,
która w najprostszym przypadku mówi, że dla liczb rzeczywistych
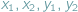 zachodzi
zachodzi
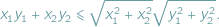 | (*) |
Interpretacja geometryczna jest jasna. Chodzi o to, że iloczyn skalarny dwóch
wektorów
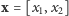 ,
,
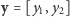 na płaszczyźnie, który
wynosi
na płaszczyźnie, który
wynosi
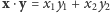 , nie przekracza iloczynu ich długości,
bowiem można wartość iloczynu skalarnego obliczyć także jako
, nie przekracza iloczynu ich długości,
bowiem można wartość iloczynu skalarnego obliczyć także jako
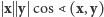 .
.
Często twierdzenia matematyczne mają także przyjemną interpretację
fizyczną (np. wiele twierdzeń z rachunku różniczkowego i całkowego).
Okazuje się, że nierówność Schwarza
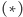 jest zaszyta, jak za chwilkę
zobaczymy, dosyć głęboko w elementarnych prawach mikroświata
i relatywistycznych prędkości.
jest zaszyta, jak za chwilkę
zobaczymy, dosyć głęboko w elementarnych prawach mikroświata
i relatywistycznych prędkości.
Rozważmy cząstkę elementarną
 , która rozpada się na dwie cząstki
, która rozpada się na dwie cząstki
 i
i
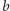 , poruszające się w przeciwne strony w ich układzie środka
masy (np. kaon rozpadający się na parę pionów
, poruszające się w przeciwne strony w ich układzie środka
masy (np. kaon rozpadający się na parę pionów
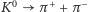 ). Wobec
tego, że cząstka
). Wobec
tego, że cząstka
 spoczywa, jest intuicyjnie jasne, że masy cząstek
spełniają nierówność
spoczywa, jest intuicyjnie jasne, że masy cząstek
spełniają nierówność

Rzeczywiście, analizując bilans energii w układzie środka masy, stwierdzamy,
że energia układu przed reakcją wynosiła
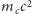 , po reakcji zaś
, po reakcji zaś

skąd

Ale jak wygląda sytuacja z naszej perspektywy, czyli w układzie laboratorium (w skrócie LAB)? Z transformacji Lorentza mamy

stąd

skąd

Wracając, mamy nierówność

Uwzględniając, że

podnosząc ostatnią nierówność stronami do kwadratu, skracając obustronnie
przez
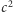 i upraszczając, dostajemy
i upraszczając, dostajemy
