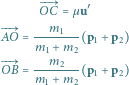Podobną konstrukcję można wykorzystać przy analizie sprężystego zderzenia dwóch cząstek. Dla uproszczenia załóżmy, że ich masy są jednakowe.
Prędkości cząstek przed zderzeniem będziemy oznaczać przez 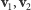 ,a po zderzeniu 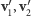 . Zasady zachowania energii i pędu będą miały postać:

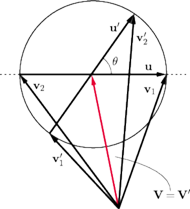
Rys. 2 Sprężyste zderzenie dwóch cząstek w języku prędkości względnej i prędkości środka masy.

Najwygodniej będzie wprowadzić nowe zmienne, określające prędkość środka masy układu i względną prędkość ciał

oraz analogiczne wielkości po zderzeniu 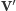  i 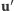 . Zasady zachowania przyjmą teraz niezwykle prostą postać

czyli wektor 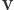jest niezmiennikiem zderzenia, a wektor 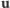 nie zmienia swojej długości (może jedynie zmienić kierunek), co jest zgodne z intuicją. Podobnie jak poprzednio, można to wygodnie zilustrować rysunkiem 2. W tym przypadku zderzenie sprowadza się wyłącznie do obrotu wektora 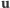 wpisanego w okrąg o promieniu  . Rozumowanie to można uogólnić na przypadek, gdy masy cząstek są różne. Weźmy dwie cząstki poruszające się jak poprzednio, ale o masach 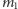 i 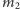 . Wprowadzając prędkość względną 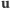 i prędkość środka masy

znajdujemy prędkości cząstek w układzie środka masy:

Z zasady zachowania pędu wiemy, że pędy cząstek w układzie środka masy po zderzeniu są równe i przeciwnie skierowane, z zasady zachowania energii wynika natomiast, że wartości bezwzględne prędkości nie zmieniają się, jedynie zmienia się kierunek (odpowiada to obrotowi na rysunku 2). Możemy w łatwy sposób przejść do układu laboratoryjnego, dodając do każdej z wyliczonych prędkości prędkość 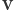 środka masy:

Do geometrycznej interpretacji wygodnie jest posłużyć się pędami cząstek. Zdefiniujmy wektor jednostkowy 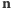 w kierunku 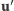 . Łatwo można przekonać się, że

gdzie wprowadziliśmy masę zredukowaną

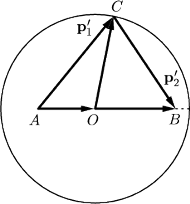
Rys. 3 Ta sama geometria, ale rysujemy pędy:

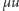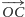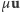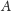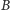Rozważmy więc okrąg o promieniu (rysunek 3). Wektor odpowiada wektorowi  , zatem powyższe równania można zinterpretować czysto geometrycznie jako dodawanie wektorów. Przy ustalonych początkowych pędach promień koła i położenia punktów  i  nie zmieniają się, natomiast punkt 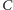 może swobodnie wędrować po okręgu. Rozważmy szczegółowo przypadek, gdy jedna z cząstek spoczywa (np. ta o masie 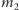 ). Zatem 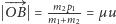i odcinek 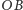pokrywa się z promieniem okręgu. Wektor 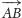pokrywa się, oczywiście, z pędem cząstki o masie 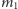 przed zderzeniem. W zależności od stosunku mas punkt 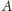 może leżeć wewnątrz lub na zewnątrz okręgu, jak na rysunku 4. Po zderzeniu obie cząstki doznają odchylenia od kierunku pierwotnego ruchu cząstki-pocisku, danego przez kąty 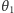 i  . 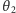W układzie środka masy kąt środkowy 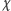 wyznacza kierunek, pod jakim zostaje rozproszona nadlatująca cząstka. Ciekawym ćwiczeniem dla Czytelnika może być przekonanie się na podstawie tych rysunków, że kąty 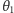 i 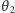 mogą być wyrażone przez kąt  :

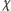Ponadto zauważmy, że kąt rozrzutu cząstek 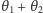może być mniejszy lub większy od 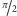 , w zależności od stosunku mas. Rozpraszanie do tyłu odpowiada równości .

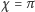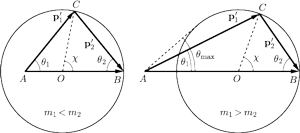
Rys. 4 Zderzenie pocisku ze spoczywającą cząstką.

Pokazaliśmy, że zjawiska mechaniczne zderzeń ciał mogą mieć bardzo łatwą interpretację geometryczną, a tworzenie takich diagramów jest samo w sobie interesujące. Szczególnie prosto można za pomocą tego narzędzia ustalać pewne zależności między wielkościami mierzonymi w układzie środka masy a ich odpowiednikami w układzie laboratoryjnym.

Na deser zostawmy kilka pytań/propozycji do zabawy:

1.

Dla jakiej wartości kąta 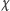 cząstka pierwotnie spoczywająca będzie miała największą energię? Jaka będzie jej wartość, jeśli energia cząstki padającej wynosi  ?

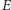2.

Dla 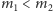prędkość pierwszej cząstki po zderzeniu może mieć dowolny kierunek. Jaka jest maksymalna wartość kąta 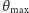 (wyrażona przez masy cząstek) w przypadku ?

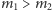3.

Pod jakim kątem rozbiegają się cząstki w przypadku równych mas? Jakie są wtedy 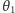 i  ?

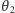4.

Ambitniejsze zadanie: jak przetłumaczyć przedstawione schematy na przypadek zderzeń niesprężystych, gdy zderzenie charakteryzuje pewien współczynnik strat energii ( , )?

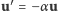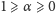5.

I jeszcze jedno zadanie dla odważnych. Jak zmienią się wyniki omawiane w tym artykule, jeśli uwzględnić efekty relatywistyczne?