Ograniczmy rozważania do geometrycznego spojrzenia na elastyczne zderzenie punktowych cząstek, wprowadzając zabawne i ciekawe narzędzie do analizy zderzeń. Sprowadzi się to do rysowania kółek i strzałek.

Rozważmy spoczywającą cząstkę o masie 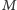 , która rozpada się samorzutnie na dwie nowe cząstki o równych masach 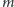 . Cząstki te poruszają się zatem z równymi prędkościami. Zajmijmy się jedną z nich – niech jej prędkość w układzie spoczywającej cząstki 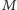 wynosi 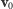 . Prędkość drugiej wynosi, oczywiście,  .

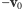Czytelnik Wnikliwy zauważy zapewne, że w opisanej tu sytuacji nie jest zachowana całkowita energia, ani całkowita masa! Energia potencjalna wszystkich składników układu jest stale równa zeru, energia kinetyczna cząstki przed rozpadem także równa się zeru, a energia kinetyczna produktów rozpadu to 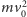 . Ten pozorny paradoks wynika z zaniedbania efektów relatywistycznych, tj. równoważności masy i energii.

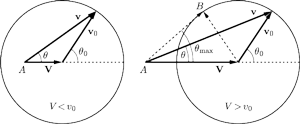
Rys. 1 Geometryczna interpretacja rozpadu cząstki.

Przejdźmy teraz do układu laboratoryjnego, w którym cząstka 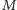 porusza się z prędkością 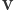 , pierwsza zaś z cząstek  z prędkością  . Prędkość ta jest, oczywiście, wektorową sumą prędkości w układzie pierwotnej cząstki i prędkości tego układu odniesienia w laboratorium:

Przepisując tę równość w postaci 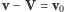i stosując twierdzenie cosinusów, otrzymamy związek

gdzie 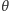jest kątem między wektoram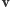i  i 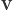 . Możemy posłużyć się bardzo wygodnym rysunkiem 1 do zobrazowania tej sytuacji. Prędkość  jest wektorempoprowadzonym do dowolnego punktu na obwodzie okręgu z punktu 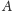 , odległego od środka okręgu o wektor 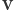 . Promień okręgu jest równy 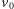 . Możemy przy tym rozróżnić dwa przypadki. Jeżeli 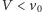, czyli punkt 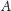 leży wewnątrz okręgu, to kąt 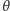 , pod jakim cząstka opuści układ, jest dowolny. W przypadku 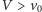cząstka może wylecieć tylko do przodu i pod kątem nieprzekraczającym 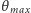 . Z konstrukcji przedstawionej na rysunku łatwo można przekonać się, że wartość kąta granicznego określa równość

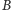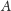Kąt ten odpowiada bowiem stycznej do okręgu w punkcie  , poprowadzonej z  . Takie kąty mierzy, oczywiście, obserwator w układzie laboratoryjnym. Rysunki te mają jeszcze jedną zaletę – możemy łatwo powiązać kąty w układzie środka masy z kątami mierzonymi w układzie laboratoryjnym. Pozostawiając przekształcenia Czytelnikowi, podajemy wynik